Bài tập minh họa Lập bảng xét dấu biểu thức chứa nhị thức bậc nhất

Dạng toán Lập bảng xét dấu biểu thức chứa nhị thức bậc nhất.
Ví dụ 1 . Lập bảng xét dấu các biểu thức sau:
a) $-2x+3.$
b) $4x-12.$
c) ${{x}^{2}}-4.$
d) $-2{{x}^{2}}+5x-2.$

a) Ta có $-2x+3=0$ $ \Leftrightarrow x=\frac{3}{2}$, $a=-2<0.$
Bảng xét dấu:

b) Ta có $4x-12=0$ $\Leftrightarrow x=3$, $a=4>0.$
Bảng xét dấu:

c) Ta có:
${{x}^{2}}-4=\left( x-2 \right)\left( x+2 \right).$
$x-2=0$ $ \Leftrightarrow x=2.$
$x+2=0$ $\Leftrightarrow x=-2.$
Bảng xét dấu:

d) Ta có: $-2{{x}^{2}}+5x-2=0\Leftrightarrow \left[ \begin{matrix}
x=2 \\
x=\frac{1}{2} \\
\end{matrix} \right.$
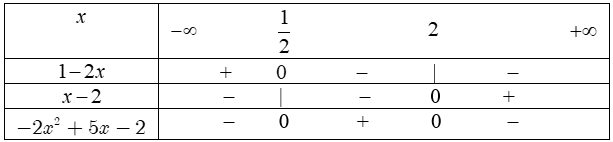
Suy ra $-2{{x}^{2}}+5x-2$ $=-2\left( x-2 \right)\left( x-\frac{1}{2} \right)$ $=\left( x-2 \right)\left( 1-2x \right).$
Bảng xét dấu:

Ví dụ 2 . Lập bảng xét dấu các biểu thức sau:
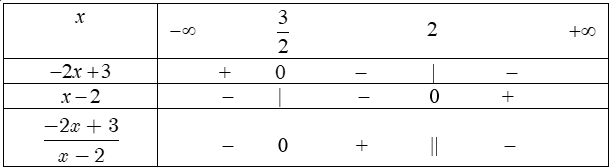
a) $\frac{-2x+3}{x-2}.$
b) $\frac{4x-12}{{{x}^{2}}-4x}.$
c) $x\left( 4-{{x}^{2}} \right)(x+2).$
d) $1-\frac{4{{x}^{2}}}{{{\left( x+1 \right)}^{2}}}.$

a) Bảng xét dấu:

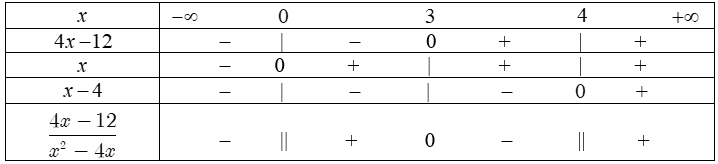
b) Ta có: $\frac{{4x – 12}}{{{x^2} – 4x}}$ $ = \frac{{4x – 12}}{{x\left( {x – 4} \right)}}.$
Bảng xét dấu:

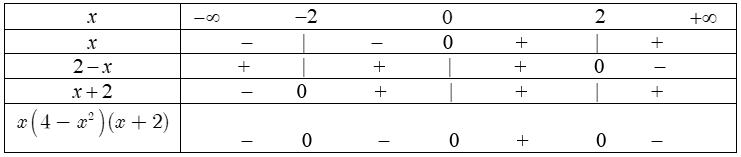
c) Ta có: $x\left( {4 – {x^2}} \right)(x + 2)$ $ = x\left( {2 – x} \right){\left( {x + 2} \right)^2}.$
Bảng xét dấu:

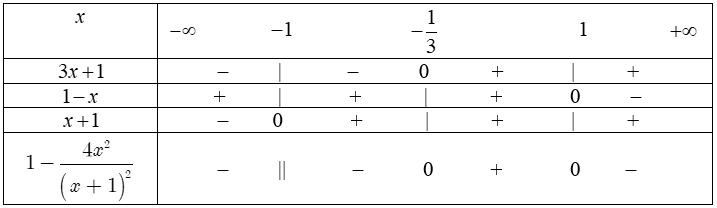
d) Ta có: $1 – \frac{{4{x^2}}}{{{{\left( {x + 1} \right)}^2}}}$ $ = \frac{{{{\left( {x + 1} \right)}^2} – 4{x^2}}}{{{{\left( {x + 1} \right)}^2}}}$ $ = \frac{{\left( {3x + 1} \right)\left( {1 – x} \right)}}{{{{\left( {x + 1} \right)}^2}}}.$
Bảng xét dấu:

Ví dụ 3 . Tùy vào $m$ xét dấu các biểu thức sau $\frac{-2x+m}{x-2}.$

a) Ta có:
$x-2=0$ $\Leftrightarrow x=2.$
$-2x+m=0$ $\Leftrightarrow x=\frac{m}{2}.$
Trường hợp 1: $\frac{m}{2}>2$ $\Leftrightarrow m>4.$
Bảng xét dấu:

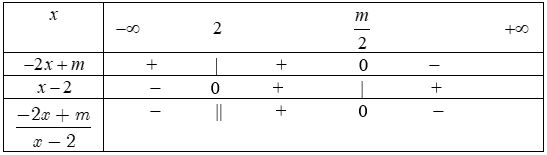
Suy ra $\frac{-2x+m}{x-2}>0$ $\Leftrightarrow x\in \left( 2;\frac{m}{2} \right)$ và $\frac{-2x+m}{x-2}<0$ $\Leftrightarrow x\in \left( -\infty ;2 \right)\cup \left( \frac{m}{2};+\infty \right).$
Trường hợp 2: $\frac{m}{2}=2$ $\Leftrightarrow m=4.$
Ta có $\frac{-2x+m}{x-2}=\frac{-2x+2}{x-2}=-2.$
Suy ra $\frac{-2x+m}{x-2}<0$ $\Leftrightarrow x\in \mathbb{R}\backslash \left\{ 2 \right\}.$
Trường hợp 3: $\frac{m}{2}<2$ $\Leftrightarrow m<4.$
Bảng xét dấu:

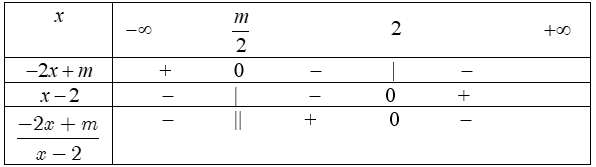
Suy ra $\frac{-2x+m}{x-2}>0$ $\Leftrightarrow x\in \left( \frac{m}{2};2 \right)$ và $\frac{-2x+m}{x-2}<0$ $\Leftrightarrow x\in \left( -\infty ;\frac{m}{2} \right)\cup \left( 2;+\infty \right).$