Đề thi mẫu HK1 Toán lớp 7 – số 4
— 13 —
Đề bài
PHẦN I. TRẮC NGHIỆM (2 điểm) Trả lời câu hỏi bằng cách viết lại chữ cái trước đáp án đúng vào bài làm:
Câu 1 : Kết quả phép tính \(\dfrac{{ – 5}}{{12}} + \dfrac{{ – 1}}{4}\) bằng
A. \(\dfrac{{ – 1}}{2}\) B. \(\dfrac{{ – 2}}{3}\)
C. \(\dfrac{1}{2}\) D. \(\dfrac{2}{3}\)
Câu 2 : Giá trị của x thỏa mãn đẳng thức \({x^3} = – 27\) là
A. \(x = 2\) B. \(x = – 2\)
C. \(x = 3\) D. \(x = – 3\)
Câu 3 : Nếu 15 lít dầu nặng 12kg thì 24kg dầu đó sẽ chứa vừa đầy trong thùng
A. 30 lít B. 27 lít
C. 15 lít D. 13,5 lít
Câu 4 : Cho x và y tỉ lệ thuận với nhau và khi \(x = – 3\)thì \(y = 12\). Hệ số tỉ lệ k của y đối với x là
A. \(k = – 0,25\) B. \(k = – 4\)
C. \(k = 0,25\) D. \(k = 4\)
Câu 5 : Biết rằng \(\dfrac{{ – 3}}{4} = \dfrac{x}{5}\). Khi đó giá trị của x là
A. \(\dfrac{{ – 15}}{4}\) B. \(\dfrac{{ – 20}}{3}\)
C. \( – 2\) D. \(2\)
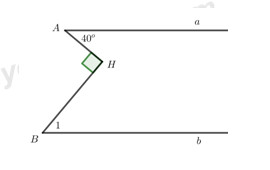
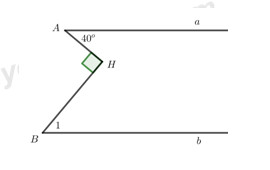
Câu 6 : Cho hình vẽ bên, biết đường thẳnga // b.
Khi đó số đo góc \({B_1}\) là
A. \({40^o}\) B. \({50^o}\)
C. \({130^o}\) D. \({140^o}\)
Câu 7 : Cho đường thẳng a cắt hai đường thẳng phân biệt b, c. Số cặp góc đồng vị được tạo ra là
A. 2 B. 3
C. 4 D. 6
Câu 8 : Trong các khẳng định sau khẳng định nào sai ?
A. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong cùng phía bù nhau.
B. Cho a, b, c là 3 đường thẳng phân biệt. Nếu \(a \bot b\) và \(b \bot c\) thì \(a\) // \(c\).
C. Mỗi góc ngoài của một tam giác bằng tổng hai góc trong của tam giác đó.
D. Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.
PHẦN II. TỰ LUẬN (8 điểm)
Câu 1 (2,5 điểm): Thực hiện phép tính:
a) \(\dfrac{7}{6} – \dfrac{1}{6}:\dfrac{2}{3}\)
b) \(1\dfrac{3}{4}.\dfrac{2}{7} – 1\dfrac{3}{4}.\dfrac{5}{7}\)
c)\(0,5\sqrt {100} – \dfrac{1}{4}\sqrt {16} + {\left( {\dfrac{{ – 2}}{3}} \right)^2}\)
Câu 2(1,5điểm): Ba lớp 7A, 7B, 7C trồng được 180 cây. Tính số cây mỗi lớp trông được, biết rằng số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5.
Câu 3 (3điểm): Cho đoạn thẳng AB. Qua trung điểm M của đoạn thẳng AB vẽ đường thẳng xy vuông góc với AB. Trên tia Mx lấy điểm C và D sao cho điểm C nằm giữa M và D.
a) Chứng minh \(\Delta AMC = \Delta BMC\).
b) Chứng minh \(\Delta ADC = \Delta BDC\).
c) Trên tia My lấy điểm E. Chứng minh \(\angle DAE = \angle DBE\).
Câu 4 (1 điểm): So sánh \(\sqrt 8 + \sqrt {15} \) và \(\sqrt {65} – 1\)
Lời giải chi tiết
I. TRẮC NGHIỆM
|
1. B |
2. D |
3. A |
4. B |
|
5. A |
6. B |
7. C |
8. C |
II. TỰ LUẬN
Câu 1:
Thực hiện phép tính:
a) \(\dfrac{7}{6} – \dfrac{1}{6}:\dfrac{2}{3} = \dfrac{7}{6} – \dfrac{1}{6}.\dfrac{3}{2} \\= \dfrac{7}{6} – \dfrac{1}{4} = \dfrac{{7.2 – 1.3}}{{12}} = \dfrac{{11}}{{12}}\)
b) \(1\dfrac{3}{4}.\dfrac{2}{7} – 1\dfrac{3}{4}.\dfrac{5}{7} = \dfrac{7}{4}.\dfrac{2}{7} – \dfrac{7}{4}.\dfrac{5}{7} \\= \dfrac{2}{4} – \dfrac{5}{4} = – \dfrac{3}{4}\)
c) \(0,5\sqrt {100} – \dfrac{1}{4}\sqrt {16} + {\left( {\dfrac{{ – 2}}{3}} \right)^2} \)
\(= 0,5.10 – \dfrac{1}{4}.4 + \dfrac{4}{9} = 5 – 1 + \dfrac{4}{9}\)
\(= 4 + \dfrac{4}{9} = \dfrac{{4.9 + 4}}{9} = \dfrac{{40}}{9}\)
Câu 2:
Ba lớp 7A, 7B, 7C trồng được 180 cây. Tính số cây mỗi lớp trông được, biết rằng số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5.
Gọi số cây ba lớp 7A, 7B, 7C trồng được lần lượt là x, y, z(cây) (\(x,y,z \in {N^*}\))
Ba lớp 7A, 7B, 7C trồng được 180 cây nên \(x + y + z = 180\)
Số cây của các lớp trên theo thứ tự tỉ lệ với 3; 4; 5 nên ta có:
\(x:y:z = 3:4:5\)
\(\Leftrightarrow \dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5} = \dfrac{{x + y + z}}{{3 + 4 + 5}} = \dfrac{{180}}{{12}} = 15\) (Áp dụng tính chất dãy tỉ số bằng nhau)
\( \Rightarrow x = 15.3 = 45\,\,\)(cây) \(;\,\,y = 15.4 = 60\) (cây) \(;\,\,z = 15.5 = 75\) (cây)
Vậy lớp 7A trồng 45 cây, lớp 7B trồng được 60 cây, lớp 7C trồng được 75 cây.
Câu 3:
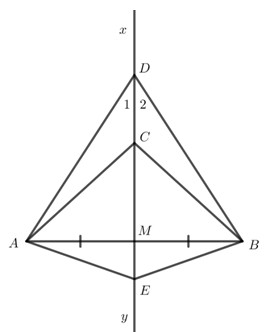
Cho đoạn thẳng AB. Qua trung điểm M của đoạn thẳng AB vẽ đường thẳng xy vuông góc với AB. Trên tia Mx lấy điểm C và D sao cho điểm C nằm giữa M và D.
a) Chứng minh \(\Delta AMC = \Delta BMC\) .
Ta có Mlà trung điểm của đoạn thẳng AB (gt)
\( \Rightarrow MA = MB\)
Xét \(\Delta AMC\) và \(\Delta BMC\) có:
MCchung; \(\angle AMC = \angle BMC = {90^o}\) (\(xy \bot AB\)); \(MA = MB\) (cmt)
\( \Rightarrow \)\(\Delta AMC = \Delta BMC\) (c.g.c)
b) Chứng minh \(\Delta ADC = \Delta BDC\).
Ta có \(\Delta AMC = \Delta BMC\) (cmt) \( \Rightarrow AC = BC\) (2 cạnh tương ứng)
Xét \(\Delta AMD\) và \(\Delta BMD\) có:
MDchung; \(\angle AMD = \angle BMD = {90^o}\) (\(xy \bot AB\)); \(MA = MB\) (cmt)
\( \Rightarrow \)\(\Delta AMD = \Delta BMD\) (c.g.c) \( \Rightarrow AD = BD\) (2 cạnh tương ứng)
Xét \(\Delta ADC\) và \(\Delta BDC\) có:
DCchung; \(AC = BC\) (cmt); \(AD = BD\) (cmt)
\( \Rightarrow \)\(\Delta ADC = \Delta BDC\) (c.c.c)
c) Trên tia My lấy điểm E. Chứng minh \(\angle DAE = \angle DBE\) .
Ta có\(\Delta ADC = \Delta BDC\) (cmt)\( \Rightarrow \angle {D_1} = \angle {D_2}\) (2 góc tương ứng)
Xét \(\Delta DAE\) và \(\Delta DBE\) có:
DEchung; \(\angle {D_1} = \angle {D_2}\) (cmt); \(AD = BD\) (cmt)
\( \Rightarrow \)\(\Delta DAE = \Delta DBE\) (c.g.c) \( \Rightarrow \angle DAE = \angle DBE\) (2 góc tương ứng)
Câu 4:
So sánh \(\sqrt 8 + \sqrt {15} \) và \(\sqrt {65} – 1\)
Ta có: \(\left\{ \begin{array}{l}\sqrt 8 < \sqrt 9 = 3\\\sqrt {15} < \sqrt {16} = 4\end{array} \right. \Rightarrow \sqrt 8 + \sqrt {15} < 3 + 4 = 7\)
Mặt khác: \(\sqrt {65} > \sqrt {64} = 8 \Rightarrow \sqrt {65} – 1 > 8 – 1 = 7\)
Vậy \(\sqrt 8 + \sqrt {15} < \sqrt {65} – 1\)
