Giải SGK Bài 4. Phương trình lượng giác cơ bản – Toán 11 CD

Đề bài

Giải phương trình

a)     \(\sin \left( {2x + \frac{\pi }{4}} \right) = \sin x\)

b)     \(\sin 2x = \cos 3x\)

c)     \({\cos ^2}2x = {\cos ^2}\left( {x + \frac{\pi }{6}} \right)\)

Sử dụng các công thức tổng quát để giải phương trình sin, cos

Lời giải chi tiết

a)

\(\sin \left( {2x + \frac{\pi }{4}} \right) = \sin x \Leftrightarrow \left[ \begin{array}{l}2x + \frac{\pi }{4} = x + k2\pi \\2x + \frac{\pi }{4} = \pi  – x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  – \frac{\pi }{4} + k2\pi \\3x = \pi  – \frac{\pi }{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  – \frac{\pi }{4} + k2\pi \\x = \frac{\pi }{4} + \frac{{k2\pi }}{3}\end{array} \right.;k \in Z\)

b)

\(\begin{array}{l}\sin 2x = \cos 3x\\ \Leftrightarrow \cos 3x = \cos \left( {\frac{\pi }{2} – 2x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}3x = \frac{\pi }{2} – 2x + k2\pi \\3x =  – \left( {\frac{\pi }{2} – 2x} \right) + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}5x = \frac{\pi }{2} + k2\pi \\x =  – \frac{\pi }{2} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{10}} + \frac{{k2\pi }}{5}\\x =  – \frac{\pi }{2} + k2\pi \end{array} \right.\end{array}\)

c)

\(\begin{array}{l}{\cos ^2}2x = {\cos ^2}\left( {x + \frac{\pi }{6}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\cos 2x = \cos \left( {x + \frac{\pi }{6}} \right)\\\cos 2x =  – \cos \left( {x + \frac{\pi }{6}} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos 2x = \cos \left( {x + \frac{\pi }{6}} \right)\\\cos 2x = \cos \left( {\pi  – \left( {x + \frac{\pi }{6}} \right)} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos 2x = \cos \left( {x + \frac{\pi }{6}} \right)\\\cos 2x = \cos \left( {\frac{{5\pi }}{6} – x} \right)\end{array} \right.\end{array}\)

Với \(\cos 2x = \cos \left( {x + \frac{\pi }{6}} \right) \Leftrightarrow \left[ \begin{array}{l}2x =  – \left( {x + \frac{\pi }{6}} \right) + k2\pi \\2x = x + \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3x =  – \frac{\pi }{6} + k2\pi \\x = \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  – \frac{\pi }{{18}} + \frac{{k2\pi }}{3}\\x = \frac{\pi }{6} + k2\pi \end{array} \right.\)

Với \(\cos 2x = \cos \left( {\frac{{5\pi }}{6} – x} \right) \Leftrightarrow \left[ \begin{array}{l}2x = \frac{{5\pi }}{6} – x + k2\pi \\2x =  – \left( {\frac{{5\pi }}{6} – x} \right) + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3x = \frac{{5\pi }}{6} + k2\pi \\x =  – \frac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\pi }}{{18}} + \frac{{k2\pi }}{3}\\x =  – \frac{{5\pi }}{6} + k2\pi \end{array} \right.\)

Đề bài

Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:

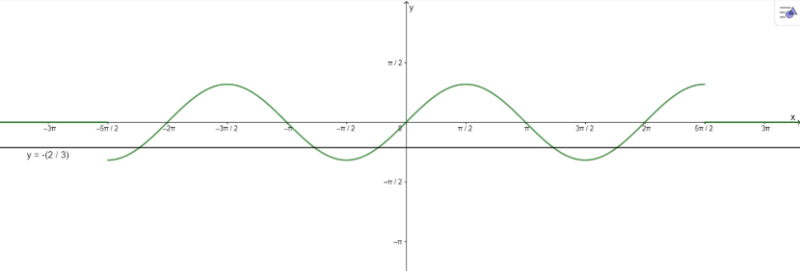
a)     \(3\sin x + 2 = 0\) trên đoạn \(\left( { – \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\)

b)     \(\cos x = 0\) trên đoạn \(\left[ { – \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\)

Dựa vào cách vẽ đồ thị đã học để xác định

Lời giải chi tiết

a)     Vẽ đồ thị:

\(3\sin x + 2 = 0\) trên đoạn \(\left( { – \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm

b)     Vẽ đồ thị:

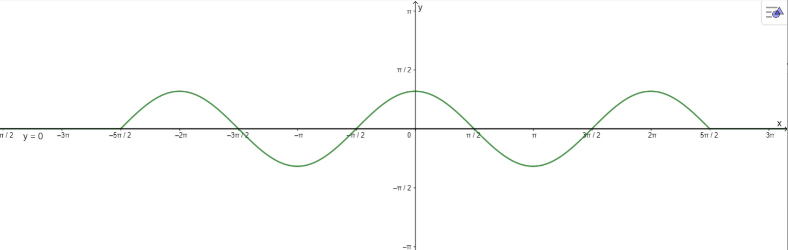
\(\cos x = 0\) trên đoạn \(\left[ { – \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm

Đề bài

Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ \(40^\circ \) Bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số:\(d\left( t \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] + 12\) với \(t \in \mathbb{Z}\,\,v\`a \,\,0 < t \le 365\)

a)     Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm?

b)     Vào ngày nào trong năm thì thành phố A có đúng 9 giờ có ảnh sáng mặt trời?

c)     Vào ngày nào trong năm thì thành phố A có đúng 15 giờ có ánh sáng mặt trời?

Sử dụng công thức tổng quát để giải phương trình hàm số sin

Lời giải chi tiết

a) Thành phố A có đúng 12 giờ có ánh sáng mặt trời thì d(t)=12

Khi đó

\(\begin{array}{l}12 = 3\sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] + 12\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] = 0\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] = \sin 0\\ \Leftrightarrow \frac{\pi }{{182}}\left( {t – 80} \right) = k\pi \\ \Leftrightarrow t = 80 + 182k;k \in Z\end{array}\)

Mà \(t \in \mathbb{Z}\) và \(0 < t \le 365\) nên

\(\begin{array}{l}0 < 80 + 182k \le 365\\ \Rightarrow 0 \le k \le 1,56\end{array}\)

Suy ra \(k \in \left\{ {0;1} \right\}\)

Khi đó \(t \in \left\{ {80;262} \right\}\)

Vậy Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 80 và 262 trong năm

b) Thành phố A có đúng 9 giờ có ánh sáng mặt trời thì d(t)=9

Khi đó

\(\begin{array}{l}9 = 3\sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] + 12\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] =  – 1\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] = \sin \left( { – \frac{\pi }{2}} \right)\\ \Leftrightarrow \frac{\pi }{{182}}(t – 80) =  – \frac{\pi }{2} + k\pi \\ \Leftrightarrow t =  – 11 + 182k;k \in Z\end{array}\)

Mà \(t \in \mathbb{Z}\) và \(0 < t \le 365\) nên

\(\begin{array}{l}0 <  – 11 + 182k \le 365\\ \Rightarrow 0 < k \le 2,07\end{array}\)

Suy ra \(k \in \left\{ {1;2} \right\}\)

Khi đó \(t \in \left\{ {71;353} \right\}\)

Vậy Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 71 và 353 trong năm

c) Thành phố A có đúng 15 giờ có ánh sáng mặt trời thì d(t)=15

Khi đó

\(\begin{array}{l}15 = 3\sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] + 12\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] = 1\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] = \sin \left( {\frac{\pi }{2}} \right)\\ \Leftrightarrow \frac{\pi }{{182}}(t – 80) = \frac{\pi }{2} + k\pi \\ \Leftrightarrow t = 171 + 182k;k \in Z\end{array}\)

Mà \(t \in \mathbb{Z}\) và \(0 < t \le 365\) nên

\(\begin{array}{l}0 < 171 + 182k \le 365\\ \Rightarrow 0 \le k \le 1,06\end{array}\)

Suy ra \(k \in \left\{ {0;1} \right\}\)

Khi đó \(t \in \left\{ {171;353} \right\}\)

Vậy Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 171 và 353 trong năm

Đề bài

Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 39). Nghiên cứu trò chơi này, người ta thấy khoảng cách h (m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian t (s) (với \(t \ge 0\)) bởi hệ thức \(h = \left| d \right|\) với \(d = 3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right]\), trong đó ta quy ước d > 0 khi vị trí cân bằng ở phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại. Vào thời gian t nào thì khoảng cách h là 3m; 0m?

Sử dụng công thức tổng quát để giải phương trình hàm số cos.

Lời giải chi tiết

+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 3m thì h = 3.

Khi đó

\(\begin{array}{l}3 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right]} \right|\\ \Rightarrow \left[ \begin{array}{l}3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 3\\3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] =  – 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 1\\\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] =  – 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = \cos 0\\\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = \cos \pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{3}\left( {2t – 1} \right) = k2\pi \\\frac{\pi }{3}\left( {2t – 1} \right) = \pi  + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{6k + 1}}{2}\\t = 3k + 2\end{array} \right.;k \in Z\end{array}\)

+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 0m thì h = 0.

Khi đó

\(\begin{array}{l}0 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right]} \right|\\ \Rightarrow 3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = \cos \frac{\pi }{2}\\ \Leftrightarrow \frac{\pi }{3}\left( {2t – 1} \right) = \frac{\pi }{2} + k\pi \\ \Leftrightarrow t = \frac{5}{4} + \frac{{3k}}{2};k \in Z\end{array}\)