Giải SBT Toán 6 tập 2 bài 3: Phép cộng, phép trừ phân số – Sách bài tập Cánh diều
=============
Câu 27. Tính các tổng sau (tính hợp lí nếu có thể):
a) $\frac{7}{-27}$ + $\frac{-8}{27}$
b) $\frac{6}{13}$ + $\frac{-17}{39}$
c) $\frac{-17}{13}$ + $\frac{25}{101}$ + $\frac{4}{13}$
d) $\frac{-13}{7}$ + $\frac{3}{5}$ + $\frac{-1}{7}$
e) $\frac{-5}{9}$ + $\frac{8}{15}$ + $\frac{4}{-9}$ + $\frac{7}{15}$
Trả lời:
a) $\frac{7}{-27}$ + $\frac{-8}{27}$ = $\frac{-7}{27}$ + $\frac{-8}{27}$ = $\frac{-15}{27}$ = $\frac{-5}{9}$
b) $\frac{6}{13}$ + $\frac{-17}{39}$ = $\frac{18}{39}$ + $\frac{-17}{39}$ = $\frac{1}{39}$
c) $\frac{-17}{13}$ + $\frac{25}{101}$ + $\frac{4}{13}$ = ($\frac{-17}{13}$ + $\frac{4}{13}$) + $\frac{25}{101}$ = -1 + $\frac{25}{101}$ = $\frac{-76}{101}$
d) $\frac{-13}{7}$ + $\frac{3}{5}$ + $\frac{-1}{7}$ = ($\frac{-13}{7}$ + $\frac{-1}{7}$) + $\frac{3}{5}$ = (-2) + $\frac{3}{5}$ = $\frac{-7}{5}$
e) $\frac{-5}{9}$ + $\frac{8}{15}$ + $\frac{4}{-9}$ + $\frac{7}{15}$ = ($\frac{-5}{9}$ + $\frac{-4}{9}$) + ($\frac{8}{15}$ + $\frac{7}{15}$) = (-1) + 1 = 0
Câu 28. So sánh các biểu thức:
a) A = $\frac{1}{2}$ + $\frac{-3}{8}$ + $\frac{5}{9}$ và B = $\frac{13}{-30}$ + $\frac{17}{45}$ + $\frac{-7}{18}$
b) C = $\frac{12}{25}$ + $\frac{-8}{15}$ + $\frac{-4}{9}$ và D = $\frac{-5}{12}$ + $\frac{4}{9}$ + $\frac{-11}{6}$
c) M = $\frac{1}{3}$ + $\frac{2}{-5}$ + $\frac{7}{2}$ và N = $\frac{19}{-7}$ + $\frac{21}{5}$ + $\frac{-2}{7}$
d) P = $\frac{34}{24}$ + $\frac{-8}{15}$ + $\frac{1}{10}$ và Q = $\frac{8}{21}$ + 1 + $\frac{1}{-21}$
Trả lời:
a) A = $\frac{1}{2}$ + $\frac{-3}{8}$ + $\frac{5}{9}$ = $\frac{49}{72}$
B = $\frac{13}{-30}$ + $\frac{17}{45}$ + $\frac{-7}{18}$ = $\frac{-4}{9}$
Vậy A > B
b) C = $\frac{12}{25}$ + $\frac{-8}{15}$ + $\frac{-4}{9}$ = $\frac{-112}{225}$
D = $\frac{-5}{12}$ + $\frac{4}{9}$ + $\frac{-11}{6}$ = $\frac{-65}{36}$
Vậy C > D
c) M = $\frac{1}{3}$ + $\frac{2}{-5}$ + $\frac{7}{2}$ = $\frac{103}{30}$
N = $\frac{19}{-7}$ + $\frac{21}{5}$ + $\frac{-2}{7}$ = $\frac{6}{5}$
Vậy N < M
d) P = $\frac{34}{24}$ + $\frac{-8}{15}$ + $\frac{1}{10}$ = $\frac{59}{60}$
Q = $\frac{8}{21}$ + 1 + $\frac{1}{-21}$ = $\frac{4}{3}$
Vậy P < Q
Câu 29. Không tính trực tiếp, chứng tỏ tổng của ba phân số sau: $\frac{20}{11}$; $\frac{20}{31}$; $\frac{20}{51}$ nhỏ hơn $\frac{7}{2}$
Trả lời:
Đặt A = $\frac{20}{11}$ + $\frac{20}{31}$ + $\frac{20}{51}$.
A < $\frac{20}{10}$ + $\frac{20}{30}$ + $\frac{20}{50}$ = 2 + $\frac{2}{3}$ + $\frac{2}{5}$ = $\frac{46}{15}$
Mà $\frac{46}{15}$ < $\frac{7}{2}$
Vậy A < $\frac{7}{2}$
Câu 30. Viết tên một giáo sư đoạt giải thưởng Toan học cao quý nhất thế giớ bằng cách thực hiện các yêu cầu sau: tính các tổng sau đây, rồi điền các chữ vào vị trí tương ứng với tổng vừa tính ở bảng sau:
C. $\frac{-4}{5}$ + $\frac{9}{7}$
N. $\frac{7}{21}$ + $\frac{9}{-36}$
O. 1 + $\frac{-1}{11}$
B. $\frac{11}{15}$ + $\frac{9}{-10}$
Ô. (-$\frac{18}{24}$) + $\frac{15}{-21}$
G. $\frac{-3}{10}$ + $\frac{7}{24}$
Ả. $\frac{1}{2}$ + ($\frac{-1}{3}$)
H. $\frac{-3}{21}$ + $\frac{6}{42}$
Â. 2 + $\frac{7}{-9}$
U. $\frac{2}{7}$ – $\frac{85}{77}$
| $\frac{1}{12}$ | $\frac{-1}{120}$ | $\frac{-41}{28}$ | $\frac{-1}{6}$ | $\frac{1}{6}$ | $\frac{10}{11}$ | $\frac{17}{35}$ | 0 | $\frac{11}{9}$ | $\frac{-9}{11}$ |
Trả lời:
C. $\frac{-4}{5}$ + $\frac{9}{7}$ = $\frac{17}{35}$
N. $\frac{7}{21}$ + $\frac{9}{-36}$ = $\frac{1}{12}$
O. 1 + $\frac{-1}{11}$ = $\frac{10}{11}$
B. $\frac{11}{15}$ + $\frac{9}{-10}$ = $\frac{-1}{6}$
Ô. (-$\frac{18}{24}$) + $\frac{15}{-21}$ = $\frac{-41}{28}$
G. $\frac{-3}{10}$ + $\frac{7}{24}$ = $\frac{-1}{120}$
Ả. $\frac{1}{2}$ + ($\frac{-1}{3}$) = $\frac{1}{6}$
H. $\frac{-3}{21}$ + $\frac{6}{42}$ = 0
Â. 2 + $\frac{7}{-9}$ = $\frac{11}{9}$
U. $\frac{2}{7}$ – $\frac{85}{77}$ = $\frac{-9}{11}$
| N | G | Ô | B | Ả | O | C | H | Â | U |
| $\frac{1}{12}$ | $\frac{-1}{120}$ | $\frac{-41}{28}$ | $\frac{-1}{6}$ | $\frac{1}{6}$ | $\frac{10}{11}$ | $\frac{17}{35}$ | 0 | $\frac{11}{9}$ | $\frac{-9}{11}$ |
Câu 31. Tìm số nguyên x, biết:
a) $\frac{-5}{7}$ + 1 + $\frac{30}{-7}$ $\leq $ $\frac{-1}{6}$ + $\frac{1}{3}$ + $\frac{5}{6}$;
b) $\frac{-8}{13}$ + $\frac{7}{17}$ + $\frac{21}{13}$ $\leq $ $\frac{-9}{14}$ +3 + $\frac{5}{-14}$
Trả lời:
a) Ta có: -4 $\leq $ x $\leq $ 1, x $\in $ Z, suy ra x $\in $ {-4; -3; -2; -1; 0; 1}
b) Ta có: $\frac{24}{17}\leq x\leq 2, x $\in $ Z suy ra x = 2
Câu 32. Tìm tổng các phân số đồng thời lớn hơn $\frac{-1}{2}$, nhỏ hơn $\frac{-1}{3}$ và có tử là 5
Trả lời:
Giả sử các phân số có dạng $\frac{5}{x}$ (x thuộc Z, x khác 0)
Ta có: $\frac{-1}{2}<\frac{5}{x}<\frac{-1}{3}$ suy ra $\frac{5}{-10}<\frac{5}{x}<\frac{5}{-15}$
Do đó -15 < x < -10
Vậy tổng các phân số cần tìm là:
$\frac{5}{-11}$ + $\frac{5}{-12}$ + $\frac{5}{-13}$ + $\frac{5}{-14}$ = $\frac{-19357}{12012}$
Câu 33. Ba ô tô cùng chuyển long nhãn từ một kho ở Hưng Yên lên Hà Nội. Ô tô thứ nhất, thứ hai, thứ ba chuyển được lần lượt $\frac{1}{3}$; $\frac{1}{5}$ và $\frac{2}{9}$ số long nhãn trong kho. Cả ba ô tô chuyển được bao nhiêu phần long nhãn trong kho?
Trả lời:
Cả ba ô tô chuyển được:
$\frac{1}{3}$ + $\frac{1}{5}$ + $\frac{2}{9}$ = $\frac{34}{45}$ (số long nhãn trong kho)
Câu 34. Người thứ nhất đi xe đạp từ A đến B hết 5 giờ; người thứ hai đi xe máy từ B về A hết 2 giờ; người thứ hai khởi hành sau người thứ nhất 2 giờ. Khỏi sau khi người thứ hai đi được 1 giờ thì hai người đã gặp nhau chưa?
Trả lời:
Trong 3 giờ người đi xe đạp đi được $\frac{3}{5}$ quãng đường.
Trong 1 giờ người đi xe máy đi được $\frac{1}{2}$ quãng đường.
Tổng số quãng đường hai người đã đi là:
$\frac{3}{5}$ + $\frac{1}{2}$ = $\frac{11}{10}$ (quãng đường)
Vì $\frac{11}{10}$ > 1 nên hai người đã gặp nhau
Câu 35. Một người hỏi Py-ta-go về số học trò của ông. Ông nói: “Một nửa số học trò của tôi đang học Toán, một phần tư đang học nhạc, một phần bảy đang ngồi suy nghĩ. Số còn lại là 3 người”. Ông có bao nhiêu học trò?
Trả lời:
Số học trò học Toán, học Nhạc và đang suy nghĩ là:
$\frac{1}{2}$ + $\frac{1}{4}$ + $\frac{1}{7}$ = $\frac{25}{28}$ (số học trò)
Suy ra $\frac{3}{28}$ số học trò tương ứng với 3 người.
Vậy số học trò của Py-ta-go là 28 người.
Câu 36. Có 5 quả cam chia đều cho 6 người. Làm thế nào để chia được mà không phải cắt bất kì quả cảm nào thành 6 phần bằng nhau.
Trả lời:
Nhận xét: $\frac{5}{6}$ = $\frac{1}{2}$ + $\frac{1}{3}$.
Do đó khi chia 5 quả cam cho 6 người thì mỗi người nhận được $\frac{5}{6}$ quả cam hay $\frac{1}{2}$ quả cam và $\frac{1}{3}$ quả cam.
Vậy để không phải cắt bất kì một quả cam nào thành 6 phần bằng nhau ta lấy 2 quả, mỗi quả chia thành 3 phần thì có đủ 6 phần cho mọi người, rồi lấy 3 quả mỗi quả chia đôi thì được 6 miếng bằng nhau chia đều cho 6 người.
Khi đó mỗi người nhận được : $\frac{1}{2}$ + $\frac{1}{3}$ = $\frac{5}{6}$ quả cam
Câu 37. Hoàn thành hai tháp số sau:
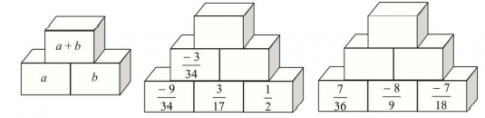
Trả lời:
Tham khảo:
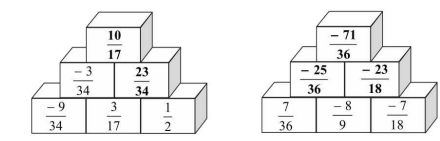
=============
[Sách cánh diều] Giải SBT Toán 6 — Giải SBT Toán 6 tập 2 cánh diều
