Giải SBT Bài cuối Chương 4 – SBT Toán 10 CHÂN TRỜI – GIẢI CHI TIẾT
===========
Giải bài 1 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Khẳng định nào sau đây là đúng?
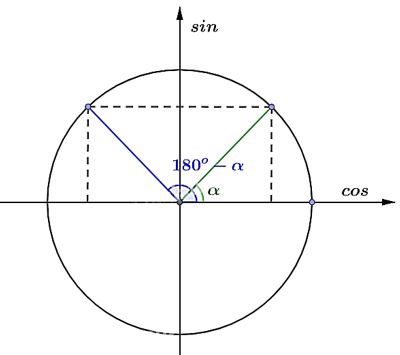
A. \(\sin \alpha = \sin \left( {180^\circ – \alpha } \right)\)
B. \(\cos \alpha = \cos \left( {180^\circ – \alpha } \right)\)
C. \(\tan \alpha = \tan \left( {180^\circ – \alpha } \right)\)
D. \(\cot \alpha = \cot \left( {180^\circ – \alpha } \right)\)
Phương pháp giải
Vẽ hình

Lời giải chi tiết
\(\sin \alpha = \sin \left( {180^\circ – \alpha } \right)\)
\(\cos \alpha = – \cos \left( {180^\circ – \alpha } \right)\)
Chọn A. \(\sin \alpha = \sin \left( {180^\circ – \alpha } \right)\)
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 2 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Trong các khẳng định sau đây, khẳng định nào sai?
A. \(\cos 45^\circ = \sin 45^\circ \)
B. \(\cos 45^\circ = \sin 135^\circ \)
C. \(\cos 30^\circ = \sin 120^\circ \)
D. \(\sin 60^\circ = \cos 120^\circ \)
Phương pháp giải
\(\cos \alpha = – \cos \left( {180^\circ – \alpha } \right)\)
\(\cos \alpha = \sin \left( {90^\circ – \alpha } \right)\)
Lời giải chi tiết
\(\cos 45^\circ = \sin \left( {90^\circ – 45^\circ } \right) = \sin 45^\circ = \sin \left( {180^\circ – 45^\circ } \right) = \sin 135^\circ \)
=> A, B đúng
\(\cos 30^\circ = \sin \left( {90^\circ – 30^\circ } \right) = \sin 60^\circ = \sin \left( {180^\circ – 60^\circ } \right) = \sin 120^\circ \), suy ra C đúng
Chọn D.
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 3 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Bất đẳng thức nào sau đây là bất đẳng thức đúng?
A. \(\sin 90^\circ < \sin 150^\circ \)
B. \(\sin 90^\circ 15′ < \sin 90^\circ 30’\)
C. \(\sin 90^\circ 30′ > \cos 100^\circ \)
D. \(\cos 150^\circ > \cos 120^\circ \)
Phương pháp giải
Có : \(\sin 90^\circ < \sin 150^\circ\)
Sử dụng máy tính cầm tay tính được kết quả rồi so sánh
Lời giải chi tiết
\(\sin 90^\circ < \sin 150^\circ \Leftrightarrow \sin 90^\circ – \sin 150^\circ < 0\)
Sử dụng máy tính cầm tay: \(\sin 90^\circ – \sin 150^\circ \) ta được kết quả là \(\frac{1}{2} > 0\) => A sai
Tương tự ta có: \(\sin 90^\circ 15′ – \sin 90^\circ 30′ = 0,000029 > 0\)=> B sai
\(\sin 90^\circ 30′ – \cos 100^\circ = 1,17 > 0\) => C đúng
Chọn C
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 4 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Trong các đẳng thức sau đây đẳng thức nào đúng?
A. \(\sin 150^\circ = – \frac{{\sqrt 3 }}{2}\)
B. \(\cos 150^\circ = \frac{{\sqrt 3 }}{2}\)
C. \(\tan 150^\circ = – \frac{1}{{\sqrt 3 }}\)
D. \(\cot 150^\circ = \sqrt 3 \)
Phương pháp giải
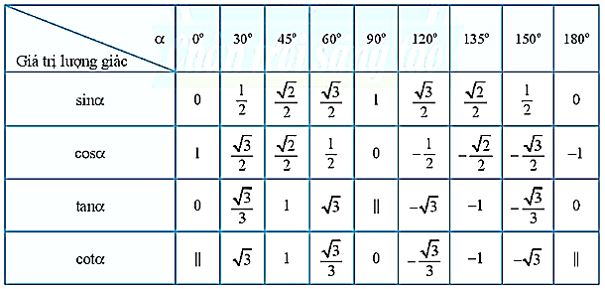
Lời giải chi tiết
Tra bảng giá trị lượng giác một số góc đặc biệt ta có \(\tan 150^\circ = – \frac{1}{{\sqrt 3 }}\)
Chọn C.
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 5 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Cho tam giác ABC có \(BC = a,CA = b,AB = c\). Mệnh đề nào sau đây đúng?
A. Nếu \({b^2} + {c^2} – {a^2} > 0\) thì góc A nhọn
B. Nếu \({b^2} + {c^2} – {a^2} > 0\) thì góc A tù
C. Nếu \({b^2} + {c^2} – {a^2} < 0\) thì góc A nhọn
D. Nếu \({b^2} + {c^2} – {a^2} < 0\) thì góc A vuông
Phương pháp giải
Áp dụng định lí côsin:
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} – 2bc\cos A\\{b^2} = {c^2} + {a^2} – 2ca\cos B\\{c^2} = {a^2} + {b^2} – 2ab\cos C\end{array}\)
Lời giải chi tiết
Áp dụng định lí côsin ta có: \(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}\)
Mà \(a,b,c > 0 \Rightarrow 2bc > 0\)
Nên dấu của \(\cos A\) phụ thuộc vào tử số \({b^2} + {c^2} – {a^2}\)
Ta có \(\begin{array}{l}0^\circ < \widehat A < 90^\circ \Rightarrow \cos A > 0\\90^\circ < \widehat A < 180^\circ \Rightarrow \cos A < 0\\\widehat A = 90^\circ \Rightarrow \cos A = 0\\\widehat A = 180^\circ \Rightarrow \cos A = – 1\end{array}\)
=> Nếu \({b^2} + {c^2} – {a^2} > 0\) thì góc A nhọn
Chọn A.
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 6 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Cho tam giác ABC có \(AB = 4\) cm, \(BC = 7\) cm, \(CA = 9\). Giá trị \(\cos A\) là
A. \(\frac{2}{3}\)
B. \(\frac{1}{3}\)
C. \(\frac{4}{5}\)
D. \(\frac{8}{9}\)
Phương pháp giải
Áp dụng định lí côsin:
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} – 2bc\cos A\\{b^2} = {c^2} + {a^2} – 2ca\cos B\\{c^2} = {a^2} + {b^2} – 2ab\cos C\end{array}\)
Lời giải chi tiết
Áp dụng định lí côsin ta có:
\(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{{{9^2} + {4^2} – {7^2}}}{{2.9.4}} = \frac{2}{3}\)
Chọn A
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 7 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Cho tam giác ABC có \(AB = 8\) cm, \(AC = 18\) cm và có diện tích bằng 64 cm2. Giá trị \(\sin A\) là:
A. \(\frac{{\sqrt 3 }}{2}\)
B. \(\frac{3}{8}\)
C. \(\frac{4}{5}\)
D. \(\frac{8}{9}\)
Phương pháp giải
Áp dụng định lí sin:
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\)
Lời giải chi tiết
Áp dụng định lí sin ta có:
\({S_{ABC}} = \frac{1}{2}AB.AC.\sin A \Rightarrow \sin A = \frac{{2{S_{ABC}}}}{{AB.AC}} = \frac{{2.64}}{{8.18}} = \frac{8}{9}\)
Chọn D
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 8 trang 80 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Cho tam giác ABC vuông cân tại A có \(AB = AC = 30\) cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích của tam giác GFC là:
A. 50 \(cm^2\)
B. \(50\sqrt 2 \) \(cm^2\)
C. 75 \(cm^2\)
D.\(15\sqrt {105} \) \(cm^2\)
Phương pháp giải
Tính: \( GF \Rightarrow {S_{\Delta GCF}}\), \(CF \Rightarrow {S_{\Delta BCF}}\)
\( \Rightarrow {S_{\Delta GCF}} = \frac{1}{6}{S_{\Delta ABC}}\)
Lời giải chi tiết
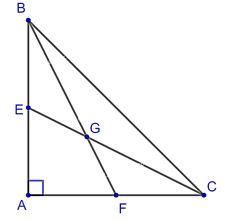
Ta có CE, BF là đường trung tuyến nên G là trọng tâm của tam giác ABC.
\( \Rightarrow GF = \frac{1}{3}BF \Rightarrow {S_{\Delta GCF}} = \frac{1}{3}{S_{\Delta BCF}}\)
Mà \(CF = \frac{1}{2}AC \Rightarrow {S_{\Delta BCF}} = \frac{1}{2}{S_{\Delta ABC}}\)
\( \Rightarrow {S_{\Delta GCF}} = \frac{1}{6}{S_{\Delta ABC}} = \frac{1}{6}.\frac{1}{2}.30.30 = 75\left( {c{m^2}} \right)\)
Chọn C
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 9 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Tam giác ABC có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
A. 2S
B. 3S
C. 4S
D. 6S
Phương pháp giải
Xác định \({S_{ABC}}\) trước khi tăng, sau khi tăng \(B’C = 2BC,CA’ = 3CA\) => \({S_{A’B’C}} = \frac{1}{2}B’C.A’C\sin C \)
Lời giải chi tiết
Trước khi tăng ta có diện tích tam giác \({S_{ABC}} = \frac{1}{2}BC.CA.\sin C\)
Sau khi tăng ta có: \(B’C = 2BC,CA’ = 3CA\), suy ra diện tích tam giác sau khi tăng là
\({S_{A’B’C}} = \frac{1}{2}B’C.A’C\sin C = \frac{1}{2}.2BC.3CA.\sin C = 6{S_{ABC}}\)
Chọn D
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 10 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Cho \(\widehat {xOy} = 30^\circ \). Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho \(AB = 1\). Độ dài lớn nhất của đoạn OB bằng:
A. 1,5
B. \(\sqrt 3 \)
C. \(2\sqrt 2 \)
D. 2
Phương pháp giải
Áp dụng định lí sin trong tam giác OAB để tính OB.
Lời giải chi tiết
Ta có: \(\frac{{AB}}{{\sin O}} = \frac{{OB}}{{\sin A}} \Rightarrow OB = \sin A.\frac{1}{{\sin {{30}^ \circ }}} = 2\sin A \le 2\)
Dấu bằng xảy ra khi \(\sin A = 1\) hay \(AB \bot Oy\)
Chọn D.
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 1 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Cho tam giác ABC với ba cạnh a, b, c. Chứng minh rằng:
\(\frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c} = \frac{{{a^2} + {b^2} + {c^2}}}{{2abc}}\)
Phương pháp giải
Áp dụng định lí côsin:
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} – 2bc\cos A\\{b^2} = {c^2} + {a^2} – 2ca\cos B\\{c^2} = {a^2} + {b^2} – 2ab\cos C\end{array}\)
Lời giải chi tiết
Từ định lí côsin ta suy ra
\(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} – {c^2}}}{{2ab}}\)
Suy ra:
\(\begin{array}{l}\frac{{\frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}}}{a} + \frac{{\frac{{{a^2} + {c^2} – {b^2}}}{{2ac}}}}{b} + \frac{{\frac{{{a^2} + {b^2} – {c^2}}}{{2ab}}}}{c}\\ = \frac{{\left( {{b^2} + {c^2} – {a^2}} \right) + \left( {{a^2} + {c^2} – {b^2}} \right) + \left( {{a^2} + {b^2} – c} \right)}}{{2abc}}\\ = \frac{{{a^2} + {b^2} + {c^2}}}{{2abc}}\end{array}\)
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 2 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Cho tam giác ABC. Biết \(a = 24,b = 36,\widehat C = 52^\circ \). Tính cạnh c và hai góc \(\widehat A,\widehat B\)
Phương pháp giải
Áp dụng định lí côsin, định lí sin
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
+ \(\begin{array}{l}{a^2} = {b^2} + {c^2} – 2bc\cos A\\{b^2} = {c^2} + {a^2} – 2ca\cos B\\{c^2} = {a^2} + {b^2} – 2ab\cos C\end{array}\)
+ \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\)
Lời giải chi tiết
Áp dụng định lí côsin ta có:
\(\begin{array}{l}{c^2} = {a^2} + {b^2} – 2ab\cos C = {24^2} + {36^2} – 2.24.36.\cos 52^\circ \simeq 808,137\\ \Rightarrow c \simeq 28,43\end{array}\)
Áp dụng định lí sin ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = \frac{{28,43}}{{\sin 52^\circ }}\)
Ta tính được
\(\begin{array}{l}\sin A \simeq 0,666 \Rightarrow \widehat A \simeq 41^\circ 42’\\\sin B \simeq 0,999 \Rightarrow \widehat B \simeq 86^\circ 18’\end{array}\)
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 3 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Hai chiếc tàu thủy P và Q cách nhau 50 m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển, người ta nhìn chiều cao AB của tháp dưới các góc \(\widehat {BPA} = 40^\circ \) và \(\widehat {BQA} = 52^\circ \). Tính chiều cao của tháp hải đăng đó.
Phương pháp giải
Áp dụng định lí sin
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\)
Lời giải chi tiết
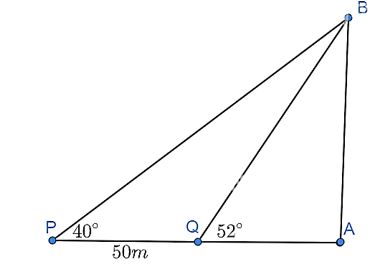
Góc \(\widehat {PQB}\) là góc bù của tam giác BPQ nên ta có:
\(\widehat {BQP} = \widehat {QPB} + \widehat {PBQ} \Rightarrow \widehat {PBQ} = \widehat {BQP} – \widehat {QPB} = 52^\circ – 40^\circ = 12^\circ \)
Áp dụng định lí sin trong tam giác BPQ ta có
\(\frac{{PQ}}{{\sin B}} = \frac{{BQ}}{{\sin P}} = \frac{{50}}{{\sin 12^\circ }} \Rightarrow BQ = \frac{{50}}{{\sin 12^\circ }}.\sin P = \frac{{50}}{{\sin 12^\circ }}.\sin 40^\circ \)
Áp dụng định lí sin vào tam giác ABQ ta có:
\(\frac{{BQ}}{{\sin A}} = \frac{{AB}}{{\sin Q}} \Rightarrow AB = \frac{{BQ}}{{\sin A}}.\sin Q = \frac{{\frac{{50}}{{\sin 12^\circ }}.\sin 40^\circ }}{{\sin 90^\circ }}.\sin 52^\circ \simeq 121,81\) (m)
Vậy chiều cao của tháp hải đăng là khoảng 121,81 m
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 4 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Cho \(\Delta ABC\) có \(\widehat A = 99^\circ ,b = 6,c = 10\). Tính:
a) Diện tích tam giác ABC
b) Bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp tam giác ABC
Phương pháp giải
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
+ \(\begin{array}{l}{a^2} = {b^2} + {c^2} – 2bc\cos A\\{b^2} = {c^2} + {a^2} – 2ca\cos B\\{c^2} = {a^2} + {b^2} – 2ab\cos C\end{array}\)
+ \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\)
Lời giải chi tiết
a) Áp dụng định lí sin vào tam giác ABC ta có:
\({S_{ABC}} = \frac{1}{2}bc\sin A = \frac{1}{2}.6.10.\sin 99^\circ \simeq 29,63\) (đvdt)
b) Áp dụng định lí côsin ta tính được:
\(a = \sqrt {{b^2} + {c^2} – 2bc\cos A} = \sqrt {{6^2} + {{10}^2} – 2.6.10\cos 99^\circ } \simeq 12,44\)
Bán kính đường tròn ngoại tiếp tam giác ABC là:
\(R = \frac{{abc}}{{4S}} \simeq \frac{{12,44.6.10}}{{4.29,63}} \simeq 6,25\)
Bán kính đường tròn nội tiếp tam giác là:
\(r = \frac{S}{p} = \frac{{29,63}}{{\frac{{\left( {12,44 + 6 + 10} \right)}}{2}}} \simeq 2,084\)
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 5 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Hai máy bay rời một sân bay cùng một lúc. Một chiếc máy bay với vận tốc 800 km/h theo hướng lệch so với hướng bắc \(15^\circ \) về hướng tây. Chiếc còn lại bay theo hướng lệch so với hướng nam \(45^\circ \) về phía tây với vận tốc 600 km/h (hình 1). Hỏi hai máy bay đó cách nhau bao xa sau 3 giờ?
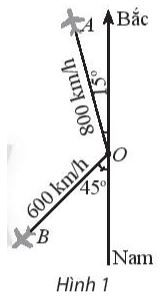
Phương pháp giải
Áp dụng định lí côsin:
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} – 2bc\cos A\\{b^2} = {c^2} + {a^2} – 2ca\cos B\\{c^2} = {a^2} + {b^2} – 2ab\cos C\end{array}\)
Lời giải chi tiết
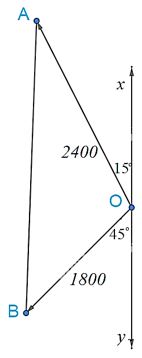
Sau 3 giờ khoảng cách máy bay so với sân bay là: \(OA = 2400\)km, \(OB = 1800\) km
Ta có
\(\widehat {xOA} + \widehat {AOB} + \widehat {BOy} = 180^\circ \Rightarrow \widehat {AOB} = 180^\circ – \left( {\widehat {xOA} + \widehat {BOy}} \right) = 180^\circ – \left( {15^\circ + 45^\circ } \right) = 120^\circ \)
Áp dụng định lí côsin ta có:
\(\begin{array}{l}AB = \sqrt {O{A^2} + O{B^2} – 2OA.OB.\cos \widehat {AOB}} \\ = \sqrt {{{2400}^2} + {{1800}^2} – 2.2400.1800.\cos 120^\circ } \simeq 3649,66\end{array}\)
Vậy khoảng cách của hai máy bay sau 3 giờ là khoảng 3649,66 km
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 6 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Cho tam giác ABC không vuông. Chứng minh rằng: \(\frac{{\tan A}}{{\tan B}} = \frac{{{c^2} + {a^2} – {b^2}}}{{{c^2} + {b^2} – {a^2}}}\)
Phương pháp giải
Áp dụng định lí côsin, định lí sin
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
+ \(\begin{array}{l}{a^2} = {b^2} + {c^2} – 2bc\cos A\\{b^2} = {c^2} + {a^2} – 2ca\cos B\\{c^2} = {a^2} + {b^2} – 2ab\cos C\end{array}\)
+ \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\)
Lời giải chi tiết
Tam giác ABC không vuông nên \(\tan A,\tan B,\tan C\) xác định
Áp dụng định lý sin và định lí cosin, ta có:
\(\begin{array}{l}
\tan A = \frac{{\sin A}}{{\cos A}} = \frac{a}{{2R}}:\frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{{abc}}{{4R.\left( {{b^2} + {c^2} – {a^2}} \right)}}\\
\tan B = \frac{{\sin B}}{{\cos B}} = \frac{b}{{2R}}:\frac{{{a^2} + {c^2} – {b^2}}}{{2ac}} = \frac{{abc}}{{4R.\left( {{c^2} + {a^2} – {b^2}} \right)}}
\end{array}\)
\( \Rightarrow \frac{{\tan A}}{{\tan B}} = \frac{{abc}}{{4R.\left( {{b^2} + {c^2} – {a^2}} \right)}}:\frac{{abc}}{{4R.\left( {{a^2} + {c^2} – {b^2}} \right)}} = \frac{{{c^2} + {a^2} – {b^2}}}{{{c^2} + {b^2} – {a^2}}}\) (dpcm)
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
Giải bài 7 trang 81 SBT Toán 10 Chân trời sáng tạo tập 1 – CTST
Một tháp viễn thông cao 42m được dựng thẳng đứng trên một sườn dốc \(34^\circ \)so với phương ngang. Từ đỉnh tháp người ta neo một sợi dây cáp xuống một điểm trên sườn dốc cách chân tháp 33 m như hình 2. Tính chiều dài của sợi dây đó.
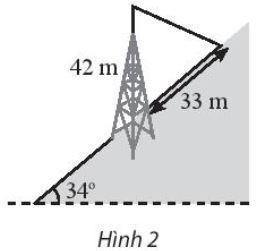
Phương pháp giải
Áp dụng định lí côsin:
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} – 2bc\cos A\\{b^2} = {c^2} + {a^2} – 2ca\cos B\\{c^2} = {a^2} + {b^2} – 2ab\cos C\end{array}\)
Lời giải chi tiết
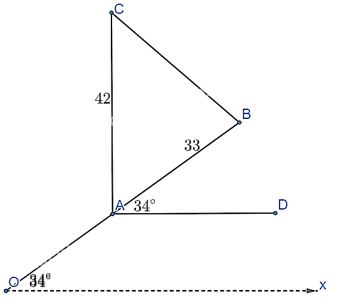
Ta có Ox song song với AD nên \(\widehat {AOx} = \widehat {BAD}\) (so le trong)
Mặt khác ta có : \(\widehat {CAB} + \widehat {BAD} = 90^\circ \Rightarrow \widehat {CAB} = 90^\circ – \widehat {BAD} = 56^\circ \)
Áp dụng đinhh lí côsin ta có :
\(BC = \sqrt {A{B^2} + A{C^2} – 2.AB.AC.\cos \widehat {BAC}} = \sqrt {{{33}^2} + {{42}^2} – 2.33.42.\cos 56^\circ } \simeq 36,1\)m
Vậy chiều dài sợi dây đó gần bằng 36,1 m
GIẢI SBT Toán 10 Chân trời sáng tạo Bài tập cuối chương 4
===========
THUỘC: Giải sách bài tập Toán 10 – Chân trời
