Giải SBT Bài 2. Tập hợp và các phép toán trên tập hợp – Toán 10 KNTT
Giải bài 1.9
Đề bài
Điền Đ vào ô trống nếu mệnh đề đúng, điền S vào ô trống nếu mệnh đề sai.
Phương pháp giải – Xem chi tiết
+Tập hợp rỗng: \(\emptyset\), là tập không có phần tử nào.
+ \(A \subset B \Leftrightarrow \forall x \in A:x \in B\)
đặc biệt: \(\emptyset \subset A,\forall A.\)
Lời giải chi tiết
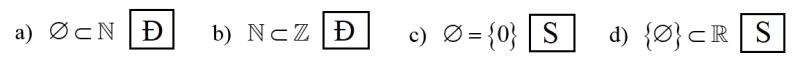
c) Sai vì \(\emptyset\) là tập không có phần tử nào, còn \(\{0\}\) là tập có một phần tử là 0.
d) Sai vì kì hiệu \(\emptyset\) là tập hợp, không phải phần tử nên viết \(\{\emptyset\}\) là sai.
Giải bài 1.10
Đề bài
Cho hai tập hợp \(A,\,\,B\) được mô tả bởi biểu đồ ven như sau:
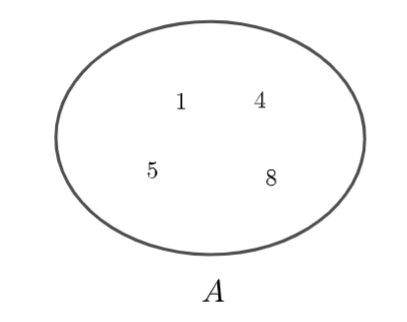
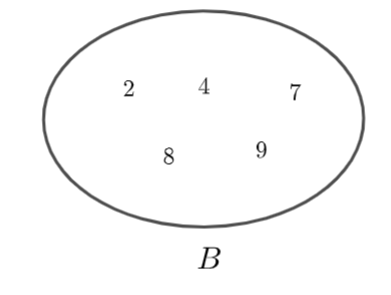
a) Hãy chỉ ra các phần tử của tập hợp \(A,\) tập hợp \(B.\)
b) Tính \(n\left( {A \cup B} \right)\)
c) Hãy chỉ ra các phần tử thuộc tập hợp \(A\) mà không thuộc tập hợp \(B.\)
d) Hãy chỉ ra các phần tử thuộc tập hợp \(B\) mà không thuộc tập hợp \(A.\)
Phương pháp giải – Xem chi tiết
– Viết các phần tử cửa tập hợp A, tập hợp B dưới dạng liệt kê
– \(A \cup B\) là tập hợp các phần tử hoặc thuộc tập hợp A hoặc thuộc tập hợp B
– Viết các phần tử của tập hợp A những không thuộc tập hợp B và ngược lại
Lời giải chi tiết
a) \(A = \left\{ {1;4;5;8} \right\},\quad B = \left\{ {2;4;7;8;9} \right\}\)
b) \(A \cup B = \left\{ {1;2;4;5;7;8;9} \right\}\,\, \Rightarrow \,\,n\left( {A \cup B} \right) = 7.\)
c) \(A\backslash B = \left\{ {1;5} \right\}\)
d) \(B\backslash A = \left\{ {2;7;9} \right\}\)
Giải bài 1.11
Đề bài
Xác định các tập hợp sau bằng cách nêu tính chất đặc trưng cho các phần tử của tập hợp.
\(A = \left\{ {0;4;8;12;16} \right\},\quad B = \left\{ { – 3;9; – 37;81} \right\}\)
\(C\) là đường thẳng trung trực của đoạn thẳng \(AB.\)
Phương pháp giải – Xem chi tiết
– các phần tử của tập hợp A là các số tự nhiên chia hết cho 4, \(0 < x \le 16.\)
– các phần tử của tập hợp B là các lũy thừa với cơ số \( – 3\) và số mũ tăng dần từ \(1 \le x \le 4.\)
– các điểm nằm trên đường trung trực của đoạn thẳng \(AB\) thì cách đều hai đầu mút \(A\) và \(B.\)
Lời giải chi tiết
Tính đặc trưng cho các phần tử của tập hợp trên là:
\(\begin{array}{l}A = \left\{ {\left. {4x} \right|x \in \mathbb{N};\,\,x \le 4} \right\}.\\B = \left\{ {\left. {{{\left( { – 3} \right)}^x}} \right|x \in \mathbb{N};\,\,1 \le x \le 4} \right\}.\\C = \left\{ {\left. P \right|PA = PB} \right\}.\end{array}\)
Giải bài 1.12
Đề bài
Trong các tập hợp sau, tập hợp nào rỗng?
\(A = \left\{ {\left. {x \in \mathbb{N}} \right|x \le 0} \right\};\quad B = \left\{ {\left. {x \in \mathbb{N}} \right|2{x^2} – 3x – 5 = 0} \right\}\)
Phương pháp giải – Xem chi tiết
Liệt kê các phần tử của A, B.
Tập hợp rỗng là tập không có phần tử nào.
Lời giải chi tiết
\(A = \left\{ 0 \right\}\) nên tập hợp A không phải là tập rỗng.
Giải phương trình: \(2{x^2} – 3x – 5 = 0\,\, \Leftrightarrow \left( {x + 1} \right)\left( {2x – 5} \right) = 0\,\, \\\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = – 1 \,(KTM)}\\{x = \frac{5}{2}\,(KTM)}\end{array}} \right.\)
Vậy \(B = \emptyset \) hay B là tập hợp rỗng.
Giải bài 1.13
Đề bài
Trong các mệnh đề sau, mệnh đề nào đúng? Mệnh đề nào sai? Giải thích kết luận đưa ra.
a) Tập rỗng là tập con của mọi tập hợp
b) Nếu \(X = \left\{ {a;b} \right\}\) thì \(a \subset X\)
c) Nếu \(X = \left\{ {a;b} \right\}\) thì \(\left\{ {a;b} \right\} \subset X\)
Lời giải chi tiết
a) Mệnh đề: “Tập rỗng là tập con của mọi phần tử” là mệnh đề đúng.
b) Mệnh đề: “Nếu \(X = \left\{ {a;b} \right\}\) thì \(a \subset X\)” là mệnh đề sai.
Vì nếu \(X = \left\{ {a;b} \right\}\) thì \(a \in X\)
c) Mệnh đề: “Nếu \(X = \left\{ {a;b} \right\}\) thì \(\left\{ {a;b} \right\} \subset X\)” là mệnh đề đúng.
Mọi tập hợp là tập con của chính tập hợp đó.
Giải bài 1.14
Đề bài
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
| a) \(\left( {4;7} \right) \cap \left( { – 1;3} \right)\) | b) \(\left( { – 2;1} \right] \cap \left( { – \infty ;1} \right)\) |
| c) \(( – 2; 6) \) \ \((3;10)\) | d) \((- 3;5)\) \ \([2;8)\) |
Lời giải chi tiết
a) \(\left( {4;7} \right) \cap \left( { – 1;3} \right) = \emptyset \)
b) \(\left( { – 2;1} \right] \cap \left( { – \infty ;1} \right) = \left( { – 2;1} \right)\)

c) \((- 2;6)\) \ \((3;10) = \left( { – 2;3} \right]\)

d) \((- 3;5)\) \ \([2;8)\) \(= \left( { – 3;2} \right)\)

Giải bài 1.15
Đề bài
Trong một cuộc phỏng vấn 56 người về những việc họ thường làm vào ngày nghỉ cuối tuần, có 24 người thích tập thể thao, 15 người thích đi câu cá và 20 người không thích cả hai hoạt động trên.
a) Có bao nhiêu người thích chơi thể thao hoặc thích câu cá?
b) Có bao nhiêu người thích cả câu cá và chơi thể thao?
c) Có bao nhiêu người chỉ thích câu cá, không thích chơi thể thao?
Phương pháp giải – Xem chi tiết
– Vẽ sơ đồ ven để biểu diễn những việc họ thường làm vào ngày cuối tuần
– Tính số người thích chơi thể thao hoặc thích câu cá
– Tính số người thích chơi câu cá và chơi thể thao
– Tính số người thích chơi câu cá nhưng không thích thể thao
Lời giải chi tiết
Gọi A là số người thích chơi thể thao, B là số người thích câu cá, \(A \cap B\) là số người thích cả câu cá và chơi thể thao. Ta có sơ đồ ven:
a) Số người thích chơi thể thao hoặc thích câu cá là: \(56 – 20 = 36\) (người).
b) Số người thích cả câu cá và thể thao là: \(24 + 15 – 36 = 3\) (người).
c) Số người thích chơi câu cá nhưng không thích thể thao là: \(15 – 3 = 12\) (người).
