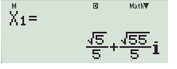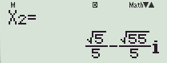Giải bài tập Toán 9 Bài 2 (Chân trời sáng tạo): Phương trình bậc hai một ẩn

Giải chi tiết Giải bài tập Toán 9 Bài 2 (Chân trời sáng tạo): Phương trình bậc hai một ẩn – SÁCH GIÁO KHOA TOÁN 9 CHÂN TRỜI SÁNG TẠO – 2024

================

Giải bài tập Toán 9 Bài 2: Phương trình bậc hai một ẩn

Khởi động trang 11 Toán 9 Tập 2:Sau khi ném theo chiều từ dưới lên, độ cao h (m) của một quả bóng theo thời gian t (giây) được xác định bởi công thức h = 2 + 9 t – 5t². Thời gian từ lúc ném cho đến khi bóng chạm đất là bao lâu?

Lời giải:

Sau bài học này ta giải quyết được bài toán như sau:

Khi bóng chạm đất thì chiều cao h = 0 nên ta có phương trình: 2 + 9t – 5t²= 0

Giải phương trình 2 + 9t – 5t²= 0 (t > 0) ta có: a = –5; b = 9; c = 2.

Δ = 9²– 4 . (−5) . 2 = 121 > 0.

Vậy phương trình có hai nghiệm phân biệt là:

$t_1=\frac{-9+\sqrt{121}}{2\cdot \left(-5\right)}=\frac{-1}{5}$(loại);$t_2=\frac{-9-\sqrt{121}}{2\cdot \left(-5\right)}=2$(thỏa mãn).

Vậy thời gian từ lúc ném cho đến khi bóng chạm đất là 2 giây.

1. Phương trình bậc hai một ẩn

Khám phá 1 trang 11 Toán 9 Tập 2:Một tấm thảm hình chữ nhật có chiều dài hơn chiều rộng 2 m. Biết diện tích tấm thảm bằng 24 m². Gọi x (m) là chiều rộng tấm thảm (x > 0). Hãy viết phương trình với ẩn x biểu thị mối quan hệ giữa chiều, chiều rộng và diện tích của tấm thảm.

Lời giải:

Gọi x (m) là chiều rộng tấm thảm (x > 0) suy ra chiều dài là x + 2 (m).

Biết diện tích tấm thảm bằng 24 m²nên ta có phương trình:

x.(x + 2) = 24 hay x²+ 2x = 24.

Vậy phương trình với ẩn x biểu thị mối quan hệ giữa chiều, chiều rộng và diện tích của tấm thảm là x²+ 2x = 24.

Thực hành 1 trang 11 Toán 9 Tập 2:Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn? Chỉ rõ các hệ số a, b, c của mỗi phương trình bậc hai một ẩn đó.

a) −7x²= 0;

b)$-12x^2+7x-\sqrt{3}=0;$

c) x³+ 5x – 6 = 0;

d) x²– (m + 2)x + 7 = 0 (m là số đã cho).

Lời giải:

a) Phương trình −7x²= 0 là phương trình bậc hai một ẩn với a = −7; b = 0; c = 0.

b) Phương trình$-12x^2+7x-\sqrt{3}=0$là phương trình bậc hai một ẩn với a = −12; b = 7;$c=-\sqrt{3}$.

c) Phương trình x³+ 5x – 6 = 0 không là phương trình bậc hai một ẩn vì số hạng x³có chứa bậc 3.

d) Phương trình x²– (m + 2)x + 7 = 0 là phương trình bậc hai một ẩn với a = 1;

b = –(m + 2) ; c = 7.

2. Giải phương trình bậc hai dạng đặc biệt

Khám phá 2 trang 12 Toán 9 Tập 2:a) Bằng cách đưa về phương trình tích, hãy giải các phương trình sau:

i) 3x²– 12x = 0;

ii) x²– 16 = 0.

b) Để đưa các phương trình bậc hai dạng đặc biệt trên về phương trình tích ta đã dùng các phép biến đổi nào?

Lời giải:

a) i) 3x²– 12x = 0

3x(x – 4) = 0

x = 0 hoặc x – 4 = 0

x = 0 hoặc x = 4.

Vậy phương trình 3x²– 12x = 0 có hai nghiệm x = 0 và x = 4.

ii) x²– 16 = 0

(x – 4)(x + 4) = 0

x – 4 = 0 hoặc x + 4 = 0

x = 4 hoặc x = –4.

Vậy phương trình x²– 16 = 0 có hai nghiệm x = –4 và x = 4.

b) Để đưa các phương trình bậc hai dạng đặc biệt trên về phương trình tích ta đã dùng phương pháp đặt nhân tử chung và hằng đẳng thức.

Thực hành 2 trang 12 Toán 9 Tập 2:Giải các phương trình:

a) 3x²– 27 = 0;

b) x²– 10x + 25 = 16.

Lời giải:

a) 3x²– 27 = 0

3x²= 27

x²= 9

x = 3 hoặc x = –3.

Vậy phương trình có hai nghiệm x = 3 và x = –3.

b) x²– 10x + 25 = 16

(x – 5)²= 16

(x – 5)²= 4²

x – 5 = 4 hoặc x – 5 = –4

x = 9 hoặc x = 1.

Vậy phương trình có hai nghiệm x = 9 và x = 1.

3. Công thức nghiệm của phương trình bậc hai

Khám phá 3 trang 13 Toán 9 Tập 2:Cho phương trình bậc hai x²– 4x + 3 = 0.

a) Thay mỗi dấubằng số thích hợp để viết lại phương trình đã cho thành:

b) Giải phương trình (*), từ đó tìm nghiệm phương trình đã cho.

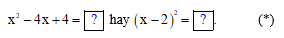
Lời giải:

a) Ta có x²– 4x + 3 = 0

x²– 4x + 4 = 1

x²– 2 . 2x + 2²= 1

(x – 2)²= 1.

Vậy ta điền như sau:$x^2–4x+4=1$hay${\left(x-2\right)}^2=1.$

b) Giải phương trình (*), ta được:

(x – 2)²= 1

x – 2 = 1 hoặc x – 2 = –1

x = 3 hoặc x = 1.

Vậy phương trình (*) có hai nghiệm x = 3 và x = 1.

Thực hành 3 trang 14 Toán 9 Tập 2:Giải các phương trình:

a) 7x²– 3x + 2 = 0;

b)$3x^2–2\sqrt{3}x+1=0;$

c) –2x²+ 5x + 2 = 0.

Lời giải:

a) 7x²– 3x + 2 = 0

Ta có a = 7; b = –3; c = 2 nên ∆ = (–3)²– 4 . 7 . 2 = –47 < 0.

Vậy phương trình vô nghiệm.

b)$3x^2–2\sqrt{3}x+1=0$

Ta có$a=3;b=–2\sqrt{3};c=25$nên$\Delta ={\left(–2\sqrt{3}\right)}^2–4\cdot 3\cdot 1=0.$

Vậy phương trình có nghiệm kép$x_1=x_2=\frac{\sqrt{3}}{3}.$

c) –2x²+ 5x + 2 = 0.

Ta có a = –2; b = 5; c = 2 nên ∆ = 5²– 4 . (–2) . 2 = 41 > 0.

Vậy phương trình có hai nghiệm phân biệt là:

$x_1=\frac{-5+\sqrt{41}}{-4}=\frac{5-\sqrt{41}}{4};x_2=\frac{-5-\sqrt{41}}{-4}=\frac{5+\sqrt{41}}{4}.$

Thực hành 4 trang 14 Toán 9 Tập 2:Dùng công thức nghiệm thu gọn để giải các phương trình sau:

a) 5x²– 12x + 4 = 0;

b)$5x^2–2\sqrt{5}x+1=0.$

Lời giải:

a) 5x²– 12x + 4 = 0

Ta có a = 5; b’= –6; c = 4 nên ∆’= (–6)²– 5 . 4 = 16 > 0.

Vậy phương trình có hai nghiệm phân biệt là:$x_1=\frac{6+\sqrt{16}}{5}=2;x_2=\frac{6-\sqrt{16}}{5}=\frac{2}{5}.$

b)$5x^2–2\sqrt{5}x+1=0$

Ta có$a=5;b^{‘}=–\sqrt{5};c=1$nên${\Delta }^{‘}={\left(–\sqrt{5}\right)}^2–5\cdot 1=0.$

Vậy phương trình có nghiệm kép$x_1=x_2=\frac{\sqrt{5}}{5}.$

Vận dụng trang 14 Toán 9 Tập 2:Trả lời câu hỏi trong Hoạt động khởi động (trang 11).

Lời giải:

Khi bóng chạm đất thì chiều cao h = 0 nên ta có phương trình: 2 + 9t – 5t²= 0

Giải phương trình 2 + 9t – 5t²= 0 (t > 0) ta có: a = –5; b = 9; c = 2.

Δ = 9²– 4 . (−5) . 2 = 121 > 0.

Vậy phương trình có hai nghiệm phân biệt là:

$t_1=\frac{-9+\sqrt{121}}{2\cdot \left(-5\right)}=\frac{-1}{5}$(loại);$t_2=\frac{-9-\sqrt{121}}{2\cdot \left(-5\right)}=2$(thỏa mãn).

Vậy thời gian từ lúc ném cho đến khi bóng chạm đất là 2 giây.

4. Tìm nghiệm phương trình bậc hai một ẩn băng máy tính cầm tay

Thực hành 5 trang 16 Toán 9 Tập 2:Tìm các nghiệm của mỗi phương trình sau bằng máy tính cầm tay.

a) 3x²– 8x + 4 = 0;

b)$5x^2–2\sqrt{5}x+12=0;$

c) 2x²– 8x + 8 = 0

Lời giải:

− Ấn nútONđể khởi động máy.

− Ấn nútMODE, màn hình máy sẽ hiện ra các dòng như hình:

− Ấn nút3.

a) 3x²– 8x + 4 = 0

− Nhập các hệ số như sau:

Màn hình xuất hiện như hình bên:
− Ấn nút, kết quả xuất hiện như hình bên:

Vậy phương trình đã cho có nghiệm là x = 2 và$x=\frac{2}{3}.$

b)$5x^2–2\sqrt{5}x+12=0$

− Nhập các hệ số như sau:

Màn hình xuất hiện như hình bên:
− Ấn nút, kết quả xuất hiện như hình bên:

Vậy phương trình đã cho vô nghiệm.

c) 2x²– 8x + 8 = 0

− Nhập các hệ số như sau:

Màn hình xuất hiện như hình bên:

Vậy phương trình đã cho có nghiệm kép x = 2.

5. Giải bài toán bằng cách lập phương trình bậc hai

Khám phá 4 trang 16 Toán 9 Tập 2:Một mảnh đất hình chữ nhật có chu vi 100 m, diện tích 576 m². Gọi x (m) là chiều rộng của mảnh đất (0 < x < 50). Hãy lập phương trình biểu thị mối liên hệ giữa chiều rộng, chiều dài và diện tích của mảnh đất.

Lời giải:

Gọi x (m) là chiều rộng của mảnh đất (0 < x < 50).

Ta có chu vi 100 m nên chiều dài của mảnh đất là: 50 – x (m).

Mặt khác, diện tích là 576 m²nên ta có phương trình biểu thị mối liên hệ giữa chiều rộng, chiều dài và diện tích của mảnh đất là:

x(50 – x) = 576 suy ra –x²+ 50x – 576 = 0.

Vậy phương trình biểu thị mối liên hệ giữa chiều rộng, chiều dài và diện tích của mảnh đất là –x²+ 50x – 576 = 0.

Thực hành 6 trang 17 Toán 9 Tập 2:Một sân khấu ngoài trời có dạng hình chữ nhật, chiều dài hơn chiều rộng 2 m, độ dài đường chéo là 10 m. Tính diện tích của sân khấu đó.

Lời giải:

Gọi x (m) là chiều rộng của sân khấu (0 < x < 10).

Suy ra, chiều dài của sân khấu là: x + 2 (m).

Ta có độ dài đường chéo hình chữ nhật là 10 m nên áp dụng định lí Pythagore trong tam giác vuông thuộc hình chữ nhật ta được:

x²+ (x + 2)²= 10²

x²+ x²+ 4x + 4 – 100 = 0

2x²+ 4x – 96 = 0

x²+ 2x – 48 = 0.

Giải phương trình trên, ta được:

x₁= 6 (thỏa mãn), x₂= −8 (loại).

Suy ra chiều rộng của sân khấu là 6 m, chiều dài là 8 m.

Vậy diện tích của sân khấu là S = 6 . 8 = 48 (m²).

Bài tập

Bài 1 trang 17 Toán 9 Tập 2:Giải các phương trình:

a) 5x²+ 7x = 0;

b) 5x²– 15 = 0.

Lời giải:

a) 5x²+ 7x = 0

x(5x + 7) = 0

x = 0 hoặc 5x + 7 = 0

x = 0 hoặc$x=\frac{-7}{5}$.

Vậy phương trình có hai nghiệm là x = 0 và$x=\frac{-7}{5}$.

b) 5x²– 15 = 0

5x²= 15

x²= 3

$x=\pm \sqrt{3}$

Vậy phương trình có hai nghiệm là$x=\pm \sqrt{3}$

Bài 2 trang 17 Toán 9 Tập 2:Dùng công thức nghiệm thu gọn để giải các phương trình sau:

a) x²– x – 20 = 0;

b) 6x²– 11x – 35 = 0;

c) 16y²+ 24y + 9 = 0;

d) 3x²+ 5x + 3 = 0;

e)$x^2–2\sqrt{3}x-6=0;$

g)$x^2–\left(2+\sqrt{3}\right)x+2\sqrt{3}=0.$

Lời giải:

a) x²– x – 20 = 0

Ta có a = 1; b = –1; c = –20 nên ∆ = (–1)²– 4 . 1 . (–20) = 81 > 0.

Vậy phương trình có hai nghiệm phân biệt là:$x_1=\frac{1+\sqrt{81}}{2}=5;x_2=\frac{1-\sqrt{81}}{2}=-4.$

b) 6x²– 11x – 35 = 0

Ta có a = 6; b = –11; c = –35 nên ∆ = (–11)²– 4 . 6 . (–11) = 961 > 0.

Vậy phương trình có hai nghiệm phân biệt là:$x_1=\frac{11+\sqrt{961}}{2\cdot 6}=\frac{7}{2};x_2=\frac{11-\sqrt{961}}{2\cdot 6}=-\frac{5}{3}.$

c) 16y²+ 24y + 9 = 0

Ta có a = 16; b’= 12; c = 9 nên ∆’= 12²– 16 . 9 = 0

Vậy phương trình có nghiệm kép$x_1=x_2=-\frac{12}{16}=-\frac{3}{4}.$

d) 3x²+ 5x + 3 = 0

Ta có a = 3; b = 5; c = 3 nên ∆ = 3²– 4 . 5 . 3 = –51 < 0.

Vậy phương trình vô nghiệm.

e)$x^2–2\sqrt{3}x-6=0$

Ta có$a=1;b^{‘}=–\sqrt{3};c=-6$nên${\Delta }^{‘}={\left(–\sqrt{3}\right)}^2-1\cdot \left(-6\right)=3+6=9$.

Vậy phương trình có hai nghiệm phân biệt là:$x_1=\frac{\sqrt{3}+\sqrt{9}}{1}=3+\sqrt{3};x_2=\frac{\sqrt{3}-\sqrt{9}}{1}=-3+\sqrt{3}.$

g)$x^2–\left(2+\sqrt{3}\right)x+2\sqrt{3}=0$

Ta có$a=1;b=–\left(2+\sqrt{3}\right);c=2\sqrt{3}$nên

$\Delta ={\left[–\left(2+\sqrt{3}\right)\right]}^2-4\cdot 1\cdot 2\sqrt{3}=7+4\sqrt{3}-8\sqrt{3}=7-4\sqrt{3}$

Vậy phương trình có hai nghiệm phân biệt là:

$x_1=\frac{2+\sqrt{3}+\sqrt{7-4}\sqrt{3}}{2}=2;x_2=\frac{2+\sqrt{3}-\sqrt{7-4}\sqrt{3}}{1}=\sqrt{3}.$

Bài 3 trang 17 Toán 9 Tập 2:Giải các phương trình:

a) x(x + 8) = 20;

b) x(3x – 4) = 2x²+ 5;

c) (x – 5)²+ 7x = 65;

d) (2x + 3)(2x – 3) = 5(2x + 3).

Lời giải:

a) x(x + 8) = 20

x²+ 8x – 20 = 0

Ta có a = 1; b’= 4; c = –20 nên ∆’= 4²– 1 . (–20) = 36 > 0.

Vậy phương trình có hai nghiệm phân biệt là:$x_1=\frac{-4+\sqrt{36}}{1}=2;x_2=\frac{-4-\sqrt{36}}{1}=-10.$

b) x(3x – 4) = 2x²+ 5

3x²– 4x = 2x²+ 5

x²– 4x – 5 = 0

Ta có a = 1; b’= –2; c = –5 nên ∆’= (–2)²– 1 . (–5) = 9 > 0.

Vậy phương trình có hai nghiệm phân biệt là:$x_1=\frac{2+\sqrt{9}}{1}=5;x_2=\frac{2-\sqrt{9}}{1}=-1.$

c) (x – 5)²+ 7x = 65

x²– 10x + 25 + 7x = 65

x²– 3x – 40 = 0

Ta có a = 1; b = –3; c = –40 nên ∆ = (–3)²– 4 . 1 . (–40) = 169 > 0.

Vậy phương trình có hai nghiệm phân biệt là:$x_1=\frac{3+\sqrt{169}}{2}=8;x_2=\frac{3-\sqrt{169}}{2}=-5.$

d) (2x + 3)(2x – 3) = 5(2x + 3)

4x²– 9 = 10x + 15

4x²– 10x – 24 = 0

2x²– 5x – 12 = 0

Ta có a = 2; b = –5; c = –12 nên ∆ = (–5)²– 4 . 2 . (–12) = 121 > 0.

Vậy phương trình có hai nghiệm phân biệt là:$x_1=\frac{5+\sqrt{121}}{4}=4;x_2=\frac{5-\sqrt{121}}{4}=\frac{-3}{2}.$

Bài 4 trang 17 Toán 9 Tập 2:Quãng đường từ thành phố A đến thành phố B dài 150 km. Hai ô tô khởi động cùng một lúc từ A đến B. Biết tốc độ ô tô thứ nhất lớn hơn tốc độ ô tô thứ hai là 10 km/h và ô tô thứ nhất đến B trước ô tô thứ hai là 30 phút. Tính tốc độ của mỗi xe.

Lời giải:

Gọi tốc độ ô tô thứ nhất là x (km/h) (x > 0)

Suy ra tốc độ ô tô thứ hai là x – 10 (km/h)

Thời gian ô tô thứ hai đi từ thành phố A đến thành phố B là:$\frac{150}{x-10}$(giờ).

Thời gian ô tô thứ nhất đi từ thành phố A đến thành phố B là:$\frac{150}{x}$(giờ).

Vì ô tô thứ nhất đến B trước ô tô thứ hai là 30 phút$=\frac{1}{2}$giờ nên ta có phương trình:

$\frac{150}{x-10}-\frac{150}{x}=\frac{1}{2}$

Biến đổi phương trình trên, ta được:

150 . 2 . x – 2 . 150(x – 10) = x(x – 10) hay x²− 10x − 3 000 = 0.

Giải phương trình trên, ta được: x₁= 60 (thỏa mãn), x₂= −50 (loại).

Vậy tốc độ của ô tô thứ nhất là 60 km/h, ô tô thứ hai là 50 km/h.

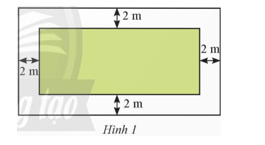
Bài 5 trang 17 Toán 9 Tập 2:Một khu vườn hình chữ nhật có chu vi 280 m. Người ta để một lối đi xung quanh vườn rộng 2 m. Phần đất còn lại dùng để trồng rau có diện tích 4 256 m²(Hình 1). Tính chiều dài và chiều rộng của khu vườn đó.

Lời giải:

Nửa chu vi của vườn là: 280 : 2 = 140 (m).

Gọi chiều dài của hình chữ nhật là x (m) (70 < x < 140).

Suy ra chiều rộng là 140 – x (m).

Mỗi bên để 2 m nên chiều dài của đất để lại trồng trọt chỉ còn x – 4 (m) và chiều rộng là 140 – x – 4 = 136 – x (m).

Theo bài ra, ta có phương trình: (x – 4)(136 – x) = 4256

Suy ra x²− 140x + 4 800 = 0

Giải phương trình trên ta có:

x₁= 60 (loại), x₂= 80 (thỏa mãn).

Vậy chiều dài của khu vườn là 80 m và chiều rộng là 60 m.

Bài 6 trang 17 Toán 9 Tập 2:Nếu đổ thêm 250 g nước vào một dung dịch chứa 50 g muối thì nồng độ dung dịch sẽ giảm 10

Lời giải:

Gọi khối lượng nước trong dung dịch trước khi đổ thêm nước là x (g) (x > 0).

Khối lượng dung dịch khi đó là x + 50 (g).

Nồng độ muối trong dung dịch khi đó là:$\frac{50}{x+50}$.

Nếu đổ thêm 250 g nước vào dung dịch thì khối lượng của dung dịch là:

x + 50 + 250 = x + 300 (g)

Nồng độ dung dịch lúc này là$\frac{50}{x+300}$.

Vì nồng độ dung dịch giảm 10