Giải Bài tập cuối chuyên đề 1 – Chuyên đề Toán 10 (Chân trời)

Giải Bài tập cuối chuyên đề 1 – Chuyên đề Toán 10 (Chân trời)
=========

Giải bài 1 trang 24 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Trong các hệ phương trình sau, hệ nào là hệ phương trình bậc nhất ba ẩn? Mỗi bộ ba số \(\left( { – 1;0;1} \right),\left( {\frac{1}{2}; – \frac{1}{2}; – 1} \right)\) có là nghiệm của các hệ phương trình bậc nhất ba ẩn đó không?

a) \(\left\{ \begin{array}{l}2x – y + z =  – 1\\ – x + 2y = 1\\3y – 2z =  – 2\end{array} \right.\)

b) \(\left\{ \begin{array}{l}4x – 2y + z = 2\\8x + 3z = 1\\ – 6y + 2z = 1\end{array} \right.\)

c) \(\left\{ \begin{array}{l}3x – 2y + zx = 2\\xy – y + 2z = 1\\x + 2y – 3yz =  – 2\end{array} \right.\)

Bộ ba số là nghiệm của hệ nếu nó thỏa mãn cả 3 phương trình của hệ.

Lời giải chi tiết

Hệ phương trình a), b) là hệ phương trình bậc nhất ba ẩn.

Hệ phương trình c) không phải là hệ phương trình bậc nhất vì chứa \(zx,xy,yz.\)

+) Bộ ba số (-1;0;1) là nghiệm của hệ phương trình a) vì

\(\left\{ \begin{array}{l}2.( – 1) – 0 + 1 =  – 1\\ – ( – 1) + 2.0 = 1\\3.0 – 2.1 =  – 2\end{array} \right.\) (nghiệm đúng cả ba phương trình của hệ).

 

+) Bộ ba số (-1;0;1) không là nghiệm của hệ phương trình b) vì \(4.( – 1) – 2.0 + 1 =  – 3 \ne 2\) (không là nghiệm của phương trình \(4x – 2y + z\))

+) Bộ ba số \(\left( {\frac{1}{2}; – \frac{1}{2}; – 1} \right)\) không là nghiệm của hệ phương trình a) vì \( – \frac{1}{2} + 2.\left( { – \frac{1}{2}} \right) =  – \frac{3}{2} \ne 1\) (không là nghiệm của phương trình \( – x + 2y = 1\))

+) Bộ ba số \(\left( {\frac{1}{2}; – \frac{1}{2}; – 1} \right)\) là nghiệm của hệ phương trình b) vì

\(\left\{ \begin{array}{l}4.\frac{1}{2} – 2.\left( { – \frac{1}{2}} \right) + ( – 1) = 2\\8.\frac{1}{2} + 3.( – 1) = 1\\ – 6.\left( { – \frac{1}{2}} \right) + 2.( – 1) = 1\end{array} \right.\) (nghiệm đúng cả ba phương trình của hệ).

Giải bài 2 trang 24 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Giải các hệ phương trình sau bằng phương pháp Gauss:

a) \(\left\{ \begin{array}{l}x – 2y + z = 3\\ – y + z = 2\\y + 2z = 1\end{array} \right.\)

b) \(\left\{ \begin{array}{l}3x – 2y – 4z = 3\\4x + 6y – z = 17\\x + 2y = 5\end{array} \right.\)

c) \(\left\{ \begin{array}{l}x + y + z = 1\\3x – y – z = 4\\x + 5y + 5z =  – 1\end{array} \right.\)

Lời giải chi tiết

a) \(\left\{ \begin{array}{l}x – 2y + z = 3\quad (1)\\ – y + z = 2\quad \quad (2)\\y + 2z = 1\quad \quad (3)\end{array} \right.\)

Cộng vế với vế của phương trình (2) với phương trình (3), giữ nguyên phương trình (1) và (2) ta được hệ:

\(\left\{ \begin{array}{l}x – 2y + z = 3\quad (1)\\ – y + z = 2\quad \quad (2)\\3z = 3\quad \quad \quad (3.1)\end{array} \right.\)

Từ phương trình (3.1) ta có \(z = 1\)

Thay \(z = 1\) vào phương trình (2) ta được \(y =  – 1\)

Thay \(y =  – 1\) và \(z = 1\) vào phương trình (1) ta được \(x = 0\)

Vậy hệ phương trình đã cho có nghiệm duy nhất là \(\left( {0; – 1;1} \right)\)

b) \(\left\{ \begin{array}{l}3x – 2y – 4z = 3\quad (1)\\4x + 6y – z = 17\quad (2)\\x + 2y = 5\quad \quad \quad \;\;(3)\end{array} \right.\)

Cộng vế với vế của phương trình (1) với phương trình (3), giữ nguyên phương trình (2) và (3) ta được hệ:

\(\left\{ \begin{array}{l}4x – 4z = 8\quad \quad \quad (1.1)\\4x + 6y – z = 17\quad (2)\\x + 2y = 5\quad \quad \quad \;\;(3)\end{array} \right.\)

Nhân hai vế của phương trình (1.1) với -1, cộng vế với vế của phương trình nhận được với phương trình (2), giữ nguyên phương trình (1) và (3) ta được hệ:

\(\left\{ \begin{array}{l}4x – 4z = 8\quad \quad (1.1)\\6y + 3z = 9\quad \quad (2)\\x + 2y = 5\quad \;\;(3)\end{array} \right.\) hay \(\left\{ \begin{array}{l}x – z = 2\quad \quad (1.1)\\2y + z = 3\quad \quad (2)\\x + 2y = 5\quad \;\;(3)\end{array} \right.\)

Cộng vế với vế của phương trình (1) với phương trình (2), giữ nguyên phương trình (1) và (3) ta được hệ:

\(\left\{ \begin{array}{l}x – z = 2\quad \quad (1.1)\\x + 2y = 5\quad \;\;(2.1)\\x + 2y = 5\quad \;\;(3)\end{array} \right.\)

Hai phương trình (2.1) và (3) giống nhau, nên có thể viết hệ phương trình thành:

\(\left\{ \begin{array}{l}x – z = 2\quad \quad (1.1)\\x + 2y = 5\quad \;\;(2.1)\end{array} \right.\)

Từ phương trình (1.1), ta có \(x = z + 2\), thay vào phương trình (2.1) ta được \(z =  – 2y + 3\), từ đó suy ra \(x =  – 2y + 5\)

Vậy hệ phương trình đã cho có vô số nghiệm dạng \(( – 2y + 5;y; – 2y + 3)\) với \(y \in \mathbb{R}\).

 

c) \(\left\{ \begin{array}{l}x + y + z = 1\quad (1)\\3x – y – z = 4\quad (2)\\x + 5y + 5z =  – 1\quad (3)\end{array} \right.\)

Nhân hai vế của phương trình (1) với -3, cộng vế với vế của phương trình nhận được với phương trình (2), giữ nguyên phương trình (1) và (3) ta được hệ:

\(\left\{ \begin{array}{l}x + y + z = 1\quad (1)\\ – 4y – 4z = 1\quad (2.1)\\x + 5y + 5z =  – 1\quad (3)\end{array} \right.\)

Nhân hai vế của phương trình (1) với -1, cộng vế với vế của phương trình nhận được với phương trình (3), giữ nguyên phương trình (1) và (2.1) ta được hệ:

\(\left\{ \begin{array}{l}x + y + z = 1\quad (1)\\ – 4y – 4z = 1\quad (2.1)\\4y + 4z =  – 2\quad (3.1)\end{array} \right.\) hay \(\left\{ \begin{array}{l}x + y + z = 1\quad (1)\\4y + 4z =  – 1\quad (2.1)\\4y + 4z =  – 2\quad (3.1)\end{array} \right.\)

Từ phương trình (2.1) và (3.1) suy ra -1 = -2 (Vô lí)

Vậy hệ phương trình đã cho vô nghiệm.

 

Giải bài 3 trang 24 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Tìm phương trình của parabol (P): \(y = a{x^2} + bx + c\;(a \ne 0)\) biết:

a) Parabol (P) cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x=-2; x=1 và đi qua điểm M(-1;3);

b) Parabol (P) cắt trục tung tại điểm có tung độ y=-2 và hàm số đạt giá trị nhỏ nhất bằng -4 tại x=2.

Lời giải chi tiết

a) Parabol (P) cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x=-2; x=1 hay (P) đi qua A(-2;0) và B(1;0)

\(A( – 2;0) \in (P)\) nên ta có: \(0 = a{.2^2} – b.2 + c\) hay \(4a + 2b + c = 0\)

\(B(1;0) \in (P)\) nên ta có: \(0 = a{.1^2} + b.1 + c\) hay \(a + b + c = 0\)

\(M( – 1;3) \in (P)\) nên ta có: \(3 = a.{( – 1)^2} + b.( – 1) + c\) hay \(a – b + c = 3\)

Ta có hệ phương trình:

\(\left\{ \begin{array}{l}a – b + c = 3\\4a – 2b + c = 0\\a + b + c = 0\end{array} \right.\)

Dùng máy tính cầm tay giải HPT, ta được \(a =  – \frac{3}{2},{\rm{ }}b =  – \frac{3}{2},{\rm{ }}c = 3.\)

Vậy parabol cần tìm là: \(y =  – \frac{3}{2}{x^2} – \frac{3}{2}x + 3\)

b)

Parabol (P) cắt trục tung tại điểm có tung độ y=-2 hay (P) đi qua điểm N(0;-2)

\(N(0; – 2) \in (P)\) nên ta có: \( – 2 = c\)

Hàm số đạt giá trị nhỏ nhất bằng -4 tại x=2 hay (P) đi qua điểm Q(2;-4) và \(\frac{{ – b}}{{2a}} = 2\)

\(Q(2; – 4) \in (P)\) nên ta có: \(4a + 2b – 2 =  – 4\)

\( \Rightarrow \left\{ \begin{array}{l}4a + 2b =  – 2\\b =  – 4a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b =  – 2\end{array} \right.\)

Vậy parabol cần tìm là: \(y = \frac{1}{2}{x^2} – 2x – 2\)

 

Giải bài 4 trang 24 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Một viên lam ngọc và hai viên hoàng ngọc trị giá gấp 3 lần một viên ngọc bích. Còn bảy viên lam ngọc và một viên hoàng ngọc trị giá gấp 8 lần một viên ngọc bích. Biết giá tiền của bộ ba viên ngọc này là 270 triệu đồng. Tính giá tiền mỗi viên ngọc.

Lời giải chi tiết

Gọi giá tiền mỗi viên lam ngọc, hoàng ngọc, ngọc bích là x,y, z (đơn vị triệu đồng).

Một viên lam ngọc và hai viên hoàng ngọc trị giá gấp 3 lần một viên ngọc bích hay \(x + 2y = 3z\)

Bảy viên lam ngọc và một viên hoàng ngọc trị giá gấp 8 lần một viên ngọc bích hay \(7x + y = 8z\)

Giá tiền của bộ ba viên ngọc này là 270 triệu đồng hay \(x + y + z = 270\)

Từ đó ta có hệ phương trình

\(\left\{ \begin{array}{l}x + 2y = 3z\\7x + y = 8z\\x + y + z = 270\end{array} \right.\)

Dùng máy tính cầm tay giải HPT, ta được \(x = 90,y = 90,z = 90\)

Vậy mỗi viên ngọc trị giá 90 triệu đồng.

Giải bài 5 trang 24 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Bốn ngư dân góp vốn mua chung một chiếc thuyền. Số tiền người đầu tiên đóng góp bằng một nửa tổng số tiền của những người còn lại. Người thứ hai đóng góp bằng \(\frac{1}{3}\) tổng số tiền của những người còn lại. Người thứ ba đóng góp bằng \(\frac{1}{4}\) tổng số tiển của những người còn lại. Người thứ tư đóng góp 130 triệu đồng. Chiếc thuyền này được mua giá bao nhiêu?

Lời giải chi tiết

Gọi số tiền người thứ nhất, thứ hai, thứ ba đóng góp lần lượt là x,y,z (đơn vị triệu đồng) (\(x,y,z > 0\))

Số tiền người đầu tiên đóng góp bằng một nửa tổng số tiền của những người còn lại hay \(x = \frac{{y + z + 130}}{2}\)

Người thứ hai đóng góp bằng \(\frac{1}{3}\) tổng số tiền của những người còn lại hay \(y = \frac{{x + z + 130}}{3}\)

Người thứ ba đóng góp bằng \(\frac{1}{4}\) tổng số tiển của những người còn lại hay \(z = \frac{{x + y + 130}}{4}\)

Từ đó ta có hệ phương trình

\(\left\{ \begin{array}{l}2x – y – z = 130\\x – 3y + z =  – 130\\x + y – 4z =  – 130\end{array} \right.\)

Dùng máy tính cầm tay giải HPT, ta được \(x = 200,y = 150,z = 120.\)

=> Giá của chiếc thuyền là \(200 + 150 + 120 + 130 = 600\)(triệu đồng)

Vậy chiếc thuyền có giá 600 triệu đồng.

Giải bài 6 trang 24 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Một quỹ đầu tư dự kiến dành khoản tiển 1,2 tỉ đồng để đầu tư vào cổ phiếu. Để thấy được mức độ rủi ro, các cổ phiếu được phân thành ba loại: rủi ro cao, rủi ro trung bình và rủi ro thấp. Ban Giám đốc của quỹ ước tính các cổ phiếu rủi ro cao, rủi ro trung bình và rủi ro thấp sẽ có lợi nhuận hằng năm lần lượt là 15

Lời giải chi tiết

Gọi số tiền đầu tư cổ phiếu rủi ro cao, rủi ro trung bình và rủi ro thấp là x,y,z (triệu đồng) (\(x,y,z \ge 0\))

Tổng số tiền đầu tư là 1,2 tỉ đồng = 1200 triệu đồng hay \(x + y + z = 1200\)

Lợi nhuận sau 1 năm là: \(15% x + 10% y + 6% z = 9% .1200\) hay \(0,15x + 0,1y + 0,06z = 108\)

Khoản đầu tư vào các cổ phiếu rủi ro thấp sẽ gấp đôi tổng các khoản đầu tư vào các cổ phiếu thuộc hai loại còn lại hay \(z = 2(x + y)\)

Từ đó ta có hệ phương trình:

\(\left\{ \begin{array}{l}x + y + z = 1200\\0,15x + 0,1y + 0,06z = 108\\2x + 2y – z = 0\end{array} \right.\)

Dùng máy tính cầm tay giải hệ phương trình ta được \(x = 400,y = 0,z = 800.\)

Vậy nên đầu tư 400 triệu đồng vào cổ phiếu rủi ro cao và 800 triệu đồng vào cổ phiếu rủi ro thấp. và không đầu tư vào cổ phiếu rủi ro trung bình.

Giải bài 7 trang 24 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Ba loại tế bảo A, B, C thực hiện số lần nguyên phân lần lượt là 3,4,5 và tổng số tế bào con tạo ra là 216. Biết rằng khi chưa thực hiện nguyên phân, số tế bào loại C bằng trung bình cộng số tế bào loại A và loại B. Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại B được tạo ra it hơn số tế bào con loại C được tạo ra là 40. Tính số tế bào con mỗi loại lúc ban đầu.

Lời giải chi tiết

Gọi số tế bào con mỗi loại A, B, C lúc ban đầu là x,y,z  (\(x,y,z \in \mathbb{N}\))

Ba loại tế bảo A, B, C nguyên phân lần lượt 3,4,5 lần tạo ra 216 tế bào con nên ta có \(x{.2^3} + y{.2^4} + z{.2^5} = 216\)

Khi chưa nguyên phân, số tế bào loại C bằng trung bình cộng số tế bào loại A và loại B nên ta có \(z = \frac{{x + y}}{2}\)

Tổng số tế bào con loại A và loại B được tạo ra it hơn số tế bào con loại C được tạo ra là 40 hay \(z{.2^5} = x{.2^3} + y{.2^4} + 40\)

Từ đó ta có hệ phương trình:

\(\left\{ \begin{array}{l}8x + 16y + 32z = 216\\x + y – 2z = 0\\ – 8x – 16y + 32z = 40\end{array} \right.\)

Dùng máy tính cầm tay giải hệ phương trình ta được \(x = 5,y = 3,z = 4.\)

Vậy có 5 tế bào loại A, 3 tế bào loại B và 4 tế bào loại C.

Giải bài 8 trang 25 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

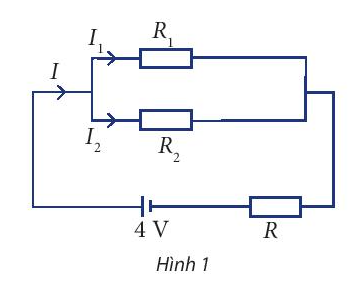
Cho sơ đồ mạch điện như Hình 1. Biết rằng \(R = {R_1} = {R_2} = 5\Omega \). Hãy tính các cường độ dòng điện \(I,{I_1}\) và \({I_2}\).

Bước 1: Lập hệ phương trình

+ Chọn ẩn và đặt điều kiện cho ẩn

+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết

+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng

Bước 2: Giải hệ phương trình

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải chi tiết

Ta có:

\(I = {I_1} + {I_2}\)

\(\begin{array}{l}{I_1}{R_1} = {I_2}{R_2} \Leftrightarrow 5{I_1} = 5{I_2} \Leftrightarrow {I_1} = {I_2}\\U + {U_1} = 4 \Leftrightarrow I.R + {I_1}{R_1} = 4 \Leftrightarrow 5I + 5{I_1} = 4\end{array}\)

Từ đó ta có hệ phương trình bậc nhất ba ẩn:

\(\left\{ \begin{array}{l} – I + {I_1} + {I_2} = 0\\{I_1} – {I_2} = 0\\5I + 5{I_1} = 4\end{array} \right.\)

Sử dụng máy tính cầm tay, ta được \(I = \frac{8}{{15}},{I_1} = \frac{4}{{15}},{I_2} = \frac{4}{{15}}\)

Vậy \(I = \frac{8}{{15}}A,{I_1} = \frac{4}{{15}}A,{I_2} = \frac{4}{{15}}A.\)

Giải bài 9 trang 25 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Cho A, B và C là ba dung dịch cùng loại acid có nồng độ khác nhau. Biết rằng nếu trộn ba dung dịch mỗi loại 100 ml thì được dung dịch nồng độ 0,4 M (mol/lít); nếu trộn 100 ml dung dịchA với 200 ml dung dịch B thì được dung dịch nồng độ 0,6 M; nếu trộn 100 ml dung dịch B với 200 ml dung dịch C thì được dung dịch nồng độ 0,3 M. Mỗi dung dịch A, B và C có nông độ bao nhiêu?

Lời giải chi tiết

Gọi nồng độ của mỗi dung dịch A, B, C lần lượt là x, y, z (M) (\(x,y,z \ge 0\))

Nếu trộn ba dung dịch mỗi loại 100 ml thì được dung dịch nồng độ 0,4 M (mol/lít) nên ta có số mol acid trong dung dịch là: \(0,1x + 0,1y + 0,1z = 0,3.0,4\)

Nếu trộn 100 ml dung dịchA với 200 ml dung dịch B thì được dung dịch nồng độ 0,6 M nên ta có số mol acid trong dung dịch là: \(0,1x + 0,2y = 0,3.0,6\)

Nếu trộn 100 ml dung dịch B với 200 ml dung dịch C thì được dung dịch nồng độ 0,3 M nên ta có số mol acid trong dung dịch là: \(0,1y + 0,2z = 0,3.0,3\)

Từ đó ta có hệ phương trình bậc nhất ba ẩn \(\left\{ \begin{array}{l}0,1x + 0,1y + 0,1z = 0,12\\0,1x + 0,2y = 0,18\\0,1y + 0,2z = 0,09\end{array} \right.\)

Dùng máy tính cầm tay, giải hpt ta được \(x = 0,4;y = 0,7;z = 0,1\)

Vậy dung dịch A có nồng độ 0,4 M; dung dịch B có nồng độ 0,7 M và dung dịch C có nồng độ 0,1 M.

Giải bài 10 trang 25 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Xăng sinh học E5 là hỗn hợp xăng không chì truyền thống và cồn sinh học (bio -ethanol). Trong loại xăng này chứa 5

.

Cân bằng phương trình hóa học trên.

Bước 1: Lập hệ phương trình

+ Chọn ẩn và đặt điều kiện cho ẩn

+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết

+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng

Bước 2: Giải hệ phương trình

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.

Lời giải chi tiết

Giả sử x, y, z, t là các số nguyên dương thỏa mãn cân bằng phương trình phản ứng hóa học:

 

Số nguyên tử hydrogen ở hai vế bằng nhau, ta có: \(6x = 2t \Leftrightarrow t = 3x\)

Số nguyên tử oxygen ở hai vế bằng nhau, ta có: \(x + 2y = 2z + t\)

Số nguyên tử carbon ở hai vế bằng nhau, ta có: \(2x = z\)

Từ đó ta có hệ phương trình:

\(\left\{ \begin{array}{l}x + 2y = 2z + t\\z = 2x\\t = 3x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 + 2\frac{y}{x} = 2\frac{z}{x} + 3\\\frac{z}{x} = 2\\\frac{t}{x} = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{y}{x} = 3\\\frac{z}{x} = 2\\\frac{t}{x} = 3\end{array} \right.\)

Để phương trình có hệ số đơn giản, ta chọn \(x = 1\), ta có \(y = 3,z = 2,t = 3\)

Vậy phương trình cân bằng phản ứng hóa học là

Giải bài 11 trang 25 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Trên thị trường hàng hoá có ba loại sản phẩmA, B, C với giá mỗi tấn tương úng là x, y, z (đơn vị: triệu đồng,\(x \ge 0,{\rm{ }}y \ge 0,z \ge 0\)). Lượng cung và lượng cầu của mỗi sản phẩm được cho trong bảng dưới đây:

Tìm giá của mỗi sản phẩm để thị trường cân bằng.

Lời giải chi tiết

Để tìm giá của mỗi sản phẩm A, B, C, ta xét hệ phương trình

\(\left\{ \begin{array}{l}{Q_{{S_A}}} = {Q_{{D_A}}}\\{Q_{{S_B}}} = {Q_{{D_B}}}\\{Q_{{S_C}}} = {Q_{{D_C}}}\end{array} \right.\) tức là \(\left\{ \begin{array}{l} – 60 + 4x – 2z = 137 – 3x + y\\ – 30 – x + 5y – z = 131 + x – 4y + z\\ – 30 – 2x + 3z = 157 + y – 2z\end{array} \right.\) hay \(\left\{ \begin{array}{l}7x – y – 2z = 197\\ – 2x + 9y – 2z = 161\\ – 2x – y + 5z = 187\end{array} \right.\)

Sử dụng máy tính cầm tay giải hệ phương trình, ta được: \(x = 54;y = 45;z = 68\)

Vậy để thị trường cân bằng thì sản phẩm A giá 54 triệu đồng, sản phẩm B giá 45 triệu đồng và sản phẩm C giá 68 triệu đồng

Giải bài 12 trang 25 Chuyên đề học tập Toán 10 – Chân trời sáng tạo

Đề bài

Giải bài toán cố sau:

Trăm trâu, trăm cỏ

Trâu đứng ăn năm

Trâu nằm ăn ba

Lụ khụ trâu già

Ba con một bó

Hỏi có bao nhiêu con trâu đứng, trâu nằm, trâu già?

Lời giải chi tiết

Gọi số trâu đứng, trâu nằm, trâu già lần lượt là x, y, z (con) (\(x,y,z \in \mathbb{N}*\))

Tổng số trâu là \(x + y + z = 100\)

Tổng số bó cỏ mà trâu đã ăn là \(5x + 3y + \frac{1}{3}z = 100\)

Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}x + y + z = 100\\5x + 3y + \frac{1}{3}z = 100\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y + z = 100\\15x + 9y + z = 300\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x + y + z = 100\\14x + 8y = 200\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y + z = 100\\14x = 200 – 8y\end{array} \right.\)

Vì \(x,y \in \mathbb{N}*\) nên \(14x < 200 \Leftrightarrow x \le 14\)

Mà \(200 – 8x \vdots 8 \Rightarrow 14x \vdots 8 \Leftrightarrow x \vdots 4\)

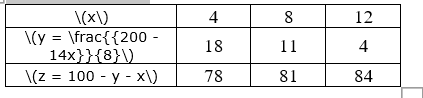
Ta có bảng giá trị

Vậy:

nếu trâu đứng có 4 con thì trâu nằm có 18 con và trâu già có 78 con;

nếu trâu đứng có 8 con thì trâu nằm có 11 con và trâu già có 81 con;

nếu trâu đứng có 12 con thì trâu nằm có 4 con và trâu già có 84 con.