Giải bài tập Bài 4: Tích vô hướng của hai vectơ (Chân trời)

Giải bài tập Bài 4: Tích vô hướng của hai vectơ (Chân trời)

===========

Giải bài 1 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1

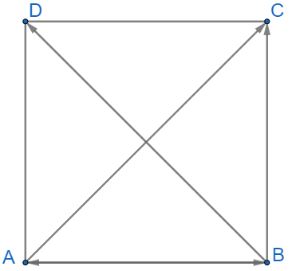
Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng:

\(\overrightarrow {AB} .\overrightarrow {AD} ,\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {CB} ,\overrightarrow {AC} .\overrightarrow {BD} \)

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Bước 1: Sử dụng công thức \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)

Bước 2: Tính \(\left| {\overrightarrow a } \right|,\left| {\overrightarrow b } \right|\) và góc \(\left( {\overrightarrow a ,\overrightarrow b } \right)\)

Lời giải chi tiết

Ta có: \(AC = BD = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \)

+) \(AB \bot AD \Rightarrow \overrightarrow {AB}  \bot \overrightarrow {AD}  \Rightarrow \overrightarrow {AB} .\overrightarrow {AD}  = 0\)

+) \(\overrightarrow {AB} .\overrightarrow {AC}  = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a.\cos 45^\circ  = \frac{{{a^2}\sqrt 2 }}{2}\)

+) \(\overrightarrow {AC} .\overrightarrow {CB}  = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a\sqrt 2 .a.\cos 135^\circ  =  – {a^2}\)

+) \(AC \bot BD \Rightarrow \overrightarrow {AC}  \bot \overrightarrow {BD}  \Rightarrow \overrightarrow {AC} .\overrightarrow {BD}  = 0\)

Chú ý

\(\overrightarrow {a}  \bot \overrightarrow {b}  \Leftrightarrow \overrightarrow {a} .\overrightarrow {b}  = 0\)

---

Giải bài 2 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 – CTST

Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:

a) \(\overrightarrow {AB} .\overrightarrow {AO} \);

b) \(\overrightarrow {AB} .\overrightarrow {AD} \).

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

a) Bước 1: Tính đường chéo AC, BD

Bước 2: Xác định số đo góc \(\widehat {OAB}\)

Bước 3: Sử dụng công thức \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)

b) Sử dụng công thức \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)

Lời giải chi tiết

a) \(AC = BD = \sqrt {A{B^2} + A{D^2}}  \\= \sqrt {{{\left( {2a} \right)}^2} + {a^2}}  = a\sqrt 5 \)

\(\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right) = \cos \widehat {OAB} =\\ \cos \widehat {CAB} = \frac{{AB}}{{AC}} = \frac{{2a}}{{a\sqrt 5 }} = \frac{{2\sqrt 5 }}{5}\)

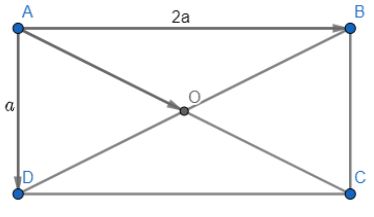
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AO}  = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AO} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right) \\= AB.\frac{1}{2}AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right)\\ = 2a.\frac{1}{2}.a\sqrt 5 .\frac{{2\sqrt 5 }}{5} = 2{a^2}\end{array}\)

b) \(AB \bot AD \Rightarrow \overrightarrow {AB}  \bot \overrightarrow {AD}  \Rightarrow \overrightarrow {AB} .\overrightarrow {AD}  = 0\)

---

Giải bài 3 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1

Cho ba điểm O, A, B thẳng hàng và OA=a, OB=b. Tính tích vô hướng \(\overrightarrow {OA} .\overrightarrow {OB} \) trong hai trường hợp:

a)  Điểm O nằm ngoài đoạn thẳng AB;

b) Điểm O nằm trong đoạn thẳng AB

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Bước 1: Xác định góc giữa hai vectơ: \(\overrightarrow a \)và \(\overrightarrow b \) cùng hướng thì \(\left( {\overrightarrow a ,\overrightarrow b } \right) = 0^\circ \)

Nếu \(\overrightarrow a \)và \(\overrightarrow b \) ngược hướng thì \(\left( {\overrightarrow a ,\overrightarrow b } \right) = 180^\circ \)

Bước 2: Sử dụng công thức \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)

Lời giải chi tiết

a) Ta có:

Ta thấy hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) cùng hướng nên \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = 0^\circ \)

\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB}  = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = a.b.\cos 0^\circ  = ab\)

b) Ta có:

Ta thấy hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) ngược hướng nên \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = 180^\circ \)

\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB}  = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = a.b.\cos 180^\circ  =  – ab\)

---

Giải bài 4 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1

Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng:

\(\overrightarrow {MA} .\overrightarrow {MB}  = {\overrightarrow {MO} ^2} – {\overrightarrow {OA} ^2}\)

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

Sử dụng hằng đẳng thức \({a^2} – {b^2} = \left( {a – b} \right)\left( {a + b} \right)\) phân tích \({\overrightarrow {MO} ^2} – {\overrightarrow {OA} ^2}\)

Lời giải chi tiết

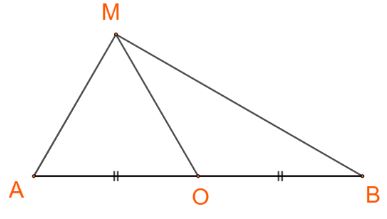
Ta có: \(\overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow 0  \Leftrightarrow  – \overrightarrow {OA}  = \overrightarrow {OB} \)

\(\Rightarrow {\overrightarrow {MO} ^2} – {\overrightarrow {OA} ^2} = \left( {\overrightarrow {MO}  – \overrightarrow {OA} } \right)\left( {\overrightarrow {MO}  + \overrightarrow {OA} } \right) \\= \left( {\overrightarrow {MO}  + \overrightarrow {OB} } \right)\left( {\overrightarrow {MO}  + \overrightarrow {OA} } \right) = \overrightarrow {MB} .\overrightarrow {MA} \) (đpcm)

---

Giải bài 5 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1

Một người dùng một lực \(\overrightarrow F \) có độ lớn là 90 N làm một vật dịch chuyển một đoạn 100 m. Biết lực hợp \(\overrightarrow F \) với hướng dịch chuyển là một góc \(60^\circ \). Tính công sinh bởi lực \(\overrightarrow F \)

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

Sử dụng công thức tính công: \(A = \overrightarrow F .\overrightarrow d \)

Lời giải chi tiết

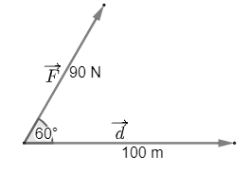
Công sinh bởi lực \(\overrightarrow F \) được tính bằng công thức

\(A = \overrightarrow F .\overrightarrow d  = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 90.100.\cos 60^\circ  = 4500\) (J)

Vậy công sinh bởi lực \(\overrightarrow F \) có độ lớn bằng 4500 (J)

---

Giải bài 6 trang 101 SGK Toán 10 Chân trời sáng tạo tập 1 – CTST

Cho hai vectơ có độ dài lần lượt là 3 và 4 có tích vô hướng là \( – 6\). Tính góc giữa hai vectơ đó.

Hướng dẫn giải chi tiết Bài 6

Phương pháp giải

Sử dụng công thức \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)

Lời giải chi tiết

Ta cho: \(\left| {\overrightarrow a } \right| = 3;\left| {\overrightarrow b } \right| = 4\) và \(\overrightarrow a .\overrightarrow b  =  – 6\)

Ta có công thức:

\(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 3.4.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)

\(\overrightarrow a .\overrightarrow b  =  – 6 \Rightarrow 3.4.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) =  – 6 \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) =  – \frac{1}{2}\)

\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 120^\circ \)