Giải bài tập Bài 1 Bất phương trình bậc nhất hai ẩn (Cánh diều)

Giải bài tập Bài 1 Bất phương trình bậc nhất hai ẩn (Cánh diều)

============

 

Giải câu 1 bài bất phương trình bậc nhất hai ẩn

 

Bài tập 1.  Cặp số nào sau đây là nghiệm của bất phương trình $2 x-3 y<3$?

a. $(0 ;-1)$;

b. $(2 ; 1)$;

c. $(3 ; 1)$.

Bài giải:

a. Thay $x=0;y=-1$, ta có: $2.0-3.(-1)=3<3$ là mệnh đề sai.

Vậy $(0 ;-1)$ không là nghiệm của bất phương trình $2 x-3 y<3$.

b. Thay $x=2;y=1$, ta có: $2.2-3.1=1<3$ là mệnh đề đúng.

Vậy $(2 ;1)$ là nghiệm của bất phương trình $2 x-3 y<3$.

c. Thay $x=3;y=1$, ta có: $2.3-3.1=3<3$ là mệnh đề sai.

Vậy $(3 ;1)$ không là nghiệm của bất phương trình $2 x-3 y<3$.

Giải câu 2 bài bất phương trình bậc nhất hai ẩn

 

Bài tập 2.  Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a. $x+2 y<3$;

b. $3 x-4 y \geq-3$;

c. $y \geq-2 x+4$;

d. $y<1-2 x$.

Bài giải:

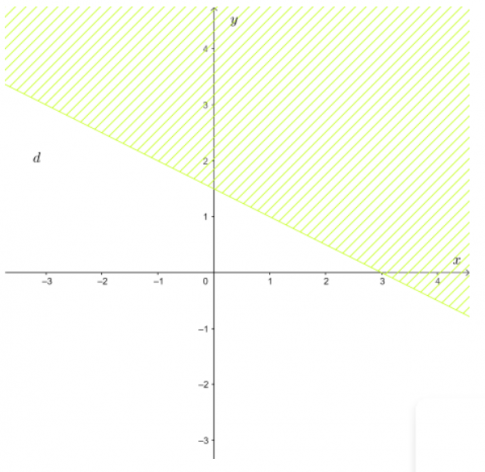
a. $x+2 y<3$

• Vẽ đường thẳng $d:x+2y=3$
• Lấy điểm $O(0;0)$. Ta có $0+2.0=2<3$.
• Vậy miền nghiệm của bất phương trình $x+2y<3$ là nửa mặt phẳng không bị gạch chứa điểm $O(0;0)$ không kể đường thẳng $d$.

b. $3 x-4 y \geq-3$

• Vẽ đường thẳng $d:3 x-4 y=-3$
• Lấy điểm $O(0;0)$. Ta có $3.0-4.0=0>-3$.
• Vậy miền nghiệm của bất phương trình $3 x-4 y \geq-3$ là nửa mặt phẳng không bị gạch chứa điểm $O(0;0)$ kể cả đường thẳng $d$.

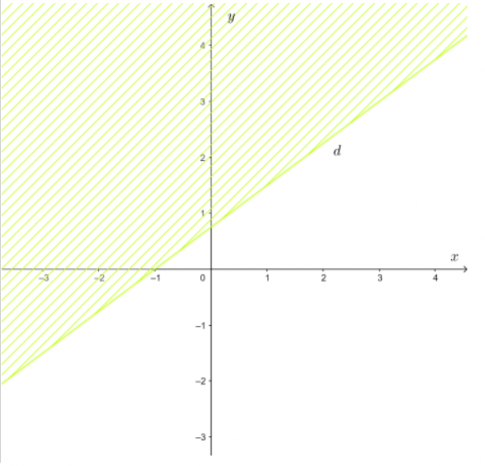
c. $y \geq-2 x+4$

• Vẽ đường thẳng $d:y=-2 x+4$
• Lấy điểm $O(0;0)$. Ta có $0=-2.0+4$ (vô lý).
• Vậy miền nghiệm của bất phương trình $y \geq-2 x+4$ là nửa mặt phẳng không bị gạch không chứa điểm $O(0;0)$ kể cả đường thẳng $d$.

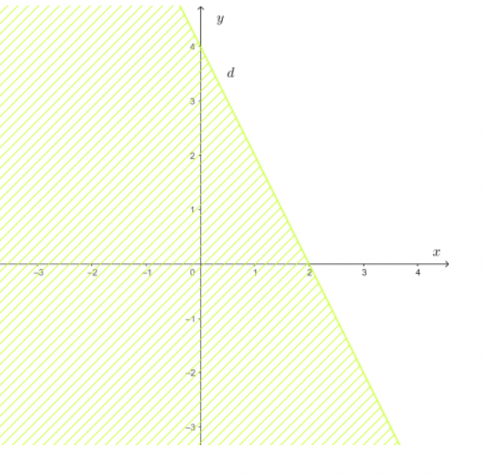
d. $y<1-2 x$

• Vẽ đường thẳng $d:y=1-2 x$
• Lấy điểm $O(0;0)$. Ta có $0<1-2.0$.
• Vậy miền nghiệm của bất phương trình $y \geq-2 x+4$ là nửa mặt phẳng không bị gạch chứa điểm $O(0;0)$ không kể đường thẳng $d$.

Giải câu 3 bài bất phương trình bậc nhất hai ẩn

 

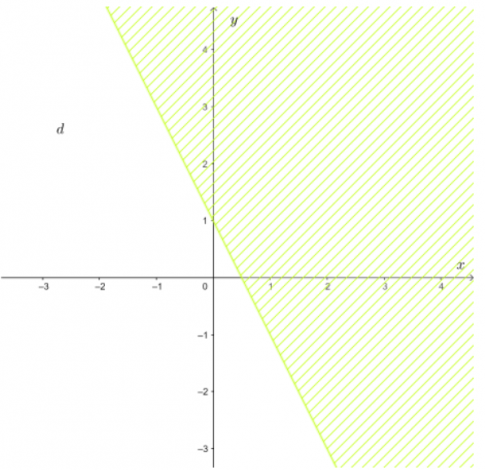
Bài tập 3.  Nửa mặt phẳng không bị gạch (không kể đường thẳng $d$ ) ở mỗi Hình $7a, 7b, 7c$ là miền nghiệm của bất phương trình nào?

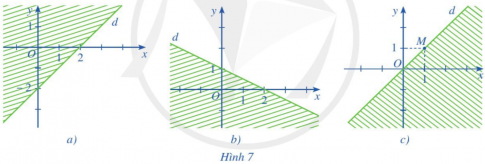
Bài giải:

a. Gọi phương trình đường thẳng $d$ là $y=ax+b (a\neq 0)$.

$d$ đi qua $(2;0)$ và $(0;-2)$ nên ta có $\left\{\begin{array}{l}0=a.2+b \\ -2=a.0+b\end{array}\right.$ $\Leftrightarrow$ $\left\{\begin{array}{l}a=1 \\b=-2\end{array}\right.$

$\Rightarrow d: y=x -2$

Lấy điểm $O(3;0)$ thuộc miền nghiệm, ta có $0<3-2$.

Vậy bất phương trình cần tìm là $y<x -2$

b. Gọi phương trình đường thẳng $d$ là $y=ax+b (a\neq 0)$.

$d$ đi qua $(2;0)$ và $(0;1)$ nên ta có $\left\{\begin{array}{l}0=a.2+b \\ 1=a.0+b\end{array}\right.$ $\Leftrightarrow$ $\left\{\begin{array}{l}a=\frac{-1}{2} \\b=1\end{array}\right.$

$\Rightarrow d: y=\frac{-1}{2}x +1$

Lấy điểm $O(3;0)$ thuộc miền nghiệm, ta có $0>\frac{-1}{2}.3 +1$.

Vậy bất phương trình cần tìm là $y>\frac{-1}{2}x +1$

c. $d$ đi qua $(0;0)$ và $(1;1)$ nên $d: x-y=0$

Lấy điểm $O(-1;0)$ thuộc miền nghiệm, ta có $-1-0<0$.

Vậy bất phương trình cần tìm là $x-y<0$

Giải câu 4 bài bất phương trình bậc nhất hai ẩn

 

Bài tập 4.  Một gian hàng trưng bày bàn và ghế rộng $60 \mathrm{~m}^{2}$. Diện tích để kê một chiếc ghế là $0,5 \mathrm{~m}^{2}$, một chiếc bàn là $1,2 \mathrm{~m}^{2}$. Gọi $x$ là số chiếc ghế, $y$ là số chiếc bàn được kê.

a. Viết bất phương trình bậc nhất hai ẩn $x, y$ cho phần mặt sàn để kê bàn và ghế, biết diện tích mặt sàn dành cho lưu thông tối thiểu là $12 \mathrm{~m}^{2}$.

b. Chỉ ra ba nghiệm của bất phương trình trên.

Bài giải:

a.

• Diện tích để kê $x$ chiếc ghế là $0,5x \mathrm{~m}^{2}$ và diện tích để kê $y$ chiếc bàn là $1,2y \mathrm{~m}^{2}$.
• Diện tích mặt sàn dành cho lưu thông là $60-0,5x-1,2y$

Vậy ta có bất phương trình $60-0,5x-1,2y \geq 12 \Leftrightarrow 0,5x+1,2y \leq 48$.

b.

• Chọn $x=10, y=10$, ta có: $0,5.10+1,2.10=5+12=17 \leq 48$ là mệnh đề đúng.

Vậy $(10;10)$ là nghiệm của bất phương trình.

• Chọn $x=10, y=20$, ta có: $0,5.10+1,2.20=5+24=29 \leq 48$ là mệnh đề đúng.

Vậy $(10;20)$ là nghiệm của bất phương trình.

• Chọn $x=20, y=20$, ta có: $0,5.20+1,2.20=10+24=34 \leq 48$ là mệnh đề đúng.

Vậy $(20;20)$ là nghiệm của bất phương trình.

Giải câu 5 bài bất phương trình bậc nhất hai ẩn

 

Bài tập 5.  Trong 1 lạng $(100 \mathrm{~g})$ thịt bò chứa khoảng $26 \mathrm{~g}$ protein, 1 lạng cá rô phi chứa khoảng $20 \mathrm{~g}$ protein. Trung bình trong một ngày, một người phụ nữ cần tối thiểu $46 \mathrm{~g}$ protein (Nguồn: https://vinmec.com và https://thanhnien.vn).

Gọi $x, y$ lần lượt là số lạng thịt bò và số lạng cá rô phi mà một người phụ nữ nên ăn trong một ngày. Viết bất phương trình bậc nhất hai ẩn $x, y$ để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày và chỉ ra ba nghiệm của bất phương trình đó.

Bài giải:

a. Trong $x$ lạng thịt bò chứa $26x \mathrm{~g}$ protein, $y$ lạng cá rô phi chứa $20y \mathrm{~g}$ protein

Tổng lượng protein trong $x$ lạng thịt bò và $y$ lạng cá rô phi là:

$26.x+20.y$

Vậy bất phương trình cần tìm là $26.x+20.y \geq 46$.

b.

• Chọn $x=1, y=1$, ta có: $26.1+20.1 =46 \geq 46$ là mệnh đề đúng.

Vậy $(1;1)$ là nghiệm của bất phương trình.

• Chọn $x=1, y=2$, ta có: $26.1+20.2 =66 \geq 46$ là mệnh đề đúng.

Vậy $(1;2)$ là nghiệm của bất phương trình.

• Chọn $x=1, y=3$, ta có: $26.1+20.3=86 \geq 46$ là mệnh đề đúng.

Vậy $(1;3)$ là nghiệm của bất phương trình.