Giải bài 1 trang 21 Chuyên đề học tập Toán 10 – Cánh diều>
Đề bài
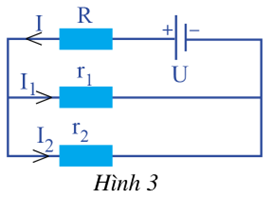
Cho mạch điện như Hình 3. Biết \(U = 20V,R = 0,5\Omega ,\;{r_1} = 1\Omega ,{r_2} = 2\Omega .\) Tìm cường độ dòng điện \({I_1},{I_2},I\) chạy qua mỗi điện trở.

Lời giải chi tiết
Ta có:
\(\left\{ \begin{array}{l}U = RI\\{r_1}{I_1} = {r_2}{I_2}\\I = {I_1} + {I_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}20 = 0,5.I\\1.{I_1} = 2.{I_2}\\{I_1} + {I_2} – I = 0\end{array} \right.\)
Giải hệ bằng máy tính cầm tay ta được: \(I = 40,{I_1} = \frac{{80}}{3},{I_2} = \frac{{40}}{3}\)
Giải bài 1 trang 21 Chuyên đề học tập Toán 10 – Cánh diều>
Giải bài 2 trang 21 Chuyên đề học tập Toán 10 – Cánh diều>
Đề bài
Cho mạch điện như Hình 4. Biết
a) Tính điện trở của mỗi bóng đèn.
b) Tính cường độ dòng điện chạy qua mỗi bóng đèn và điện trở R.
Lời giải chi tiết
a) Điện trở của bóng đèn 1 là: \({R_1} = \frac{{{{12}^2}}}{6} = 24\left( \Omega \right)\)
Điện trở của bóng đèn 2 là: \({R_2} = \frac{{{{12}^2}}}{{12}} = 12\left( \Omega \right)\)
b) Gọi cường độ dòng điện chạy qua bóng đèn 1, bóng đèn 1 và điện trở R là \({I_1},{I_2},I\)
Ta có: \(\left\{ \begin{array}{l}U = RI\\{R_1}{I_1} = {R_2}{I_2}\\I = {I_1} + {I_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}24 = 3I\\24{I_1} = 12{I_2}\\I = {I_1} + {I_2}\end{array} \right.\)
Giải hệ bằng máy tính cầm tay ta được: \(I = 8,{I_1} = \frac{8}{3},{I_2} = \frac{{16}}{3}\)
Giải bài 2 trang 21 Chuyên đề học tập Toán 10 – Cánh diều
Giải bài 3 trang 22 Chuyên đề học tập Toán 10 – Cánh diều>
Đề bài
Tìm các hệ số x, y, z để cân bằng mỗi phương trình phản ứng hóa học sau:
a)
b) \(xFeC{l_2} + yC{l_2} \to zFeC{l_3}\)
c)
d)
Lời giải chi tiết
a) Theo định luật bảo toàn nguyên tố đối với K, Cl và O ta có: \(x = y\) hay \(x – y = 0\) và \(3x = 2z\) hay \(3x – 2z = 0\)
Ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}x – y = 0\\3x – 2z = 0\end{array} \right.\)
Chọn \(x = 2\). Khi đó hệ trở thành \(\left\{ \begin{array}{l}x = 2\\2 – y = 0\\3.2 – 2z = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 2\\z = 3\end{array} \right.\)
Vậy ta có phương trình sau cân bằng:
b) Theo định luật bảo toàn nguyên tố đối với Fe và Cl ta có: \(x = z\) hay \(x – z = 0\) và \(2x + 2y = 3z\) hay \(2x + 2y – 3z = 0\)
Ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}x – z = 0\\2x + 2y – 3z = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x – z = 0\\2y – z = 0\end{array} \right. \Leftrightarrow x = 2y = z\)
Chọn \(x = 2\). Khi đó \(x = 2,y = 1,z = 2\)
Vậy ta có phương trình sau cân bằng: \(2FeC{l_2} + C{l_2} \to 2FeC{l_3}\)
c) Theo định luật bảo toàn nguyên tố đối với Fe và O ta có: \(x = 2z\) hay \(x – 2z = 0\) và \(2y = 3z\) hay \(2y – 3z = 0\)
Ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}x – 2z = 0\\2y – 3z = 0\end{array} \right.\)
Chọn \(y = 3\). Khi đó Khi đó hệ trở thành \(\left\{ \begin{array}{l}y = 3\\x – 2z = 0\\2.3 – 3.z = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\\x – 2z = 0\\z = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 3\\x = 4\\z = 2\end{array} \right.\)
Vậy ta có phương trình sau cân bằng:
d) Theo định luật bảo toàn nguyên tố
+ đối với Na ta có: \(2x + y = 2z\) hay \(2x + y – 2z = 0\)
+ đối với S ta có: \(x + y = z + 2 + 1\) hay \(x + y – z = 3\)
+ đối với O ta có: \(3x + 8 + 4y = 4z + 8 + 4 + 3\) hay \(3x + 4y – 4z = 7\)
Ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}2x + y – 2z = 0\\x + y – z = 3\\3x + 4y – 4z = 7\end{array} \right.\)
Giải hệ bằng máy tính cầm tay, ta được \(x = 5,y = 6,z = 8\)
Vậy ta có phương trình sau cân bằng:
Giải bài 3 trang 22 Chuyên đề học tập Toán 10 – Cánh diều
Giải bài 4 trang 22 Chuyên đề học tập Toán 10 – Cánh diều>
Đề bài
Một giáo viên dạy Hóa tạo 1000g dung dịch HCl 25
Phương pháp giải
Bước 1: Lập hệ phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải chi tiết
Gọi khối lượng dung dịch HCl 10
Ta có:
Khối lượng dung dịch thu được là 1000g, hay \(x + y + z = 1000\)
Khối lượng HCl trong dung dịch là: \(25% .1000 = 10% .x + 20% .y + 30% .z\) hay \(250 = 0,1x + 0,2y + 0,3z\)
Lượng HCl có trong dung dịch 10
Từ đó ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y + z = 1000\\0,1x + 0,2y + 0,3z = 250\\0,1x – 0,05y = 0\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \({I_1} = \frac{{11}}{{28}},{I_2} = \frac{2}{7},{I_3} = \frac{{19}}{{28}}\)
Vậy \({I_1} = \frac{{11}}{{28}}A,{I_2} = \frac{2}{7}A,{I_3} = \frac{{19}}{{28}}A\)
Giải bài 4 trang 22 Chuyên đề học tập Toán 10 – Cánh diều
Giải bài 5 trang 22 Chuyên đề học tập Toán 10 – Cánh diều>
Đề bài
Tổng số hạt p, n, e trong hai nguyên tử kim loại A và B là 177. Trong đó số hạt mang điện nhiều hơn số hạt không mang điện là 47. Số hạt mang điện của nguyên tử B nhiều hơn của nguyên tử A là 8. Xác định số hạt proton trong một nguyên tử A.
Phương pháp giải
Bước 1: Lập hệ phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải chi tiết
Gọi \({Z_A},{N_A}\) lần lượt là số lượng hạt p, n của nguyên tử A;
\({Z_B},{N_B}\) lần lượt là số lượng hạt p, n của nguyên tử B.
Theo giả thiết, tổng số hạt p, n, e là 177 nên ta có:
\(2{Z_A} + {N_A} + 2{Z_B} + {N_B} = 177\)
Do số hạt mang điện nhiều hơn số hạt không mang điện là 47 nên ta có:
\(\left( {2{Z_A} + 2{Z_B}} \right) – \left( {{N_A} + {N_B}} \right) = 47\)
Số hạt mang điện của nguyên tử B nhiều hơn của nguyên tử A là 8 nên ta có:
\(2{Z_B} – 2{Z_A} = 8\)
Đặt \(N = {N_A} + {N_B}\), ta được hệ phương trình:
\(\left\{ \begin{array}{l}2{Z_A} + 2{Z_B} + N = 177\\2{Z_A} + 2{Z_B} – N = 47\\ – 2{Z_A} + 2{Z_B} = 8\end{array} \right.\)
Dùng máy tính cầm tay giải hệ, ta được \({Z_A} = 26;{Z_B} = 30;N = 65\)
Vậy số hạt proton trong một nguyên tử A là 26.
Giải bài 5 trang 22 Chuyên đề học tập Toán 10 – Cánh diều
Giải bài 6 trang 22 Chuyên đề học tập Toán 10 – Cánh diều>
Đề bài
Một phân tử DNA có khối lượng là \({72.10^4}\) đvC và có 2826 liên kết hyddro. Mạch 2 có số nu loại A bằng 2 lần số nu loại T và bằng 3 lần số nu loại X. Xác định số nucleotit mỗi loại trên từng mạch của phân tử DNA đó. Biết rằng một nu có khối lượng trung bình là 300 đvC.
Lời giải chi tiết
Kí hiệu: A, G, T, X lần lượt là tổng số nu loại A, G, T, X của phân tử DNA.
N là tổng số nu của phân tử DNA
\({A_1},{G_1},{T_1},{X_1}\) lần lượt là tổng số nu loại A, G, T, X trong mạch 1.
\({A_2},{G_2},{T_2},{X_2}\) lần lượt là tổng số nu loại A, G, T, X trong mạch 2.
Ta có: Khối lượng DNA là \({72.10^4}\) đvC
\( \Rightarrow N = {72.10^4}:300 = 2400\) hay \(2A + 2G = 2400\) (1)
Lại có: Số liên kết hyddro là 2826 liên kết \( \Rightarrow 2A + 3G = 2826\) (2)
Từ (1,2) ta suy ra \(A = T = 774\) và \(G = X = 426\)
Mạch 2 có số nu loại A bằng 2 lần số nu loại T và bằng 3 lần số nu loại X
\( \Rightarrow {A_2} = 2{T_2} = 3{X_2}\)
Mà \(A = {A_1} + {A_2} = {T_2} + 2{T_2} = 3{T_2} \Rightarrow {T_2} = 774:3 = 258\)
\( \Rightarrow {A_2} = 2.258 = 516;\;\;{X_2} = 516:3 = 172\)
\(G = {G_1} + {G_2} = {X_2} + {G_2} \Rightarrow {G_2} = 426 – 172 = 254\)
Vậy số nucleotit trên mỗi loại trên từng mạch của phân tử DNA đó là:
\({A_1} = {T_2} = 258;\;\;{T_1} = {A_2} = 516;\;\;{G_1} = {X_2} = 172;\;\;{X_1} = {G_2} = 254.\)
Giải bài 6 trang 22 Chuyên đề học tập Toán 10 – Cánh diều
Giải bài 7 trang 22 Chuyên đề học tập Toán 10 – Cánh diều>
Đề bài
Tìm đa thức bậc ba \(f(x) = a{x^3} + b{x^2} + cx + 1\) (với \(a \ne 0\)) biết \(f( – 1) = – 2,f(1) = 2,f(2) = 7\).
Lời giải chi tiết
Theo giải thiết ta có:
\(f( – 1) = – 2 \Rightarrow – 2 = a.{( – 1)^3} + b.{( – 1)^2} + c.( – 1) + 1\)
\(f(1) = 2 \Rightarrow 2 = a{.1^3} + b{.1^2} + c.1 + 1\)
\(f(2) = 7 \Rightarrow 7 = a{.2^3} + b{.2^2} + c.2 + 1\)
Rút gọn ta được hệ phương trình
\(\left\{ \begin{array}{l} – a + b – c = – 3\\a + b + c = 1\\8a + 4b + 2c = 6\end{array} \right.\)
Dùng máy tính cầm tay, giải hpt ta được \(a = 1,b = – 1,c = 1\)
Vậy đa thức cần tìm là \(f(x) = {x^3} – {x^2} + x + 1\).
Giải bài 7 trang 22 Chuyên đề học tập Toán 10 – Cánh diều
Giải bài 8 trang 22 Chuyên đề học tập Toán 10 – Cánh diều>
Đề bài
Ba lớp 10A, 10B, 10C trồng được 164 cây bạch đàn và 316 cây thông. Mỗi học sinh lớp 10A trồng được 3 cây bạch đàn và 2 cây thông; mỗi học sinh lớp 10B trồng được 2 cây bạch đàn và 3 cây thông; mỗi học sinh lớp 10C trồng được 5 cây thông. Hỏi mỗi lớp có bao nhiêu học sinh? Biết số học sinh lớp 10A bằng trung bình cộng số học sinh lớp 10B và 10C.
Lời giải chi tiết
Gọi số học sinh lớp 10A, 10B, 10C lần lượt là x, y, z \((x,y,z \in \mathbb{N})\)
Tổng số cây bạch đàn trồng được là 164 cây nên ta có \(3x + 2y + 0z = 164\)
Tổng số cây thông trồng được là 316 cây nên ta có \(2x + 3y + 5z = 316\)
Do số học sinh lớp 10A bằng trung bình cộng số học sinh lớp 10B và 10C nên ta có: \(x = \frac{{y + z}}{2}\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}3x + 2y + 0z = 164\\2x + 3y + 5z = 316\\2x – y – z = 0\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \(x = 32;y = 34;z = 30\)
Vậy lớp 10A có 32 học sinh, lớp 10B có 34 học sinh và lớp 10C có 30 học sinh.
Giải bài 8 trang 22 Chuyên đề học tập Toán 10 – Cánh diều
Giải bài 9 trang 22 Chuyên đề học tập Toán 10 – Cánh diều>
Đề bài
Độ cao h trong chuyển động của một vật được tính bởi công thức \(h = \frac{1}{2}a{t^2} + {v_0}t + {h_0}\), với độ cao h và độ cao ban đầu \({h_0}\) được tính bằng mét, t là thời gian của chuyển động tính bằng giây, a là gia tốc của chuyển động tính bằng \(m/{s^2}\), \({v_0}\) là vận tốc ban đầu tính bằng m/s. Tìm \(a,{v_0},{h_0}.\) Biết rằng sau 1s và 3s vật cùng đạt được độ cao 50,225m; sau 2s vật đạt độ cao 55,125m.
Lời giải chi tiết
Độ cao h sau 1s là 50,225m nên ta có: \(50,225 = \frac{1}{2}a{.1^2} + {v_0}.1 + {h_0}\)
Độ cao h sau 3s là 50,225m nên ta có: \(50,225 = \frac{1}{2}a{.3^2} + {v_0}.3 + {h_0}\)
Độ cao h sau 2s là 55,125m nên ta có: \(55,125 = \frac{1}{2}a{.2^2} + {v_0}.2 + {h_0}\)
Từ đó ta có hệ phương trình:
\(\left\{ \begin{array}{l}\frac{1}{2}a + {v_0} + {h_0} = 50,225\\\frac{9}{2}a + 3{v_0} + {h_0} = 50,225\\2a + 2{v_0} + {h_0} = 55,125\end{array} \right.\)
Sử dụng máy tính cầm tay, ta được \(a = – 9,8;{v_0} = 19,6;{h_0} = 35,525\)
Vậy \(a = – 9,8;{v_0} = 19,6;{h_0} = 35,525\)
Giải bài 9 trang 22 Chuyên đề học tập Toán 10 – Cánh diều
Giải bài 10 trang 22 Chuyên đề học tập Toán 10 – Cánh diều>
Đề bài
Một ngân hàng muốn đầu tư số tiền tín dụng là 100 tỉ đồng thu được vào ba nguồn: mua trái phiếu với mức sinh lời 8
Phương pháp giải
Bước 1: Lập hệ phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết
+ Lập các phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận.
Lời giải chi tiết
Giả sử x, y, z là số tiền đầu tư trái phiếu, cho vay và đầu tư bất động sản. (đơn vị tỉ đồng)
Tổng số tiền đầu tư là 100 tỉ đồng hay \(x + y + z = 100\)
Vì tổng số tiền đầu tư vào trái phiếu và cho vay phải gấp ba lần số tiền đầu tư vào bất động sản nên \(x + y = 3z\)
Ngân hàng muốn thu được 9,6 tỉ đồng hằng năm hay \(8% x + 10% y + 12% z = 9,6\)
Ta có hệ phương trình \(\left\{ \begin{array}{l}x + y + z = 100\\x + y – 3z = 0\\0,08x + 0,1y + 0,12z = 9,6\end{array} \right.\)
Dùng máy tính cầm tay, ta suy ra \(x = 45,y = 30,z = 25\)
Vậy ngân hàng nên đầu tư 45 tỉ mua trái phiếu, cho vay 30 tỉ và đầu tư bất động sản 25 tỉ.
Giải bài 10 trang 22 Chuyên đề học tập Toán 10 – Cánh diều
