Đề bài
Câu 1 (1,5 điểm). Tìm tập xác định của hàm số
\(y = \dfrac{{\sqrt { – {x^2} + 5x – 4} }}{{x – 2}}.\)
Câu 2 (2 điểm).
1. Tính giá trị của biểu thức
\(A = \cos \dfrac{{2\pi }}{5} + \cos \dfrac{{4\pi }}{5} + \cos \dfrac{{6\pi }}{5} \)\(\,+ \cos \dfrac{{8\pi }}{5}.\)
2. Chứng minh rằng
\({\sin ^4}x(1 + {\sin ^2}x) + {\cos ^4}x(1 + {\cos ^2}x)\)\(\, + 5{\sin ^2}x{\cos ^2}x = 2.\)
Câu 3 (2,5 điểm). Cho phương trình
\({x^4} + 2(m – 2){x^2} + {m^2} – 5m + 5 = 0\)
1. Giải phương trình khi \(m = 1.\)
2. Tìm \(m\) để phương trình vô nghiệm.
Câu 4 (2 điểm).
1. Giải phương trình
\(2{x^2} – 6x – 1 = \sqrt {4x + 5} .\)
2. Giải hệ phương trình
\(\left\{ \begin{array}{l}12xy + 12({x^2} + {y^2}) + \dfrac{9}{{{{(x + y)}^2}}} = 85\\6x(x + y) + 3 = 13(x + y)\end{array} \right.\)
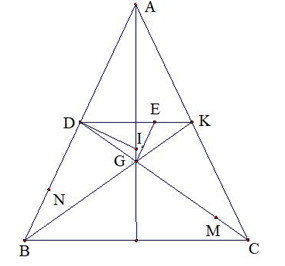
Câu 5 (1 điểm). Trong mặt phẳng tọa độ \(Oxy,\) cho tam giác \(ABC\) cân tại \(A,\) D là trung điểm của đoạn \(AB.\) Biết rằng \(I(\dfrac{{11}}{3};\dfrac{5}{3}),E(\dfrac{{13}}{3};\dfrac{5}{3})\) lần lượt là tâm đường tròn ngoại tiếp tam giác \(ABC,\)trọng tâm tam giác \(ADC;\) các điểm \(M(3; – 1),N( – 3;0)\) lần lượt thuộc các đường thẳng \(DC,AB.\) Tìm tọa độ đỉnh \(A,\) \(B,\) \(C\) biết \(A\) có tung độ dương.
Câu 6 (1 điểm). Cho tam giác \(ABC\) thỏa mãn
\(\dfrac{{a\cos A + b\cos B + c\cos C}}{{a\sin B + b\sin C + c\sin A}} \)\(\,= \dfrac{4}{9}(\dfrac{{a + b + c}}{{abc}})S\)
(Với S là diện tích của tam giác \(ABC,AB = c,AC = b,BC = a\)và A,B,C là các góc của tam giác ABC).
Chứng minh rằng tam giác \(ABC\) là tam giác đều.
Lời giải chi tiết
Câu 1:
ĐKXĐ: \(\left\{ \begin{array}{l}x – 2 \ne 0\\ – {x^2} + 5x – 4 \ge 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\1 \le x \le 4\end{array} \right.\)
\( \Leftrightarrow x \in \left[ {1;2} \right) \cup \left( {2;4} \right]\)
Tập xác định của hàm số đã cho là \(D = \left[ {1;2} \right) \cup \left( {2;4} \right].\)
Câu 2:
1. Tính giá trị của biểu thức
\(A = \cos \dfrac{{2\pi }}{5} + \cos \dfrac{{4\pi }}{5} + \cos \dfrac{{6\pi }}{5} + \cos \dfrac{{8\pi }}{5}.\)
Ta có:
\(\begin{array}{l}A = (\cos \dfrac{{2\pi }}{5} + \cos \dfrac{{8\pi }}{5}) + (\cos \dfrac{{4\pi }}{5} + \cos \dfrac{{6\pi }}{5})\\{\rm{ }} = 2\cos \pi \cos \dfrac{{3\pi }}{5} + 2\cos \pi \cos \dfrac{\pi }{5}\end{array}\)
\(\begin{array}{l} = – 2(\cos \dfrac{{3\pi }}{5} + \cos \dfrac{\pi }{5})\\ = – 4\cos \dfrac{{2\pi }}{5}\cos \dfrac{\pi }{5}\end{array}\)
\( = – 4\dfrac{{\sin \dfrac{\pi }{5}\cos \dfrac{\pi }{5}\cos \dfrac{{2\pi }}{5}}}{{\sin \dfrac{\pi }{5}}}\)
\( = – \dfrac{{\sin \dfrac{{4\pi }}{5}}}{{\sin \dfrac{\pi }{5}}}\) \( = – 1.\)
2. Chứng minh rằng
\({\sin ^4}x(1 + {\sin ^2}x) + {\cos ^4}x(1 + {\cos ^2}x) + 5{\sin ^2}x{\cos ^2}x = 2.\)
Ta có:
\(\begin{array}{l}{\rm{ }}{\sin ^4}x(1 + {\sin ^2}x) + {\cos ^4}x(1 + {\cos ^2}x) + 5{\sin ^2}x{\cos ^2}x\\ = ({\sin ^6}x + {\cos ^6}x) + {\sin ^4}x + {\cos ^4}x + 5{\sin ^2}x{\cos ^2}x\end{array}\)
\( = ({\sin ^2}x + {\cos ^2}x)({\sin ^4}x + {\cos ^4}x – {\sin ^2}x{\cos ^2}x) \)\(\,+ si{n^4}x + {\cos ^4}x + 5{\sin ^2}x{\cos ^2}x\)
\( = 2{\sin ^4}x + 2{\cos ^4}x + 4{\sin ^2}x{\cos ^2}x\)
\(\begin{array}{l} = 2{({\sin ^2}x + {\cos ^2}x)^2}\\ = 2.\end{array}\)
Câu 3: Cho phương trình
\({x^4} + 2(m – 2){x^2} + {m^2} – 5m + 5 = 0\)
1. Giải phương trình khi \(m = 1.\)
Khi \(m = 1\) ta được phương trình
\({x^4} – 2{x^2} + 1 = 0\)
\( \Leftrightarrow {x^2} = 1\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = – 1\end{array} \right.\)
KL: Vậy phương trình có hai nghiệm x = 1; x= -1
2. Tìm \(m\) để phương trình vô nghiệm.
Đặt \(t = {x^2}(t \ge 0).\) Ta được phương trình
\({t^2} + 2(m – 2)t + {m^2} – 5m + 5 = 0{\rm{ }}(1)\)
Để phương trình đã cho vô nghiệm thì phương trình (1) vô nghiệm hoặc phương trình (1) có hai nghiệm phân biệt đều âm hoặc phương trình (1) có nghiệm kép âm.
Để phương trình (1) vô nghiệm thì phải có
\({(m – 2)^2} – ({m^2} – 5m + 5) < 0 \)\(\,\Leftrightarrow m – 1 < 0 \Leftrightarrow m < 1\)
Để phương trình (1) có hai nghiệm đều âm thì ta phải có
\(\begin{array}{l}{\rm{ }}\left\{ \begin{array}{l}{(m – 2)^2} – ({m^2} – 5m + 5) > 0\\ – 2(m – 2) < 0\\{m^2} – 5m + 5 > 0\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}m \in (1; + \infty )\\m \in (2; + \infty )\\m \in ( – \infty ;\dfrac{{5 – \sqrt 5 }}{2}) \cup (\dfrac{{5 + \sqrt 5 }}{2}; + \infty )\end{array} \right.\\ \Leftrightarrow m \in (\dfrac{{5 + \sqrt 5 }}{2}; + \infty )\end{array}\)
Để phương trình (1) có nghiệm kép âm thì ta phải có
\(\left\{ \begin{array}{l}m – 1 = 0\\ – (m – 2) < 0\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}m = 1\\m > 2\end{array} \right.\)
Hệ phương trình này vô nghiệm.
Kết hợp lại ta được \(m \in ( – \infty ;1) \cup (\dfrac{{5 + \sqrt 5 }}{2}; + \infty )\) TMYCBT.
Câu 4:
1. Giải phương trình
\(2{x^2} – 6x – 1 = \sqrt {4x + 5} .\)
ĐKXĐ: \(x \ge – \dfrac{5}{4}{\rm{ }}(*)\)
Với điều kiện (*), ta có
\(2{x^2} – 6x – 1 = \sqrt {4x + 5} \)
\(\Leftrightarrow 4{x^2} – 12x – 2 = 2\sqrt {4x + 5} \)
\( \Leftrightarrow {(2x – 3)^2} = 2\sqrt {4x + 5} + 11\)
Đặt \(2y – 3 = \sqrt {4x + 5} \) (ĐK: \(y \ge \dfrac{3}{2})\)
Ta được hệ phương trình: \(\left\{ \begin{array}{l}{(2x – 3)^2} = 4y + 5{\rm{ }}(1)\\{(2y – 3)^2} = 4x + 5{\rm{ }}(2)\end{array} \right.\)
Trừ (1) cho (2) theo vế với vế ta được: \((x – y)(x + y – 2) = 0\)
\(\Leftrightarrow \left[ \begin{array}{l}x = y\\y = 2 – x\end{array} \right.\)
Với \(x = y\) ta được
\(\begin{array}{l}2x – 3 = \sqrt {4x + 5} \\ \Leftrightarrow \left\{ \begin{array}{l}2x – 3 \ge 0\\{(2x – 3)^2} = 4x + 5\end{array} \right.\\{\rm{ }}\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{3}{2}\\{x^2} – 4x + 1 = 0\end{array} \right.\\{\rm{ }} \Leftrightarrow x = 2 + \sqrt 3 \end{array}\)
Với \(y = 2 – x\) ta được \(1 – 2x = \sqrt {4x + 5} \)
\(\Leftrightarrow \left\{ \begin{array}{l}x \le \dfrac{1}{2}\\x = 1 \pm \sqrt 2 \end{array} \right. \)
\(\Leftrightarrow x = 1 – \sqrt 2 \)
KL: Vậy phương trình có nghiệm \(x = 1 – \sqrt 2 \) .
2. Giải hệ phương trình
\(\left\{ \begin{array}{l}12xy + 12({x^2} + {y^2}) + \dfrac{9}{{{{(x + y)}^2}}} = 85\\6x(x + y) + 3 = 13(x + y)\end{array} \right.\) (1)
ĐK: \(x + y \ne 0{\rm{ }}(*)\)
Với điều kiện (*), ta có:
\((1) \Leftrightarrow \left\{ \begin{array}{l}9{(x + y + \dfrac{1}{{x + y}})^2} + 3{(x – y)^2} = 103\\3(x + y + \dfrac{1}{{x + y}}) + 3(x – y) = 13\end{array} \right.{\rm{ }}(2)\)
Đặt \(\left\{ \begin{array}{l}a = x + y + \dfrac{1}{{x + y}}\\b = x – y\end{array} \right.\) (ĐK: \(\left| a \right| \ge 2{\rm{ }}(**))\)
Khi đó (2) trở thành: \(\left\{ \begin{array}{l}9{a^2} + 3{b^2} = 103\\3a + 3b = 13\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = \dfrac{{10}}{3}\\b = 1\end{array} \right.\\\left\{ \begin{array}{l}a = – \dfrac{7}{6}\\b = \dfrac{{11}}{2}\end{array} \right.\end{array} \right.\)
Kết hợp với ĐK (**) ta được: \(\left\{ \begin{array}{l}a = \dfrac{{10}}{3}\\b = 1\end{array} \right. \)
\(\Rightarrow \left\{ \begin{array}{l}x + y + \dfrac{1}{{x + y}} = \dfrac{{10}}{3}\\x – y = 1\end{array} \right.\)
Giải hệ trên ta được: \(\left\{ \begin{array}{l}x = \dfrac{2}{3}\\y = – \dfrac{1}{3}\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)
Kết hợp với ĐK (*) và KL: Vậy hệ phương trình đã cho có nghiệm: \(\left\{ \begin{array}{l}x = \dfrac{2}{3}\\y = – \dfrac{1}{3}\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)
Câu 5:

Gọi G là trọng tâm tam giác \(ABC\).Do \(ID \bot AB\) và \(EG\parallel AB\) nên \(ID \bot EG\), mà \(IG \bot DE\) nên I là trực tâm tam giác DEG\( \Rightarrow EI \bot DC \Rightarrow DC:x = 3\)
Gọi \(D(3;a)\). Ta có: \(\overrightarrow {DI} = (\dfrac{2}{3};\dfrac{{5 – 3a}}{3});\overrightarrow {DN} = ( – 6; – a)\)
Theo đề ra ta có: \(\overrightarrow {DI} .\overrightarrow {DN} = 0\) \( \Leftrightarrow – 4 – a\dfrac{{5 – 3a}}{3} = 0 \) \(\Leftrightarrow \left[ \begin{array}{l}a = 3\\a = – \dfrac{4}{3}\end{array} \right.\)
Với \(a = 3\) ta được \(D(3;3) \Rightarrow AB:x – 2y + 3 = 0;\) \(AI:x – y – 2 = 0\)
Tìm được \(A(7;5),B( – 1;1),C(3; – 3)\)
Với \(a = – \dfrac{4}{3}\) ta được \(D(3; – \dfrac{4}{3})\) \( \Rightarrow AB:2x + 9y + 6 = 0;\) \(AI:12x + 27y – 89 = 0\)
Tìm được \(A(\dfrac{{107}}{6}; – \dfrac{{125}}{{27}})\) (loại)
Câu 6:
\(\begin{array}{l}{\rm{ }}\dfrac{{a\cos A + b\cos B + c\cos C}}{{a\sin B + b\sin C + c\sin A}} = \dfrac{4}{9}(\dfrac{{a + b + c}}{{abc}})S\\ \Leftrightarrow \dfrac{{2{R^2}(\sin 2A + \sin 2B + \sin 2C)}}{{ab + bc + ca}} = \dfrac{{a + b + c}}{{9R}}\end{array}\)
\(\begin{array}{l} \Leftrightarrow \dfrac{{8{R^2}{\mathop{\rm sinAsinBsinC}\nolimits} }}{{ab + bc + ca}} = \dfrac{{a + b + c}}{{9R}}\\ \Leftrightarrow \dfrac{{abc}}{{R(ab + bc + ca)}} = \dfrac{{a + b + c}}{{9R}}\end{array}\)
\(\begin{array}{l} \Leftrightarrow (ab + bc + ca)(a + b + c) = 9abc\\ \Leftrightarrow a({b^2} – 2bc + {c^2}) + b({a^2} – 2ca + {c^2}) + c({a^2} – 2ab + {b^2}) = 0\end{array}\)
\(\begin{array}{l} \Leftrightarrow a{(b – c)^2} + b{(c – a)^2} + c{(a – b)^2} = 0\\ \Leftrightarrow \left\{ \begin{array}{l}b – c = 0\\c – a = 0\\a – b = 0\end{array} \right.\\ \Leftrightarrow a = b = c.\end{array}\)
Vậy tam giác ABC là tam giác đều.
