Chuyên đề Tam thức bậc hai – Toán 9

I. Phương pháp giải

• Bước 1 : Đặt điều kiện xác định của phương trình .
• Bước 2 : Đặt ẩn phụ đưa về phương trình bậc hai .
• Bước 3 : Biện luận tương quan số nghiệm giữa ẩn phụ với ẩn ban đầu trong phương trình sau khi biến đổi .Dùng công thức so sán nghiệm .
• Bước 4 : Kết luận nghiệm .

II.  Bài tập áp dụng

Câu 1 : 

Cho phương trình : $m^{2}+2(m+1)\sqrt{x}=x+5+4m$    (1)

Tìm m để phương trình có hai nghiệm phân biệt .

Hướng dẫn chi tiết :

$m^{2}+2(m+1)\sqrt{x}=x+5+4m$    (1)

Đk :  $x\geq 0$

Đặt  $t=\sqrt{x},(t\geq 0)$  , (1) <=> $m^{2}+2(m+1)t=t^{2}+5+4m$

<=>  $f(t)=t^{2}-2(m+1)t-m^{2}+4m+5=0$      (2)

Để (1)  có 2 nghiệm phân biệt => (2) phải có 2 nghiệm phân biệt không âm

<=>  $\left\{\begin{matrix}\Delta {}’ >0&  & \\ P\geq 0 &  & \\ S>0 &  & \end{matrix}\right.$ <=>  $\left\{\begin{matrix}(m+1)^{2}-(5+4m-m^{2})>0&  & \\ 5+4m-m^{2}\geq 0 &  & \\ 2(m+1) >0&  & \end{matrix}\right.$

<=>  $\left\{\begin{matrix}2m^{2}-2m-4>0&  & \\ 5+4m-m^{2}\geq 0 &  & \\ m+1 >0&  & \end{matrix}\right.$

<=>  $\left\{\begin{matrix}m<-1 // m>2&  & \\ -1\leq m\leq 5 &  & \\ m>-1&  & \end{matrix}\right.$

<=>  $2<m\leq 5$

Vậy để phương trình có hai nghiệm phân biệt  thì  $2<m\leq 5$ .

Câu 2 :

Cho phương trình : $2\sqrt{2x-x^{2}}-2m(\sqrt{x}+\sqrt{2-x})+2m^{2}-4=0$   (1)

Tim m để phương trình có bốn nghiệm phân biệt .

Hướng dẫn chi tiết :

         $2\sqrt{2x-x^{2}}-2m(\sqrt{x}+\sqrt{2-x})+2m^{2}-4=0$   (1)

Đk :  $0\leq x\leq 2$

Đặt  $t=\sqrt{x}+\sqrt{2-x}=> 2\sqrt{2x-x^{2}}=t^{2}-2$

Ta có : $t{}’=\frac{\sqrt{2-x}-\sqrt{x}}{2\sqrt{2x-x^{2}}}$

Để $t{}’=0<=>\frac{\sqrt{2-x}-\sqrt{x}}{2\sqrt{2x-x^{2}}}=0$

<=>  $\sqrt{2-x}=\sqrt{x}<=>  x =1$

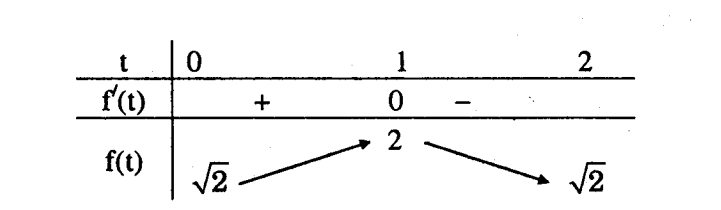
Bảng biến thiên :

=>   $\sqrt{2}\leq t\leq 2$

(1) <=>  $f(t)=t^{2}-2mt+2m^{2}-6=0$    (*)

Với  $\sqrt{2}\leq t\leq 2$   , thì pt $t=\sqrt{2}+\sqrt{2-x}$ có hai nghiệm x phân biệt .

Do đó , để (1) có bốn nghiệm phân biệt => (2) có hai nghiệm phân biệt $t_{1},t_{2}$ thỏa mãn :   $\sqrt{2}<t_{1}<t_{2}<2$

<=>  $\left\{\begin{matrix}\Delta {}’>0 &  &  & \\ f(\sqrt{2})>0 &  &  & \\ f(2)>0 &  &  & \\ \sqrt{2}<\frac{S}{2}<2 &  &  & \end{matrix}\right.$

<=>  $\left\{\begin{matrix}6-m^{2}>0 &  &  & \\ 2m^{2}-2\sqrt{2}m-4>0 &  &  & \\ 2m^{2}-4m-2>0 &  &  & \\ \sqrt{2}<m<2 &  &  & \end{matrix}\right.$

Nhận xét : Hệ trên vô nghiệm .

Vậy không có giá trị m nào thỏa mãn yêu cầu đề bài .

Câu 3 : 

Cho phương trình :  $2x\sqrt{4-x^{2}}-2(m-2)(x+\sqrt{4-x^{2}})+m^{2}=0$   (1)

Tìm m để phương trình có đúng hai nghiệm phân biệt .

Hướng dẫn chi tiết :

       $2x\sqrt{4-x^{2}}-2(m-2)(x+\sqrt{4-x^{2}})+m^{2}=0$   (1)

Đk :  $-2\leq x\leq 2$

Đặt   $t=x+\sqrt{4-x^{2}}=> 2x\sqrt{4-x^{2}}=t^{2}-4$

=>   $t{}’=1-\frac{x}{\sqrt{4-x^{2}}}=\frac{\sqrt{4-x^{2}}-x}{\sqrt{4-x^{2}}}$

Để  $t{}’=0<=>1-\frac{x}{\sqrt{4-x^{2}}}=\frac{\sqrt{4-x^{2}}-x}{\sqrt{4-x^{2}}}=0$

<=>  $\sqrt{4-x^{2}}=x=> x=\sqrt{2}$

Bảng biến thiên :

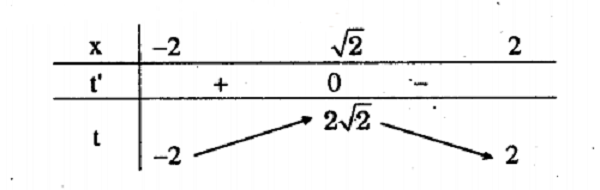
=>  $-2\leq t\leq 2\sqrt{2}$

(1) <=>  $f(t)=t^{2}-2(m-2)t+m^{2}-4=0$              (2)

+  Với $t=2\sqrt{2}$  hoặc $t\in [-2;2)$ , thì pt $t=x+\sqrt{4-x^{2}}$ có đúng một nghiệm x .

+  Với  $t\in [2;2\sqrt{2})$ , thì pt $t=x+\sqrt{4-x^{2}}$ có đúng hai nghiệm phân biệt x .

TH 1 : (2) có hai nghiệm $t_{1},t_{2}\in (-2;2)$

<=>  $\left\{\begin{matrix}\Delta {}’>0 &  &  & \\ f(-2)>0 &  &  & \\ f(2)>0 &  &  & \\ -2<\frac{S}{2}<2 &  &  & \end{matrix}\right.$   <=>  $2\sqrt{3}-2<m<2$

TH 2 : (2) có đúng 1 nghiệm $t\in (2;2\sqrt{2})$

+  Nếu là nghiệm kép $\in (2;2\sqrt{2})$  <=>  $\left\{\begin{matrix}\Delta{}’=0  & \\ t_{0}=m-2\in (2;2\sqrt{2}) & \end{matrix}\right.$

<=>  $\left\{\begin{matrix}m=2  & \\ m-2\in (2;2\sqrt{2}) & \end{matrix}\right.$

=>  Hệ vô nghiệm .

+  Nếu là hai nghiệm phân biệt  $t_{1},t_{2}$ thỏa mãn :  $\left\{\begin{matrix}2<t_{1}<2\sqrt{2}<t_{2} & \\ t_{1}<-2<2<t_{2}<2\sqrt{2} & \end{matrix}\right.$

Nhận xét : Hệ này vô nghiệm .

TH 3 : (2) có 1 nghiệm t = -2

<=>  $m^{2}+4m-8=0<=> m=-2-2\sqrt{3}\vee m=2\sqrt{3}-2$

+  Với $ m=-2-2\sqrt{3}$ , thì (2) <=> $t^{2}+2(4+2\sqrt{3})t+12+8\sqrt{3}=0$

<=>  Hoặc t = -2  ( t/mãn )  hoặc $t=-6-4\sqrt{3}$   ( loại )

+ Với $m=2\sqrt{3}-2$ , thì (2)  <=> $t^{2}-2(2\sqrt{3}-4)t+12-8\sqrt{3}=0$

<=>  Hoặc t = -2  hoặc  $t=4\sqrt{3}-6$    ( t/mãn )

=>  $m=2\sqrt{3}-2$   thỏa mãn yêu cầu đề bài .

TH 4 : (2) có 1 nghiệm t = 2

=>  $m^{2}-4m+8=0$    ( vô nghiệm )

TH 5 : (2) có 1 nghiệm $t=2\sqrt{2}$

=>  $m^{2}-4\sqrt{2}m+4+8\sqrt{2}=0$   ( vô nghiệm )

Vậy các giá trị thỏa mãn là $2\sqrt{3}-2\leq m<2$ .