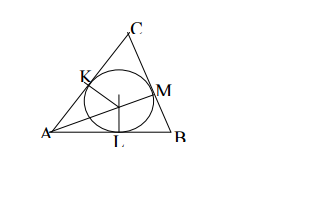
A. Tổng quan kiến thức
1. Đa giác lồi.
2. Đa giác đều.
3. Tổng các góc trong đa giác n cạnh là : $(n – 2). 180^{\circ}$.
4. Số đường chéo của một đa giác n cạnh là : $\frac{(n-3)n}{2}$.
5. Tổng các góc ngoài của một đa giác n cạnh là : $360^{\circ}$.
6. Trong một đa giác đều, giao điểm O của hai đường phân giác của hai góc là tâm của đa giác đều.
Tâm O cách đều các đỉnh, cách đều các cạnh của đa giác đều, có một đường tròn tâm O đi qua các đỉnh của đa giác đều gọi là đường tròn ngoại tiếp đa giác đều.
7. Diện tích tam giác: $\frac{1}{2}a.h$ (a: cạnh đáy; h: chiều cao tương ứng) .
$S=\frac{1}{2}a.b.\sin C $ ( a = AB; b = CA )
8. Diện tích hình chữ nhật : S = a.b
9. Diện tích hình vuông : S = $a^{2}$
10. Diện tích hình bình hành : S = a.h (h là chiều cao kẻ từ một đỉnh đến cạnh a)
11. Diện tích hình thoi : $ S=\frac{1}{2}AC.BD$ (AC; BD là hai đƣờng chéo)
12. Diện tích hình thang $ S=\frac{1}{2}(AB+CD).AH$ (AB, CD là hai đáy; AH: chiều cao)
13. Một số kết quả cần nhớ :
a) $S_{ABM} = S_{ACM }$ ( AM là trung tuyến tam giác ABC)
b) AA‟ // BC => $S_{ABC} = S_{A‟BC}$
c) $\frac{S_{ABD}}{S_{DBC}}=\frac{BD}{CD}$ (D thuộc BC của tam giác ABC)
d) $\frac{S_{ABD}}{S_{DBC}}=\frac{AH}{DK}$ (AH; DK là đƣờng cao của tam giác ABC và DBC)
e) $\frac{S_{AMN}}{S_{ABC}}=\frac{AM}{AB}.\frac{AN}{AC}$ (M thuộc BC; N thuộc AC của tam giác ABC)
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Bài 1: Cho hình thang ABCD, đáy AB = 3cm, AD = 4cm, BC = 6cm, CD = 9cm. Tính diện tích hình thang .
Vẽ BE AD // ta có:$S=\frac{3+9}{2}h=6h$ ($cm^{2}$) .
Xét $\triangle CBE$ cân ở C , ta có :
$IC^{2}=36-4=32 => IC=4\sqrt{2} (cm)$
$S_{BCE}=\frac{4.4\sqrt{2}}{2}=8\sqrt{2}$ ($cm^{2}$) .
=> h = BK = $\frac{8\sqrt{5}.2}{6}=\frac{8\sqrt{2}}{3}$
=> $S_{ABCD}=6h=6.\frac{8\sqrt{2}}{3}=16\sqrt{2} (cm^{2})$
Vậy $S_{ABCD}=16\sqrt{2} (cm^{2})$ .
Bài 2: Cho $\triangle ABC$ có chu vi là 2p, cạnh BC = a, gọi góc $\widehat{BAC}=\alpha $ , đường tròn nội tiếp tam giác ABC tiếp xúc cạnh AC tại K.
Tính diện tích $\triangle AOK$ .
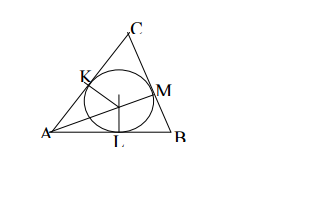
Ta có : AK = AL; CK = CM; BM = BL
=> 2 CM + 2 AK + 2 BM = 2p .
Mà AK = p – (BM + CM) <=> AK = p – a
Vì theo giả thiết : $\widehat{BAC}=\alpha $
=> $\widehat{KAO}=\frac{\alpha }{2}$
+ OK = (p – a)$\tan \frac{\alpha }{2}$
=> $S_{AOK}=\frac{1}{2}AK.AO=\frac{1}{2}(p-a)^{2}\tan \frac{\alpha }{2}$ .
Bài 3: Cho $\triangle ABC$ . Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho $\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{3}$ . Gọi O là giao điểm của BN và CM.
Gọi H, L lần lượt là chân đường vuông góc kẻ từ A, C tới đường thẳng BN.
a/ Chứng minh CL = 2 AH.
b/ Chứng minh: $S_{BOC} = 2S_{BOA}$ .
Kẻ CE và BD vuông góc với AO. Chứng minh BD = CE.
c/ Giả sử $S_{ABC} = 20 cm^{2}$ , tính $S_{AMON}$ .
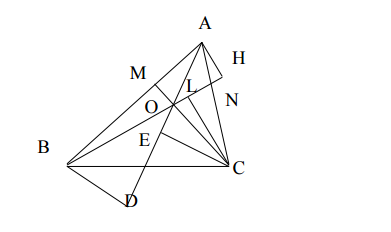
a/ Ta có : CN = 2 AN => $S_{BNC}=2S_{BNA}$ (1)
BN là cạnh chung (2)
Từ (1) ,(2) => $S_{BNC}=2S_{BNA}$
Ta có : $S_{BOC}=\frac{1}{2}BO.CL$
$S_{BOA}=\frac{1}{2}BO.AH$.
Và CL = 2AH . (đpcm).
b/ Từ câu (a) => $S_{BOC}=2S_{BOA}$ . (*)
Tương tự , ta có : $S_{BOC}=2S_{COA}$ (**)
Từ (*), (**) => $S_{BOA}=2S_{COA}$ (đpcm)
Kẻ $CE\perp AO,BD\perp CE => BD=CE$ . (đpcm)
c/ Giả sử $S_{BOC}=2a (cm^{2})$ => $S_{BOA}=a (cm^{2})$
$S_{COA}=a (cm^{2})$
=> $S_{ABC}=4a (cm^{2})$
Mà theo giả thiết : $S_{ABC}=20 (cm^{2})$
=> a = 5 (cm)
Mặt khác , ta có : $S_{ONA}=S_{OMA}=\frac{1}{3} a=\frac{5}{3} (cm^{2})$
=> $S_{OAMN}=2S_{OMA}=\frac{10}{3} (cm^{2})$ .
Bài 4: Cho hình thang ABCD, đáy AB, O là giao điểm của hai đường chéo AC và BD.
a. Chứng minh rằng: $S_{OAD}=S_{OBC}$ .
b. $S_{OAB}.S_{OCD}=(S_{OBC})^{2}$ .
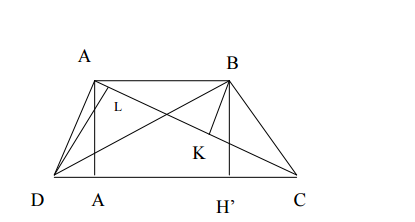
a/ Kẻ đường cao AH và $BH{}’$ => AH = BH‟
Ta có: $S_{ADC}=\frac{1}{2}AH.DC$
$S_{BDC}=\frac{1}{2}BH{}’.DC$
=> $S_{ADC}=S_{BDC} =>S_{ODA}=S_{OBC}$ .
b/ Kẻ đường cao BK của $\triangle ABC$ ta có:
$\frac{S_{OAB}}{S_{OBC}}=\frac{OA}{OC}$ (1)
Tương tự , ta có : $\frac{S_{OAD}}{S_{OCD}}=\frac{OA}{OC}$ (2)
Mà theo câu (a) : $S_{ODA}=S_{OBC}$
Từ (1) ,(2) => $\frac{S_{OAD}}{S_{OCD}}=\frac{S_{OAB}}{S_{OBC}}$ (đpcm)
Bài 5: Cho $\triangle ABC$ biết : $\widehat{A}=\alpha ,\widehat{B}=\beta ,\widehat{C}=\delta $, đường tròn nội tiếp tam giác có bán kính bằng r. P, Q, R là các tiếp điểm. Tính diện tích tam giác PQR .
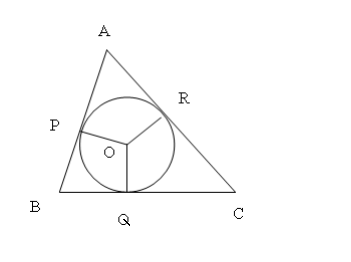
Từ hình vẽ ta có : OP = OQ = OR = r.
=> $S_{PQR} = S_{OPR} + S_{OPQ} + S_{OQR}$
Cụ thể : $S_{OPR} =\frac{1}{2}r^{2}\sin (180^{\circ}-\alpha )=\frac{1}{2}r^{2}\sin \alpha $ (1)
$S_{OPQ} =\frac{1}{2}r^{2}\sin (180^{\circ}-\beta )=\frac{1}{2}r^{2}\sin \beta $ (2)
$S_{OQR} =\frac{1}{2}r^{2}\sin (180^{\circ}- \delta )=\ frac{1}{2}r^{2}\sin \delta $ (3)
Từ (1), (2) ,(3) => $S_{PQR} = \frac{1}{2}r^{2}(\sin \alpha +\sin \beta +\sin \delta )$ (đpcm).
