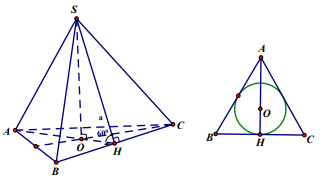
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa mặt bên và đáy bằng , diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp tam giác ABC là: 

Tam giác ABC đều nên tâm O đừng tròn nội tiếp là trọng tâm của tam giác ABC \(\Rightarrow \mathrm{R}=\mathrm{OH}=\frac{1}{3} \mathrm{AH}=\frac{1}{3} \cdot \frac{\mathrm{a} \sqrt{3}}{2}=\frac{\mathrm{a} \sqrt{3}}{6}\).

Ta có:

\(\left\{ \begin{array}{l}
SH \bot BC\\
AH \bot BC\\
BC = \left( {SBC} \right) \cap \left( {ABC} \right)
\end{array} \right. \Rightarrow \widehat {\left( {SBC} \right),\left( {ABC} \right)} = \widehat {SHA}\)

Khi đó:

\(1=\mathrm{SH}=\frac{\mathrm{OH}}{\cos 60^{0}}=\frac{\frac{\mathrm{a}}{2 \sqrt{3}}}{\frac{1}{2}}=\frac{\mathrm{a}}{\sqrt{3}}\)

\(\text { Vậy } \mathrm{S}_{\mathrm{xq}}=\pi \frac{\mathrm{a} \sqrt{3}}{6} \cdot \frac{\mathrm{a}}{\sqrt{3}}=\frac{\pi \mathrm{a}^{2}}{6}\)