|
ĐỀ ÔN THI GIỮA HK1 MÔN: TOÁN NĂM HỌC : 2021 – 2022 |
Đề 1
Phần I.Trắc nghiệm
Câu 1.Căn bậc hai số học của 9 là
| A. -3. | B. 3. | C. 81. | D. -81. |
Câu 2.Biểu thức \(\sqrt {1 – 2x} \) xác định khi:
| A. \(x > \frac{1}{2}\) | B. \(x \ge \frac{1}{2}\) | C. \(x < \frac{1}{2}\) | D. \(x \le \frac{1}{2}\) |
Câu 3: Hàm số y =(2m+6)x + 5 là hàm số bậc nhất khi
A. x > -3 ; B. m \(\ne \) 3; C. m \(\ne \) – 3; D. x < 3.
Câu 4: Hàm số y =(-m+3)x -15 là hàm số đồng biến khi
A. m > -3 ; B. m \(\ne \) 3; C. m \(\ge \) 3; D. m < 3
Câu 5.Biểu thức \(\sqrt {{{\left( {3 – 2x} \right)}^2}}\) bằng
| A. 3 – 2x. | B. 2x – 3. | C. \(\left| {2x – 3} \right|\) | D. 3 – 2x và 2x – 3. |
Câu 6.Giá trị của biểu thức \(c{\rm{o}}{{\rm{s}}^{\rm{2}}}{20^0} + c{\rm{o}}{{\rm{s}}^{\rm{2}}}{40^0} + c{\rm{o}}{{\rm{s}}^{\rm{2}}}{50^0} + c{\rm{o}}{{\rm{s}}^{\rm{2}}}{70^0}\) bằng
| A. 1. | B. 2. | C. 3. | D. 0. |
Câu 7.Giá trị của biểu thức \(\frac{1}{{2 + \sqrt 3 }} + \frac{1}{{2 – \sqrt 3 }}\) bằng
| A. \(\frac{1}{2}\) | B. 1. | C. -4. | D. 4. |
Câu 8.Cho tam giác ABC vuông tại A có AB = 18; AC = 24. Bán kính đường tròn ngoại tiếp tam giác đó bằng
| A. 30. | B. 20. | C. 15. | D. 15 . |
Câu 9.Trong các hàm số sau, hàm số nào là hàm số bậc nhất ?
| A. \(y = \sqrt {\frac{x}{2}} + 4\) | B. \(y = \frac{{\sqrt 2 x}}{2} – 3\) | C. \(y = \frac{{ – 2}}{x} + 1\) | D. \(y = – \frac{{3\sqrt x }}{5} + 2\) |
Câu 10.Trong các hàm số sau, hàm số nào đồng biến ?
A. y = 2 – x B. \(y = – \frac{1}{2}x + 1\) C. \(y = \sqrt 3 – \sqrt 2 \left( {1 – x} \right)\) D. y = 6 – 3(x – 1).
Câu 11.Điểm nào trong các điểm sau thuộc đồ thị hàm số y = 1 – 2x ?
| A. (-2; -3). | B. (-2; 5). | C. (0; 0). | D. (2; 5). |
Câu 12.Nếu hai đường thẳng y = -3x + 4 (d1) và y = (m+1)x + m (d2) song song với nhau thì m bằng
| A. – 2. | B. 3. | C. – 4. | D. – 3. |
Phần II. Tự luận
Câu 1: Cho biểu thức: P = \(\left( {\frac{{x\sqrt x – 1}}{{x – \sqrt x }} – \frac{{x\sqrt x + 1}}{{x + \sqrt x }}} \right):\left[ {\frac{{2(x – 2\sqrt x + 1)}}{{x – 1}}} \right]\)
Rút gọn P
Câu 2: Cho nửa đường tròn (O) đường kính AB. Vẽ các tiếp tuyến Ax, By về nửa mặt phẳng bờ AB chứa nửa đường tròn. Trên Ax và By theo thứ tự lấy M và N sao cho góc MON bằng 900
Gọi I là trung điểm của MN. Chứng minh rằng:
a) AB là tiếp tuyến của đường tròn (I;IO)
b) MO là tia phân giác của góc AMN
c) MN là tiếp tuyến của đường tròn đường kính AB
ĐÁP ÁN
Phần I. Trắc nghiệm
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | D | C | D | C | B | D | C | B | C | B | C |
Phần II. Tự luận
Câu 1:
a)
– ĐKXĐ: \(0 \le x \ne 1\)
– Rút gọn
P = \(\left( {\frac{{{{\sqrt x }^3} – {1^3}}}{{\sqrt x (\sqrt[{}]{x} – 1\left. {} \right)}} – \frac{{{{\sqrt x }^3} + {1^3}}}{{\sqrt x (\sqrt x + 1)}}} \right):\left( {\frac{{2.{{(\sqrt x – 1)}^2}}}{{{{\sqrt x }^2} – {1^2}}}} \right)\)
\( \Leftrightarrow P = \left( {\frac{{(\sqrt x – 1)(x + \sqrt x + 1)}}{{\sqrt x (\sqrt x – 1)}} – \frac{{(\sqrt x + 1)(x – \sqrt x + 1)}}{{\sqrt x (\sqrt x + 1)}}} \right):\left( {\frac{{2{{(\sqrt x – 1)}^2}}}{{(\sqrt x – 1)(\sqrt x + 1)}}} \right)\)
\( \Leftrightarrow P = \left( {\frac{{x + \sqrt x + 1}}{{\sqrt x }} – \frac{{x – \sqrt x + 1}}{{\sqrt x }}} \right):\left( {\frac{{2(\sqrt x – 1)}}{{\sqrt x + 1}}} \right)\)
\(\Leftrightarrow P = \left( {\frac{{x + \sqrt x + 1 – x + \sqrt x – 1}}{{\sqrt x }}} \right).\left( {\frac{{\sqrt x + 1}}{{2(\sqrt x – 1)}}} \right)\)
\( \Leftrightarrow P = \left( {\frac{{2\sqrt x }}{{\sqrt x }}} \right).\left( {\frac{{\sqrt x + 1}}{{2(\sqrt x – 1)}}} \right)\)
\( \Leftrightarrow P = \frac{{\sqrt x + 1}}{{\sqrt x – 1}}\)
……….
Đề 2
Phần I. Trắc nghiệm
Câu 1: \(\sqrt {21 – 7x}\)có nghĩa khi
A. x \(\ge \)- 3;
B. x \(\le \) 3 ;
C. x > -3 ;
D. x <3.
Câu 2: Rút gọn biểu thức \(\sqrt {(5 – \sqrt {13} ){}^2} \) được
A. 5 – \(\sqrt {13}\)
B. -5 – \(\sqrt {13}\)
C. \(\sqrt {13}\)- 5
D. \(\sqrt {13}\) + 5.
Câu 3: Rút gọn các biểu thức \(3\sqrt {3a} + 4\sqrt {12a} – 5\sqrt {27a}\) (a \(\ge \) 0) được
A. \(4\sqrt {3a}\)
B. \(26\sqrt {3a}\)
C. \(-26\sqrt {3a}\)
D. \(-4\sqrt {3a}\)
Câu 4: Giá trị biểu thức \(\sqrt {16} \cdot \sqrt {25} + \frac{{\sqrt {196} }}{{\sqrt {49} }}\) bằng
A. 28
B. 22
C.18
D. \(\sqrt 2\)
Câu 5: Tìm x biết \(\sqrt[3]{x} = – 1,5\). Kết quả
A. x = -1,5
B. -3,375
C. 3,375
D. -2,25
Câu 6: Rút gọn biểu thức \(\sqrt[3]{27{{x}^{3}}}-\sqrt[3]{8{{x}^{3}}}+4x\) được
A. 23\(\sqrt[3]{x}\)
B. 23x
C. 15x
D. 5x
Câu 7: Rút gọn biểu thức \(\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}\) (điều kiện \(4\le x<8\)) bằng
A. \(2\sqrt{x-4}\)
B. – 4
C. \(2\sqrt{x+4}\)
D. 4
Câu 8: Khử mẫu của biểu thức \(\sqrt{\frac{2}{5{{a}^{3}}}}\) với a>0 được
A. \(\frac{\sqrt{10a}}{5{{a}^{2}}}\)
B. \(\frac{\sqrt{10a}}{5{{a}^{3}}}\)
C. \(\frac{\sqrt{2}}{5{{a}^{2}}}\)
D. \(\frac{2}{5{{a}^{2}}}\)
Câu 9: Rút gọn biểu thức \(\frac{2}{\sqrt{7}-3}-\frac{2}{\sqrt{7}+3}\) được
A. \(\sqrt{7}+3\)
B. \(\sqrt{7}-3\)
C.-6
D. 0
Câu 10: \(\sqrt{9{{x}^{2}}}=12\)
A. x = \(\pm 2\)
B. \(\pm 4\)
C. 2
D. -2
……….
Đề 3
Câu 1. Rút gọn các biểu thức
a) A = \(5\sqrt 3 + \sqrt {27} – 3\sqrt {\frac{1}{3}} \)
b) B = \(\sqrt {{{\left( {\sqrt 3 – 1} \right)}^2}} – \sqrt {4 + 2\sqrt 3 } \)
c) C = \(\frac{{\sqrt {{y^3}} – 1}}{{y + \sqrt y + 1}} – \frac{{y + 3\sqrt y + 2}}{{\sqrt y + 1}}\) (với y \( \ge\) 0).
Câu 2. Cho hàm số y = (m – 1) x +3 (với m là tham số).
a) Xác định m biết M(1; 4) thuộc đồ thị của hàm số trên.
b) Vẽ đồ thị của hàm số trên với m = 2.
Câu 3. Tìm x biết:
a) \(\sqrt{{{x}^{2}}+4x+4}=1\);
b) \(\sqrt{7+\sqrt{2+\sqrt{x+1}}}=3\).
ĐÁP ÁN
Câu 1:
a) A = \(5\sqrt{3}+\sqrt{27}-3\sqrt{\frac{1}{3}}\)
A = \(5\sqrt{3}+\sqrt{9.3}-\sqrt{{{3}^{2}}.\frac{1}{3}}=5\sqrt{3}+3\sqrt{3}-\sqrt{3}\)
A =\(7\sqrt{3}\)
b) B = \(\sqrt{{{\left( \sqrt{3}-1 \right)}^{2}}}-\sqrt{4+2\sqrt{3}}\)
\(\sqrt{{{\left( \sqrt{3}-1 \right)}^{2}}}=\left| \sqrt{3}-1 \right|=\sqrt{3}-1\) vì \(\sqrt{3}>1\)
\(\sqrt{4+2\sqrt{3}}=\sqrt{3+2\sqrt{3}+1}=\sqrt{{{\left( \sqrt{3}+1 \right)}^{2}}}=\left| \sqrt{3}+1 \right|=\sqrt{3}+1\)
Do đó B = \(\sqrt{3}-1-\left( \sqrt{3}+1 \right)=\sqrt{3}-1-\sqrt{3}-1=-2\)
c) C = \(\frac{\sqrt{{{y}^{3}}}-1}{y+\sqrt{y}+1}-\frac{y+3\sqrt{y}+2}{\sqrt{y}+1}\) (với y \(\ge \) 0)
Phân tích các tử về dạng tích:
\(\sqrt{{{y}^{3}}}-1=\left( \sqrt{y}-1 \right)\left( y+\sqrt{y}+1 \right)\)
\(y+3\sqrt{y}+2=\left( y+\sqrt{y} \right)+\left( 2\sqrt{y}+2 \right)=\left( \sqrt{y}+1 \right)\left( \sqrt{y}+2 \right)\)
C = \(\frac{\left( \sqrt{y}-1 \right)\left( y+\sqrt{y}+1 \right)}{y+\sqrt{y}+1}-\frac{\left( \sqrt{y}+1 \right)\left( \sqrt{y}+2 \right)}{\sqrt{y}+1}\)=\(\sqrt{y}-1-\left( \sqrt{y}+2 \right)=-3\)
……….
Đề 4
Phần I. Trắc nghiệm
Câu 1: Biểu thức \(\sqrt {2x – 1}\)xác định khi:
A. \(x \le \frac{1}{2}\)
B. \(x \ge \frac{1}{2}\)
C. \(x < \frac{1}{2}\)
D. \(x > \frac{1}{2}\)
Câu 2: Hàm số \(y = – 2x + 1\) có đồ thị là hình nào sau đây?
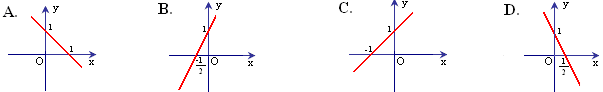
Câu 3: Giá trị của biểu thức \(\frac{1}{{2 + \sqrt 3 }} + \frac{1}{{2 – \sqrt 3 }}\) bằng
A. \(\frac{1}{2}\)
B. 1
C. 4
D. – 4
Câu 4: Đường tròn là hình:
A. Không có trục đối xứng
B. Có một trục đối xứng
C. Có hai trục đối xứng
D. Có vô số trục đối xứng
Câu 5: Trong các hàm số sau, hàm số nào đồng biến ?
| A. y = 2 – x. | B. y=-5x+1. | C. \(y=(\sqrt{3}-1)x-\sqrt{2}\). | D. y = 6 – 3(x – 1) |
Câu 6: Nếu hai đường thẳng y = -3x + 4 (d1) và y = (m+1)x + m (d2) song song với nhau thì m bằng
| A. – 2. | B. -4 | C. 4. | D. – 3. |
Câu 7: Trên hình 1.2 ta có:
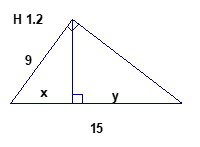
A. x = 5,4 và y = 9,6
B. x = 5 và y = 10
C. x = 10 và y = 5
D. x = 9,6 và y = 5,4
Câu 8: Cho tam giác ABC vuông tại A có AB = 18; AC = 24. Bán kính đường tròn ngoại tiếp tam giác đó bằng
| A. 30. | B. 20. | C. 15. | D. 15\(\sqrt{2}\). |
Câu 9: Cho (O; 1 cm) và dây AB = 1 cm. Khoảng cách từ tâm O đến AB bằng
| A. \(\frac{1}{2}\) cm. | B. \(\frac{\sqrt{3}}{2}\) cm. | C. \(\frac{\sqrt{3}}{3}\) cm. | D. \(\frac{1}{\sqrt{3}}\) cm. |
Câu 10: Cho \(\alpha ={{35}^{O}};\beta ={{55}^{O}}\). Khi đó khẳng định nào sau đây là Sai?
| A. sin\(\alpha \) = sin\(\beta \) | B. sin\(\alpha \) = cos\(\beta \) | C. tan\(\alpha \) = cot\(\beta \) | D. cos\(\alpha \) = sin\(\beta \) |
