Bài 13 trang 134 SBT Toán 8 tập 2
Khi gấp và dán hình dưới đây (h.107), hình nào tạo thành hình lập phương ? Hãy điền “có”, “không” vào chỗ trống (…).
(hình 107 trang 134 sbt)
Trả lời:
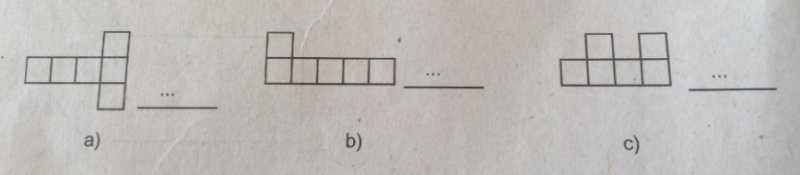
a. Có
b. Không
c. Không
Bài 14 trang 135
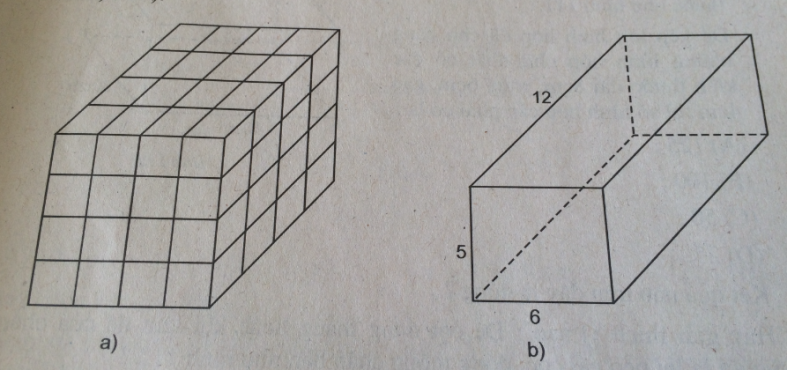
Tìm số hình lập phương đơn vị (hình lập phương có cạnh là 1) ở các hình 108a và b.
Giải: (hình 108 trang 135 sbt)
Hình 14a:
Số hình lập phương đơn vị là: 4 × 4 × 4 = 64 (hình)
Hình 14b:
Số hình lập phương đơn vị là: 5 × 6 × 12 = 360 (hình)
Bài 15
Từ một đoạn dây thép ngắn hơn 1,5m, liệu người ta có thể tạo ra một cái khung hình lập phương có cạnh là 1dm được hay không ? (đoạn dây thép để nguyên, không cắt)
Giải: Mỗi hình lập phương có 12 cạnh, mỗi cạnh là 1dm. Vậy cần ít nhất 12dm hay 1,2m để tạo ra hình lập phương có cạnh là 1dm.
Vậy có thể tạo ra một hình lập phương có cạnh là 1dm được nếu đoạn dây đó dài 1,2m
Bài 16 trang 135
Quan sát hình hộp chữ nhật (h.109) và trả lời các câu hỏi sau:
a. Ba đường thẳng nào cắt nhau tại điểm G ?
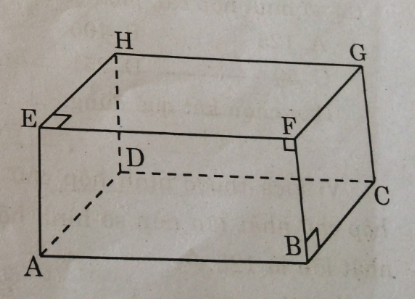
b. Hai mặt phẳng nào cắt nhau theo đường thẳng FB ?
c. Mặt phẳng (EFBA) và mặt phẳng (FGCB) cắt nhau theo đường thẳng nào ?
HD giải: (hình 109 trang 135 sbt)
a. Ba đường thẳng CG, HG, FG cắt nhau tại G.
b. Mặt phẳng (ABFE) và mặt phẳng (BCGF) cắt nhau theo đường thẳng BF.
c. Mặt phẳng (EFBA) và mặt phẳng (FGCB) cắt nhau theo đường thẳng BF.
Bài 17 trang 135
Cạnh của hình lập phương bằng \(\sqrt 2 \) (h.110).
Như vậy độ dài đoạn AC1 là :
A. 2
B. \(2\sqrt 6 \)
C. \(\sqrt 6 \)
D. \(2\sqrt 2 \)
Kết quả nào trên đây là đúng ?
HD giải: (hình 110 trang 135 sbt)
Áp dụng định lí Pi-ta-go, ta tính được:
– Đường chéo mặt đáy bằng: \(\sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}} = 2\)
– Đường chéo của mặt chéo:
Ta có: \(A{C_1}^2 = {2^2} + {\left( {\sqrt 2 } \right)^2} = 4 + 2 = 6\)
Suy ra: \(A{C_1} = \sqrt 6 \)
Vậy chọn đáp án C.
Bài 18 trang 136
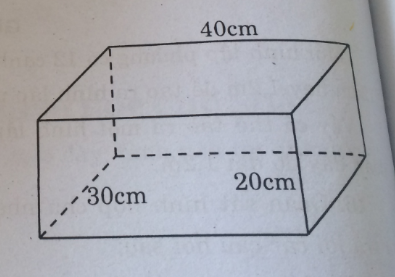
Một hình hộp chữ nhật có kích thước như hình 111.
Để xếp kín hình hộp đã cho bằng những hình hộp chữ nhật có các kích thước dài 8cm, rộng 6cm, cao 4cm thì số hình hộp cần phải có là :
A. 125
B. 100
C. 50
D. 25
Kết quả nào trên đây là đúng ?
HD giải: (hình 111 trang 136 sbt)
Vì kích thước hình hộp chữ nhật nhỏ là ước của kích thước hình hộp chữ nhật lớn nên số hình hộp chữ nhật nhỏ xếp kín hình hộp chữ nhật lớn là 125.
Vậy chọn đáp án A
Bài 19 trang 136 SBT Toán 8 tập 2
Hãy giải thích vì sao: Để cột đứng thẳng hoặc khi làm đế của chân bàn, người ta lại néo cái cọc, đóng rộng chân bàn như hình 112 ?
Bài giải: (hình 112 trang 136 sbt)
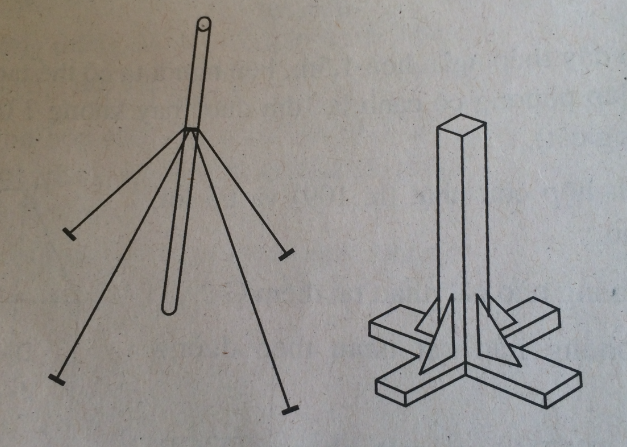
Vì cái cọc hay chân bàn đều vuông góc với mặt phẳng là mặt đất nên đê cái cọc hay chân bàn đứng vững người ta dùng ít nhất là 3 điểm không thẳng hàng trên mặt đất để định vị.
Bài 20 trang 136 Sách bài tập Toán 8 tập 2
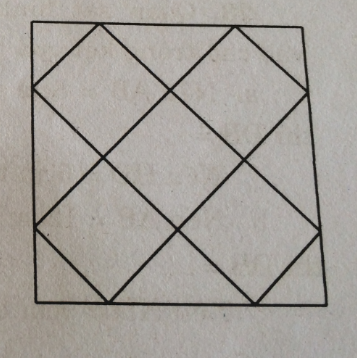
Từ một tờ giấy hình vuông kích thước 3 × 3 liệu có thể gấp để tạo thành một hình lập phương đơn vị hay không ?
(có thể làm nắp rời)
Giải: (hình trang 133 sgbt)
Triển khai hình lập phương không có nắp ta được 1 hình chữ thập gồm 2 hình chữ nhật có chiều rộng 1 ( đơn vị dài ) và chiều dài 3 ( đơn vị dài )
Sắp xếp như hình vẽ, ta có tam giác vuông cân ở góc nhỏ có cạnh huyền 1 đơn vị dài thì cạnh góc vuông là \({{\sqrt 2 } \over 2}\) ( đơn vị dài )
Tam giác vuông cân có cạnh huyền là 3 đơn vị dài thì cạnh góc vuông bằng \({{3\sqrt 2 } \over 2}\) đơn vị dài.
Khi đó tổng độ dài là \({{3\sqrt 2 } \over 2} + {{\sqrt 2 } \over 2} = 2\sqrt 2 \) đơn vị dài < 3
Vậy hình chữ thập đó đặt gọn trong tờ giấy có kích thước 3×3
Phần thừa ở 4 góc là 4 tam giác vuông đủ để làm nắp
Vậy có thể gấp được hình lập phương đơn vị từ tờ giấy 3×3
Bài 21 trang 136
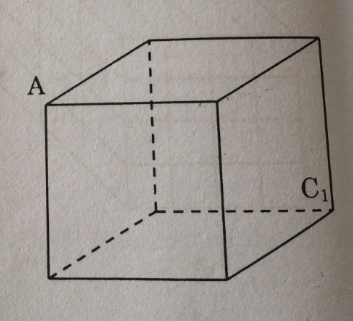
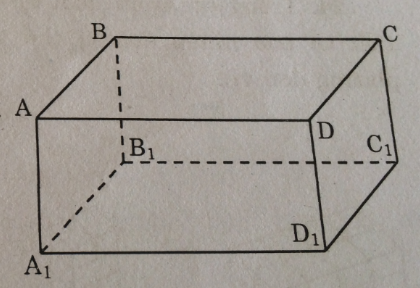
Tìm trên hình hộp chữ nhật ABCD.A1B1C1D1 (h.113) một ví dụ cụ thể để chứng tỏ mệnh đề sau là sai:
Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
HD giải: (hình 113 trang 136 sbt)
Ta có: AB ⊥ BC
CC1 ⊥ BC
Nhưng AB và CC1 không song song với nhau.
Vậy mệnh đề đã cho là sai
Bài 22 trang 137
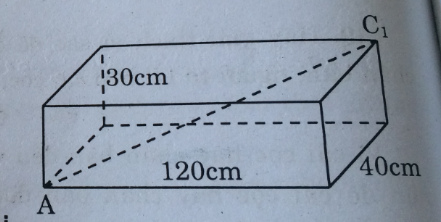
Các kích thước của một hình hộp chữ nhật như ở hình 114, độ dài đoạn AC1 là:
A. 190cm
B. 150cm
C. 130cm
D. 109cm
Hãy chọn kết quả đúng.
Giải:
Áp dụng định lí Pi-ta-go, ta tính được:
– Đường chéo của mặt đáy bình phương bằng: \({40^2} + {120^2}\)
– Đường chéo của mặt chéo bình phương bằng: \({40^2} + {120^2} + {30^2}\)
Suy ra: \(A{C_1} = \sqrt {{{40}^2} + {{120}^2} + {{30}^2}} = 130\)
Vậy chọn đáp án C
Bài 23 trang 137
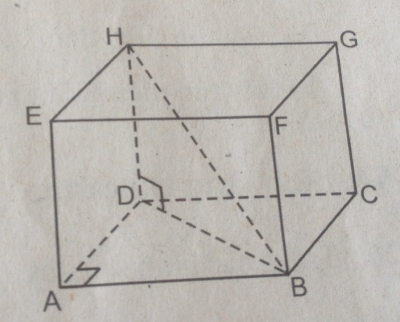
Quan sát hình 115 và điền vào chỗ trống (…) kết quả bằng số:
a. Nếu AB = 8cm và AD = 6cm thì DB = … và nếu HD = 5cm thì HB = …
b. Nếu AB = 12cm và AD = 8cm thì DB = … và nếu HD = 9cm thì HB = …
Giải:
Áp dụng định lí Pi-ta-go, tính được:
a. Nếu AB = 8cm và AD = 6cm thì DB = 10cm
Nếu HD = 5cm thì HB = \(\sqrt {125} \) cm
b. Nếu AB = 12cm và AD = 8cm thì DB= \(\sqrt {208} \) cm
Nếu HD = 9cm thì HB = 17cm
Bài 24 trang 137
Trong các hình dưới đây (h.116), mỗi hình gồm bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích ( mỗi hình nhỏ là một hình lập phương đơn vị).
Giải: Hình a có kích thước là 4; 2 và 2 đơn vị dài
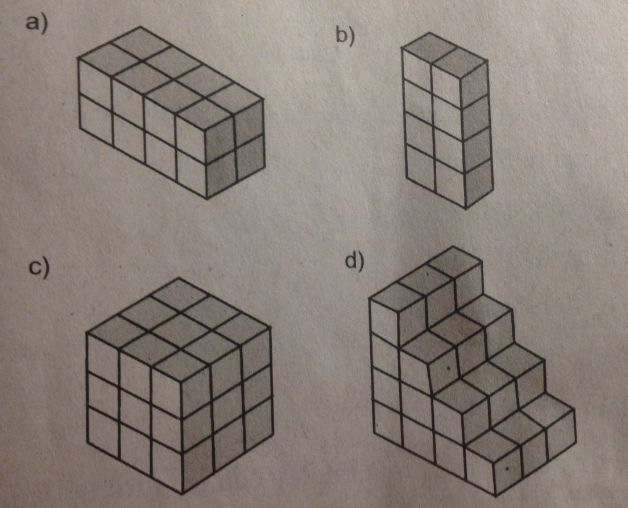
– Có 4 mặt hình chữ nhật kích thước là 4 và 2 đơn vị dài
Diện tích là: 4.(4.2) = 32 (đơn vị diện tích )
– Có 2 mặt hình vuông kích thước 2 đơn vị dài có diện tích là:
Diện tích là: 2.(2.2) = 8 (đơn vị diện tích )
Vậy diện tích của hình a là: 32 + 8 = 40 ( đơn vị diện tích )
Thể tích của hình a là : 4.2.2 = 16 ( đơn vị thể tích )
Hình b có kích thước là 4; 2 và 1 đơn vị dài
– Có 2 mặt hình chữ nhật kích thước là 4 và 2 đơn vị dài
Diện tích là 2.(4.2) = 16 ( đơn vị diện tích )
– Có 2 mặt hình chữ nhật kích thước là 4 và 1 đơn vị dài
Diện tích là: 2.(4.1) = 8 ( đơn vị diện tích )
– Có 2 mặt hình chữ nhật kích thước là 2 và 1 đơn vị dài
Diện tích là: 2.(2.1) = 4 ( đơn vị diện tích )
Vậy diện tích của hình b là: 16 + 8 + 4 = 28 ( đơn vị diện tích )
Thể tích của hình b là : 4.2.1 = 8 ( đơn vị diện tích )
Hình c có kích thước là: 3;3 và 3 đơn vị dài. Như vậy hình c bao gồm 6 mặt hình vuông kích thước là 3 và 3 đơn vị dài
Vậy diện tích của hình c là: 6. (3.3) = 54 ( đơn vị diện tích )
Thể tích của hình c là: 3.3.3 =27 ( đơn vị thể tích )
Hình d gồm:
– 8 hình chữ nhật có kích thước là 1 và 3 đơn vị dài
Diện tích là: 8. (3.1) = 24 ( đơn vị diện tích )
– 2 hình chữ nhật có kích thước là 4 và 3 đơn vị dài:
Diện tích là: 2.(4.3) = 24 ( đơn vị diện tích )
– Hai mặt bên mỗi mặt có 10 đơn vị diện tích
Vậy diện tích của hình d là:
24 + 24 + 2.10 = 68 ( đơn vị diện tích )
Cắt ghép ta được 1 hình lập phương cạnh 3 và 1 hình hộp chữ nhật kích thước 1; 1 và 3
Vậy thể tích của hình d là:
3.3.3 + 1.1.3 = 27 + 3 = 30 ( đơn vị thể tích )
Bài 25 trang 138 SBT Toán 8 tập 2
Cho các hình lăng trụ đứng với các kích thước như ở các hình 117a, b, c.
a. Hãy tìm diện tích xung quanh của mỗi hình.
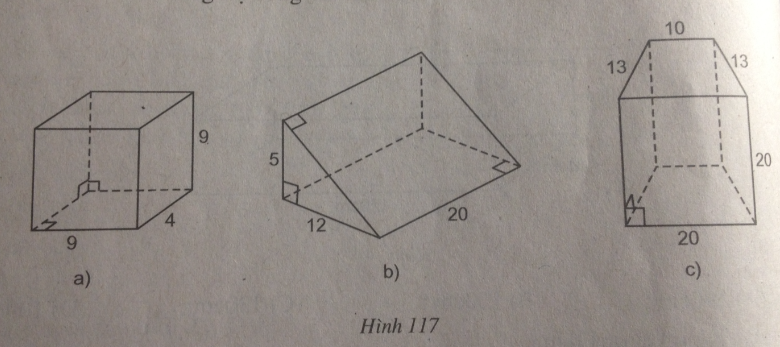
b. Hãy tìm diện tích toàn phần của mỗi hình.
HD giải: Hình a:
Diện tích xung quanh là: (9 + 4 ).2.9 = 234 ( đơn vị diện tích )
Diện tích mặt đáy là: 9.4 = 36 ( đơn vị diện tích )
Diện tích toàn phần: 234 + 36.2 = 306 ( đơn vị diện tích )
Hình b:
Áp dụng định lí Pi-ta-go, ta có: \({5^2} + {12^2} + = 25 + 144 = 169\)
Suy ra cạnh huyền của tam giác vuông bằng 13
Diện tích xung quanh là: ( 5 + 13 + 12 ).20 = 600 ( dvdt )
Diện tích mặt đáy là: \({1 \over 2}.5.12 = 30\) (đvdt)
Diện tích toàn phần là: 600 + 30.2 = 660 (đvdt)
Hình c:
Diện tích xung quanh là: (13 + 10 + 13 + 20).20 = 1120 ( đvdt)
Hình c có đáy là 1 hình thang cân, từ đáy nhỏ kẻ 2 đường thẳng vuông góc với đáy lớn, ta được 1 hình chữ nhật có cạnh bằng 10 nên 2 phần còn lại đáy lớn bằng nhau và bằng 5
Áp dụng định lí Pi-ta-go, ta có:
\({13^2} – {5^2} = 169 – 25 = 144\)
Chiều cao hình thang là 12
Diện tích đáy là: \({{10 + 20} \over 2}.12 = 180\) ( đvdt )
Diện tích toàn phần: 1120 + 180.2 = 1480 ( đvdt)
Trả lời