Giải Bài 1. Phương pháp quy nạp toán học – Chuyên đề Toán 10 CD

Giải Bài 1. Phương pháp quy nạp toán học – Chuyên đề Toán 10 CD

==============

Giải mục 1 trang 23, 24, 25 Chuyên đề học tập Toán 10 – Cánh diều>

Lựa chọn câu để xem lời giải nhanh hơn

• Câu hỏi khởi động
• Hoạt động
• Luyện tập – vận dụng 1

Câu hỏi khởi động

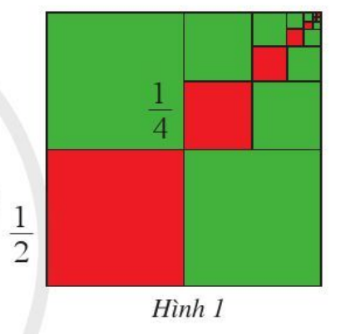
Chia hình vuông cạnh 1 thành 4 hình vuông nhỏ bằng nhau, lấy ra hình vuông nhỏ thứ nhất (ở góc dưới bên trái, màu đỏ), cạnh của hình vuông đó bằng \(\frac{1}{2}.\)

Chia hình vuông nhỏ ở góc trên bên phải thành bốn hình vuông bằng nhau, lấy ra hình vuông nhỏ thứ hai (màu đỏ), cạnh của hình vuông đó bằng \(\frac{1}{4}.\)

Tiếp tục quá trình trên ta được dãy các hình vuông nhỏ (màu đỏ) ở hình 1.

Cạnh của hình vuông nhỏ thứ n (màu đỏ) bằng bao nhiêu? Vì sao?

Lời giải chi tiết:

Nhận xét:

Chia hình vuông cạnh a thành 4 hình vuông, lấy ra hình vuông nhỏ thứ nhất (như cách lấy ở trên) thì cạnh của hình vuông đó bằng \(\frac{a}{2}\).

=> Sau mỗi lần lấy, độ lớn của cạnh hình vuông giảm đi 2 lần

=> Sau n lần, cạnh hình vuông nhỏ thứ n giảm đi \({2^n}\) so với hình ban đầu.

=> Cạnh của hình vuông nhỏ thứ n là \(\frac{1}{{{2^n}}}\)

 

Hoạt động

Xét mệnh đề chứa biến P(n): “\(1 + 3 + 5 + … + (2n – 1) = {n^2}\)” với n là số nguyên dương.

a) Chứng tỏ rằng P(1) là mệnh đề đúng.

b) Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, cho biết \(1 + 3 + 5 + … + (2k – 1)\) bằng bao nhiêu.

c) Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, chứng tỏ rằng P(k+1) cũng là mệnh đề đúng bằng cách chỉ ra \({k^2} + [2(k + 1) – 1] = {(k + 1)^2}\).

Lời giải chi tiết:

a) Mệnh đề P(1) là: “\(1 = {1^2}\)”, rõ ràng mệnh đề này đúng.

b) Mệnh đề P(k) là: “\(1 + 3 + 5 + … + (2k – 1) = {k^2}\)”

Mệnh đề P(k) đúng thì \(1 + 3 + 5 + … + (2k – 1)\) bằng \({k^2}\)

c) Mệnh đề P(k+1) là: “\(1 + 3 + 5 + … + [2(k + 1) – 1] = {(k + 1)^2}\)”

Mệnh đề P(k) đúng nên ta có \(1 + 3 + 5 + … + (2k – 1) = {k^2}\)

\(\begin{array}{l} \Rightarrow 1 + 3 + 5 + … + [2(k + 1) – 1] = 1 + 3 + 5 + … + (2k – 1) + [2(k + 1) – 1]\\ = {k^2} + [2(k + 1) – 1] = {k^2} + 2k + 1 = {(k + 1)^2}\end{array}\)

Vậy mệnh đề P(k+1) cũng đúng.

Luyện tập – vận dụng 1

Chứng minh:

a) \(\frac{1}{{\sqrt 1  + \sqrt 2 }} + \frac{1}{{\sqrt 2  + \sqrt 3 }} + … + \frac{1}{{\sqrt n  + \sqrt {n + 1} }} = \sqrt {n + 1}  – 1\) với mọi \(n \in \mathbb{N}*\)

b) \(\frac{{{2^3} – 1}}{{{2^3} + 1}}.\frac{{{3^3} – 1}}{{{3^3} + 1}}.\frac{{{4^3} – 1}}{{{4^3} + 1}}…\frac{{{n^3} – 1}}{{{n^3} + 1}} = \frac{{2({n^2} + n + 1)}}{{3n(n + 1)}}\) với mọi \(n \in \mathbb{N}*,n \ge 2\)

Phương pháp giải:

Chứng minh mệnh đề P(n) đúng với \(n \ge p\) thì:

Bước 1: Chứng tỏ mệnh đề đúng với \(n = p\)

Bước 2: Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, ta chứng tỏ P(k+1) cũng là mệnh đề đúng.

Lời giải chi tiết:

a) Ta chứng minh bằng quy nạp theo n.

Bước 1: Khi \(n = 1\) ta có \(\frac{1}{{\sqrt 1  + \sqrt 2 }} = \sqrt 2  – 1\), đúng

vì \(\left( {\sqrt 2  + \sqrt 1 } \right)\left( {\sqrt 2  – \sqrt 1 } \right) = 2 – 1 = 1 \Rightarrow \frac{1}{{\sqrt 2  + \sqrt 1 }} = \sqrt 2  – \sqrt 1  = \sqrt 2  – 1\)

 

Như vậy đẳng thức đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:

\(\frac{1}{{\sqrt 1  + \sqrt 2 }} + \frac{1}{{\sqrt 2  + \sqrt 3 }} + … + \frac{1}{{\sqrt {k + 1}  + \sqrt {k + 2} }} = \sqrt {k + 2}  – 1\)

Thật vậy, theo giả thiết quy nạp ta có:

\(\frac{1}{{\sqrt 1  + \sqrt 2 }} + \frac{1}{{\sqrt 2  + \sqrt 3 }} + … + \frac{1}{{\sqrt k  + \sqrt {k + 1} }} = \sqrt {k + 1}  – 1\)

Suy ra

\(\begin{array}{l}\frac{1}{{\sqrt 1  + \sqrt 2 }} + \frac{1}{{\sqrt 2  + \sqrt 3 }} + … + \frac{1}{{\sqrt {k + 1}  + \sqrt {k + 2} }}\\ = \sqrt {k + 1}  – 1 + \frac{1}{{\sqrt {k + 1}  + \sqrt {k + 2} }}\\ = \frac{{{{\left( {\sqrt {k + 1} } \right)}^2} + \sqrt {k + 1} .\sqrt {k + 2}  + 1}}{{\sqrt {k + 1}  + \sqrt {k + 2} }} – 1\\ = \frac{{k + 2 + \sqrt {k + 1} .\sqrt {k + 2} }}{{\sqrt {k + 1}  + \sqrt {k + 2} }} – 1\\ = \frac{{\sqrt {k + 2} \left( {\sqrt {k + 2}  + \sqrt {k + 1} } \right)}}{{\sqrt {k + 1}  + \sqrt {k + 2} }} – 1\\ = \sqrt {k + 2}  – 1\end{array}\)

Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*\). Tức là:

\(\frac{1}{{\sqrt 1  + \sqrt 2 }} + \frac{1}{{\sqrt 2  + \sqrt 3 }} + … + \frac{1}{{\sqrt n  + \sqrt {n + 1} }} = \sqrt {n + 1}  – 1\) với mọi \(n \in \mathbb{N}*\)

b) Ta chứng minh bằng quy nạp theo n.

Bước 1: Khi \(n = 2\) ta có \(\frac{{{2^3} – 1}}{{{2^3} + 1}} = \frac{{2({2^2} + 2 + 1)}}{{3.2(2 + 1)}}\), đúng

vì \(\frac{{{2^3} – 1}}{{{2^3} + 1}} = \frac{7}{9};\frac{{2({2^2} + 2 + 1)}}{{3.2(2 + 1)}} = \frac{{2.7}}{{3.2.3}} = \frac{7}{9}\)

Như vậy đẳng thức đúng với \(n = 2\)

Bước 2: Với k là một số nguyên dương lớn hơn 2 tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:

\(\frac{{{2^3} – 1}}{{{2^3} + 1}}.\frac{{{3^3} – 1}}{{{3^3} + 1}}.\frac{{{4^3} – 1}}{{{4^3} + 1}}…\frac{{{{(k + 1)}^3} – 1}}{{{{(k + 1)}^3} + 1}} = \frac{{2({{(k + 1)}^2} + (k + 1) + 1)}}{{3(k + 1)(k + 2)}}\)

Thật vậy, theo giả thiết quy nạp ta có:

\(\frac{{{2^3} – 1}}{{{2^3} + 1}}.\frac{{{3^3} – 1}}{{{3^3} + 1}}.\frac{{{4^3} – 1}}{{{4^3} + 1}}…\frac{{{{(k + 1)}^3} – 1}}{{{{(k + 1)}^3} + 1}} = \frac{{2({{(k + 1)}^2} + (k + 1) + 1)}}{{3(k + 1)(k + 2)}}\)

Suy ra

\(\begin{array}{l}\frac{{{2^3} – 1}}{{{2^3} + 1}}.\frac{{{3^3} – 1}}{{{3^3} + 1}}.\frac{{{4^3} – 1}}{{{4^3} + 1}}…\frac{{{{(k + 1)}^3} – 1}}{{{{(k + 1)}^3} + 1}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{{{(k + 1)}^3} – 1}}{{{{(k + 1)}^3} + 1}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{[(k + 1) – 1][{{(k + 1)}^2} + (k + 1) + 1]}}{{[(k + 1) + 1][{{(k + 1)}^2} – (k + 1) + 1]}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{k[{{(k + 1)}^2} + (k + 1) + 1]}}{{(k + 2)({k^2} + 2k + 1 – k – 1 + 1)}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{k[{{(k + 1)}^2} + (k + 1) + 1]}}{{(k + 2)({k^2} + k + 1)}}\\ = \frac{{2[{{(k + 1)}^2} + (k + 1) + 1]}}{{3(k + 1)(k + 2)}}\end{array}\)

Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*,n \ge 2\). Tức là:

\(\frac{{{2^3} – 1}}{{{2^3} + 1}}.\frac{{{3^3} – 1}}{{{3^3} + 1}}.\frac{{{4^3} – 1}}{{{4^3} + 1}}…\frac{{{n^3} – 1}}{{{n^3} + 1}} = \frac{{2({n^2} + n + 1)}}{{3n(n + 1)}}\) với mọi \(n \in \mathbb{N}*,n \ge 2\)

Giải mục 1 trang 23, 24, 25 Chuyên đề học tập Toán 10 – Cánh diều

Giải mục 2 trang 25, 26 Chuyên đề học tập Toán 10 – Cánh diều>

Lựa chọn câu để xem lời giải nhanh hơn

• Luyện tập – vận dụng 2
• Luyện tập – vận dụng 3

Luyện tập – vận dụng 2

Chứng minh với mọi \(n \in \mathbb{N}*,{(1 + \sqrt 2 )^n},{(1 – \sqrt 2 )^n}\) lần lượt viết được ở dạng \({a_n} + {b_n}\sqrt 2 ,{a_n} – {b_n}\sqrt 2 ,\) trong đó \({a_n},{b_n}\) là các số nguyên dương.

Phương pháp giải:

Chứng minh mệnh đề P(n) đúng với \(n \ge p\) thì:

Bước 1: Chứng tỏ mệnh đề đúng với \(n = p\)

Bước 2: Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, ta chứng tỏ P(k+1) cũng là mệnh đề đúng.

Lời giải chi tiết:

Bước 1: Khi \(n = 1\) ta có \({\left( {1 + \sqrt 2 } \right)^1} = 1 + \sqrt 2 ;{\left( {1 – \sqrt 2 } \right)^1} = 1 – \sqrt 2 \) có dạng \({a_1} + {b_1}\sqrt 2 ,{a_1} – {b_1}\sqrt 2 \) với \({a_1} = 1;{b_1} = 1\) là các số nguyên dương

Vậy mệnh đề đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà mệnh đề đúng, ta phải chứng minh mệnh đề đúng với k+1, tức là:

\({\left( {1 + \sqrt 2 } \right)^{k + 1}};{\left( {1 – \sqrt 2 } \right)^{k + 1}}\) có dạng \({a_{k + 1}} + {b_{k + 1}}\sqrt 2 ;{a_{k + 1}} – {b_{k + 1}}\sqrt 2 \) với \({a_{k + 1}};{b_{k + 1}}\) là các số nguyên dương.

Thật vậy, theo giả thiết quy nạp ta có:

\({\left( {1 + \sqrt 2 } \right)^k} = {a_k} + {b_k}\sqrt 2 ;{\left( {1 – \sqrt 2 } \right)^k} = {a_k} – {b_k}\sqrt 2 \) với \({a_k};{b_k}\) là các số nguyên dương.

Suy ra

\(\begin{array}{l}{\left( {1 + \sqrt 2 } \right)^{k + 1}} = {\left( {1 + \sqrt 2 } \right)^k}\left( {1 + \sqrt 2 } \right)\\ = \left( {{a_k} + {b_k}\sqrt 2 } \right)\left( {1 + \sqrt 2 } \right) = {a_k} + {b_k}\sqrt 2  + {a_k}\sqrt 2  + {b_k}{\left( {\sqrt 2 } \right)^2}\\ = \left( {{a_k} + 2{b_k}} \right) + \left( {{a_k} + {b_k}} \right)\sqrt 2 \\ = {a_{k + 1}} + {b_{k + 1}}\sqrt 2 \end{array}\)

Trong đó \({a_{k + 1}} = {a_k} + 2{b_k} \in \mathbb{N}*;{b_{k + 1}} = {a_k} + {b_k} \in \mathbb{N}*\)

Vậy mệnh đề đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, mệnh đề đúng với mọi \(n \in \mathbb{N}*\).

Luyện tập – vận dụng 3

Chứng minh \({16^n} – 15n – 1\) chia hết cho 225 với mọi \(n \in \mathbb{N}*\).

Phương pháp giải:

Chứng minh mệnh đề P(n) đúng với \(n \ge p\) thì:

Bước 1: Chứng tỏ mệnh đề đúng với \(n = p\)

Bước 2: Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, ta chứng tỏ P(k+1) cũng là mệnh đề đúng.

Lời giải chi tiết:

Bước 1: Khi \(n = 1\) ta có \({16^1} – 15.1 – 1 = 0\) chia hết cho 225.

Vậy mệnh đề đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà mệnh đề đúng, ta phải chứng minh mệnh đề đúng với k+1, tức là:

\({16^{k + 1}} – 15(k + 1) – 1\) chia hết cho 225.

Thật vậy, theo giả thiết quy nạp ta có:

\({16^k} – 15k – 1\) chia hết cho 225.

Suy ra

\(\begin{array}{l}{16^{k + 1}} – 15(k + 1) – 1 = {16.16^k} – 15k – 16\\ = 16\left( {{{16}^k} – 15k – 1} \right) + 16(15k + 1) – 15k – 16\\ = 16\left( {{{16}^k} – 15k – 1} \right) + 225k\end{array}\)

Chia hết cho 225

Vậy mệnh đề đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, mệnh đề đúng với mọi \(n \in \mathbb{N}*\).

Giải mục 2 trang 25, 26 Chuyên đề học tập Toán 10 – Cánh diều
=================

Giải bài 1 trang 29 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Cho \({S_n} = 1 + 2 + {2^2} + … + {2^n}\) và \({T_n} = {2^{n + 1}} – 1\), với \(n \in \mathbb{N}*\)

a) So sánh \({S_1}\) và \({T_1}\); \({S_2}\) và \({T_2}\);\({S_3}\) và \({T_3}\).

b) Dự đoán công thức tính \({S_n}\) và chứng minh bằng phương pháp quy nạp toán học.

Phương pháp giải

Phương pháp quy nạp: Chứng minh mệnh đề đúng với \(n \ge p\)

Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)

Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.

Lời giải chi tiết

a) \({S_1} = 1 + 2 = 3\); \({T_1} = {2^{1 + 1}} – 1 = 3\)

Do đó \({S_1} = {T_1}\)

\({S_2} = 1 + 2 + {2^2} = 7\); \({T_2} = {2^{2 + 1}} – 1 = 7\)

Do đó \({S_2} = {T_2}\)

\({S_3} = 1 + 2 + {2^2} + {2^3} = 15\); \({T_3} = {2^{3 + 1}} – 1 = 15\)

Do đó \({S_3} = {T_3}\)

b) Dự doán: \({S_n} = {T_n}\) từ đó có công thức tính \({S_n} = {2^{n + 1}} – 1\)

Chứng minh:

Bước 1: Khi \(n = 1\) ta có \({S_1} = {T_1} = {2^2} – 1\) đúng

Như vậy đẳng thức đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:

\({S_{k + 1}} = {2^{(k + 1) + 1}} – 1\) hay \({S_{k + 1}} = {2^{k + 2}} – 1\)

Thật vậy, theo giả thiết quy nạp ta có:

\({S_k} = {2^{k + 1}} – 1\)

Suy ra

\(\begin{array}{l}{S_{k + 1}} = 1 + 2 + {2^2} + … + {2^{k + 1}} = {S_k} + {2^{k + 1}}\\ = {2^{k + 1}} – 1 + {2^{k + 1}} = {2.2^{k + 1}} – 1 = {2^{k + 2}} – 1\end{array}\)

Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*\).

 

Giải bài 1 trang 29 Chuyên đề học tập Toán 10 – Cánh diều
=============

Giải bài 2 trang 29 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Cho \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + … + \frac{1}{{{2^n}}}\) và \({T_n} = 2 – \frac{1}{{{2^n}}}\), với \(n \in \mathbb{N}*\)

a) So sánh \({S_1}\) và \({T_1}\); \({S_2}\) và \({T_2}\);\({S_3}\) và \({T_3}\).

b) Dự đoán công thức tính \({S_n}\) và chứng minh bằng phương pháp quy nạp toán học.

Phương pháp giải

Phương pháp quy nạp: Chứng minh mệnh đề đúng với \(n \ge p\)

Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)

Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.

Lời giải chi tiết

a) \({S_1} = 1 + \frac{1}{2} = \frac{3}{2}\); \({T_1} = 2 – \frac{1}{{{2^1}}} = \frac{3}{2}\)

Do đó \({S_1} = {T_1}\)

\({S_2} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} = \frac{7}{4}\); \({T_2} = 2 – \frac{1}{{{2^2}}} = \frac{7}{4}\)

Do đó \({S_2} = {T_2}\)

\({S_3} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} = \frac{{15}}{8}\); \({T_3} = 2 – \frac{1}{{{2^3}}} = \frac{{15}}{8}\)

Do đó \({S_3} = {T_3}\)

b) Dự doán: \({S_n} = {T_n}\) từ đó có công thức tính \({S_n} = 2 – \frac{1}{{{2^n}}}\)

Chứng minh:

Bước 1: Khi \(n = 1\) ta có \({S_1} = 2 – \frac{1}{{{2^1}}}\) đúng

Như vậy đẳng thức đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:

\({S_{k + 1}} = 2 – \frac{1}{{{2^{k + 1}}}}\)

Thật vậy, theo giả thiết quy nạp ta có:

\({S_k} = 2 – \frac{1}{{{2^k}}}\)

Suy ra

\(\begin{array}{l}{S_{k + 1}} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + … + \frac{1}{{{2^{k + 1}}}} = {S_k} + \frac{1}{{{2^{k + 1}}}}\\ = 2 – \frac{1}{{{2^k}}} + \frac{1}{{{2^{k + 1}}}} = 2 – \frac{2}{{{2^{k + 1}}}} + \frac{1}{{{2^{k + 1}}}} = 2 – \frac{1}{{{2^{k + 1}}}}\end{array}\)

Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*\).

 

Giải bài 2 trang 29 Chuyên đề học tập Toán 10 – Cánh diều
=============

Giải bài 3 trang 29 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Cho \({S_n} = \frac{1}{{1.5}} + \frac{1}{{5.9}} + \frac{1}{{9.13}} + … + \frac{1}{{(4n – 3)(4n + 1)}}\) với \(n \in \mathbb{N}*\)

a) Tính \({S_1}\); \({S_2}\);\({S_3}\); \({S_4}\).

b) Dự đoán công thức tính \({S_n}\) và chứng minh bằng phương pháp quy nạp toán học.

Phương pháp giải

Phương pháp quy nạp: Chứng minh mệnh đề đúng với \(n \ge p\)

Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)

Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.

Lời giải chi tiết

a) \(n = 1 \Rightarrow 4n – 3 = 1;4n + 1 = 5 \Rightarrow {S_1} = \frac{1}{{1.5}} = \frac{1}{5}\);

\({S_2} = \frac{1}{{1.5}} + \frac{1}{{5.9}} = \frac{2}{9}\);

\({S_3} = \frac{1}{{1.5}} + \frac{1}{{5.9}} + \frac{1}{{9.13}} = \frac{3}{{13}}\);

b) Ta có:

\({S_1} = \frac{1}{5} = \frac{1}{{4.1 + 1}};\)\({S_2} = \frac{2}{{4.2 + 1}};\)\({S_3} = \frac{3}{{4.3 + 1}};\)

Dự doán: \({S_n} = \frac{n}{{4.n + 1}}\)

Chứng minh:

Bước 1: Khi \(n = 1\) ta có \({S_1} = \frac{1}{{4.1 + 1}}\) đúng

Như vậy đẳng thức đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:

\({S_{k + 1}} = \frac{{k + 1}}{{4.(k + 1) + 1}}\) hay \({S_{k + 1}} = \frac{{k + 1}}{{4k + 5}}\)

Thật vậy, theo giả thiết quy nạp ta có:

\({S_k} = \frac{k}{{4.k + 1}}\)

Suy ra

\(\begin{array}{l}{S_{k + 1}} = \frac{1}{{1.5}} + \frac{1}{{5.9}} + \frac{1}{{9.13}} + … + \frac{1}{{(4k – 3)(4k + 1)}} + \frac{1}{{[4(k + 1) – 3][4(k + 1) + 1]}}\\ = {S_k} + \frac{1}{{(4k + 1)(4k + 5)}} = \frac{k}{{4k + 1}} + \frac{1}{{(4k + 1)(4k + 5)}}\\ = \frac{{k(4k + 5)}}{{(4k + 1)(4k + 5)}} + \frac{1}{{(4k + 1)(4k + 5)}}\\ = \frac{{4{k^2} + 5k + 1}}{{(4k + 1)(4k + 5)}} = \frac{{(4k + 1)(k + 1)}}{{(4k + 1)(4k + 5)}} = \frac{{k + 1}}{{4k + 5}}\end{array}\)

Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*\).

Giải bài 3 trang 29 Chuyên đề học tập Toán 10 – Cánh diều
——————-

Giải bài 4 trang 29 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Cho q là số thực khác 1. Chứng minh: \(1 + q + {q^2} + … + {q^{n – 1}} = \frac{{1 – {q^n}}}{{1 – q}}\) với mọi \(n \in \mathbb{N}*\)

Phương pháp giải

Phương pháp quy nạp: Chứng minh mệnh đề đúng với \(n \ge p\)

Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)

Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.

Lời giải chi tiết

Bước 1: Khi \(n = 1\) ta có \(1 = \frac{{1 – {q^1}}}{{1 – q}}\) hiển nhiên đúng với \(q \ne 1\)

Như vậy đẳng thức đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:

\(1 + q + {q^2} + … + {q^{k – 1}} + {q^k} = \frac{{1 – {q^{k + 1}}}}{{1 – q}}\)

Thật vậy, theo giả thiết quy nạp ta có:

\(1 + q + {q^2} + … + {q^{k – 1}} = \frac{{1 – {q^k}}}{{1 – q}}\)

Suy ra

\(\begin{array}{l}1 + q + {q^2} + … + {q^{k – 1}} + {q^k} = \frac{{1 – {q^k}}}{{1 – q}} + {q^k}\\ = \frac{{1 – {q^k}}}{{1 – q}} + \frac{{{q^k} – {q^{k + 1}}}}{{1 – q}} = \frac{{1 – {q^k} + {q^k} – {q^{k + 1}}}}{{1 – q}} = \frac{{1 – {q^{k + 1}}}}{{1 – q}}\end{array}\)

Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*\).

 

 

Giải bài 4 trang 29 Chuyên đề học tập Toán 10 – Cánh diều
———————-

Giải bài 5 trang 29 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Chứng minh với mọi \(n \in \mathbb{N}*\), ta có:

a) \({13^n} – 1\) chia hết cho 6.

b) \({4^n} + 15n – 1\) chia hết cho 9.

Phương pháp giải

Chứng minh mệnh đề đúng với \(n \ge p\) thì:

Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)

Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.

Lời giải chi tiết

a)

Bước 1: Khi \(n = 1\) ta có \({13^1} – 1 = 12\) chia hết cho 6.

Vậy mệnh đề đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà mệnh đề đúng, ta phải chứng minh mệnh đề đúng với k+1, tức là:

\({13^{k + 1}} – 1\) chia hết cho 6.

Thật vậy, theo giả thiết quy nạp ta có:

\({13^k} – 1\) chia hết cho 6.

Suy ra

\({13^{k + 1}} – 1 = {13.13^k} – 1 = 13.\left( {{{13}^k} – 1} \right) + 12\) chia hết cho 6

Vậy mệnh đề đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, mệnh đề đúng với mọi \(n \in \mathbb{N}*\).

b)

Bước 1: Khi \(n = 1\) ta có \({4^1} + 15.1 – 1 = 18\) chia hết cho 9.

Vậy mệnh đề đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà mệnh đề đúng, ta phải chứng minh mệnh đề đúng với k+1, tức là:

\({4^{k + 1}} + 15.(k + 1) – 1\) chia hết cho 9.

Thật vậy, theo giả thiết quy nạp ta có:

\({4^k} + 15k – 1\) chia hết cho 9.

Suy ra

\({4^{k + 1}} + 15.(k + 1) – 1 = {4.4^k} + 15k + 14 = 4\left( {{4^k} + 15k – 1} \right) – 45k + 18\) chia hết cho 9

Vậy mệnh đề đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, mệnh đề đúng với mọi \(n \in \mathbb{N}*\).

 

 

Giải bài 5 trang 29 Chuyên đề học tập Toán 10 – Cánh diều
——————–

Giải bài 6 trang 29 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Chứng minh \({n^n} > {(n + 1)^{n – 1}}\) với mọi \(n \in \mathbb{N}*,n \ge 2.\)

Phương pháp giải

Phương pháp quy nạp: Chứng minh mệnh đề đúng với \(n \ge p\)

Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)

Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.

Lời giải chi tiết

Bước 1: Khi \(n = 2\) ta có \({2^2} > {(2 + 1)^{2 – 1}}\) hay \(4 > 3\)hiển nhiên đúng

Như vậy bất đẳng thức đúng với \(n = 2\)

Bước 2: Với k là một số nguyên dương tùy ý mà bất đẳng thức đúng, ta phải chứng minh bất đẳng thức đúng với k+1, tức là:

\({(k + 1)^{k + 1}} > {(k + 1 + 1)^{k + 1 – 1}}\) hay \({(k + 1)^{k + 1}} > {(k + 2)^k}\)

Thật vậy, theo giả thiết quy nạp ta có:

\({k^k} > {(k + 1)^{k – 1}}\)

Suy ra

\({k^k}{(k + 1)^{k + 1}} > {(k + 1)^{k – 1}}{(k + 1)^{k + 1}} = {(k + 1)^{k – 1 + k + 1}} = {(k + 1)^{2k}}\)

Mà \({(k + 1)^{2k}} = {\left[ {{{(k + 1)}^2}} \right]^k} = {\left( {{k^2} + 2k + 1} \right)^k} > {\left( {{k^2} + 2k} \right)^k}\)

\( \Rightarrow {k^k}{(k + 1)^{k + 1}} > {\left( {{k^2} + 2k} \right)^k} = {\left[ {k.(k + 2)} \right]^k} = {k^k}.{(k + 2)^k}\)

\( \Rightarrow {(k + 1)^{k + 1}} > {(k + 2)^k}\)

Vậy bất đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, bất đẳng thức đúng với mọi \(n \in \mathbb{N}*\).

 

Giải bài 6 trang 29 Chuyên đề học tập Toán 10 – Cánh diều
—————-

Giải bài 7 trang 29 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Chứng minh \({a^n} – {b^n} = (a – b)({a^{n – 1}} + {a^{n – 2}}b + … + a{b^{n – 2}} + {b^{n – 1}})\) với mọi \(n \in \mathbb{N}*\)

Phương pháp giải

Phương pháp quy nạp: Chứng minh mệnh đề đúng với \(n \ge p\)

Bước 1: Kiểm tra mệnh đề là đúng với \(n = p\)

Bước 2: Giả thiết mệnh đề đúng với số tự nhiên \(n = k \ge p\) và chứng minh mệnh đề đúng với \(n = k + 1.\) Kết luận.

Lời giải chi tiết

Bước 1: Khi \(n = 1\) ta có \({a^1} – {b^1} = a – b\) hiển nhiên đúng

Như vậy đẳng thức đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:

\({a^{k + 1}} – {b^{k + 1}} = (a – b)({a^{k + 1 – 1}} + {a^{k + 1 – 2}}b + … + a{b^{k + 1 – 2}} + {b^{k + 1 – 1}})\) hay \({a^{k + 1}} – {b^{k + 1}} = (a – b)({a^k} + {a^{k – 1}}b + … + a{b^{k – 1}} + {b^k})\)

Thật vậy, theo giả thiết quy nạp ta có:

\({a^k} – {b^k} = (a – b)({a^{k – 1}} + {a^{k – 2}}b + … + a{b^{k – 2}} + {b^{k – 1}})\)

Suy ra

\(\begin{array}{l}{a^{k + 1}} – {b^{k + 1}} = a.{a^k} – b.{b^k} = a\left( {{a^k} – {b^k}} \right) + a{b^k} – b.{b^k} = a\left( {{a^k} – {b^k}} \right) + \left( {a – b} \right).{b^k}\\ = a.(a – b)({a^{k – 1}} + {a^{k – 2}}b + … + a{b^{k – 2}} + {b^{k – 1}}) + \left( {a – b} \right).{b^k}\\ = (a – b)\left[ {a({a^{k – 1}} + {a^{k – 2}}b + … + a{b^{k – 2}} + {b^{k – 1}}) + {b^k}} \right]\\ = (a – b)({a^k} + {a^{k – 1}}b + … + a{b^{k – 1}} + {b^k})\end{array}\)

Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*\).

Giải bài 7 trang 29 Chuyên đề học tập Toán 10 – Cánh diều
——————–

Giải bài 8 trang 29 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Cho tam giác đều màu xanh (Hình thứ nhất)

a) Nêu quy luật chọn tam giác đều màu trắng ở Hình thứ hai

b) Nêu quy luật chọn các tam giác đều màu trắng ở Hình thứ ba

c) Nêu quy luật chọn các tam giác đều màu trắng từ Hình thứ tư và các tam giác đều màu trắng ở những hình sau đó.

d) Tính số tam giác đều màu xanh lần lượt trong các Hình thứ nhất, Hình thứ hai, Hình thứ ba.

e) Dự đoán số tam giác đều màu xanh trong Hình thứ n. Chứng minh kết quả đó banwggf phương pháp quy nạp toán học.

 

Lời giải chi tiết

a) Cách chọn tam giác đều màu trắng ở Hình thứ hai

Bước 1: Tìm trung điểm các cạnh => được 3 trung điểm

Bước 2: Tô màu trắng cho tam giác có 3 đỉnh là 3 trung điểm ấy.

b) Nêu quy luật chọn các tam giác đều màu trắng ở Hình thứ ba

Từ mỗi tam giác xanh của Hình thứ hai, ta thực hiện các bước:

Bước 1: Tìm trung điểm các cạnh => được 3 trung điểm

Bước 2: Tô màu trắng cho tam giác có 3 đỉnh là 3 trung điểm ấy.

c) Quy luật chọn các tam giác đều màu trắng từ Hình thứ tư và các tam giác đều màu trắng ở những hình sau đó.

Từ mỗi tam giác xanh của Hình thứ ba, ta thực hiện các bước:

Bước 1: Tìm trung điểm các cạnh => được 3 trung điểm

Bước 2: Tô màu trắng cho tam giác có 3 đỉnh là 3 trung điểm ấy.

Quy luật chọn các tam giác đều màu trắng ở hình thứ n đó:

Từ mỗi tam giác xanh của Hình thứ (n-1), ta thực hiện các bước:

Bước 1: Tìm trung điểm các cạnh => được 3 trung điểm

Bước 2: Tô màu trắng cho tam giác có 3 đỉnh là 3 trung điểm ấy.

d) Hình thứ nhất có 1 tam giác đều màu xanh

Hình thứ hai có 3 tam giác đều màu xanh

Hình thứ ba có 9 tam giác đều màu xanh

 

e) Vì Hình thứ nhất có \(1 = {3^0}\) tam giác đều màu xanh

Hình thứ hai có \(3 = {3^1}\) tam giác đều màu xanh

Hình thứ ba có \(9 = {3^2}\) tam giác đều màu xanh

Dự đoán Hình thứ n có \({3^{n – 1}}\) tam giác đều màu xanh

Chứng minh:

Bước 1: Khi \(n = 1\) ta có Hình thứ nhất có \({3^{1 – 1}}\) tam giác đều màu xanh, đúng.

Như vậy mệnh đề đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà mệnh đề đúng, ta phải chứng minh mệnh đề đúng với k+1, tức là:

Hình thứ k+1 có \({3^{k + 1 – 1}}\) tam giác đều màu xanh

Hay “Hình thứ k+1 có \({3^k}\) tam giác đều màu xanh”

Thật vậy, theo giả thiết quy nạp ta có:

Hình thứ k có \({3^{k – 1}}\) tam giác đều màu xanh

Nhận xét: Theo quy luật thì mỗi hình màu xanh sẽ được chia thành 4 tam giác đều ở hình sau, trong đó tô 1 tam giác đều màu trắng và 3 tam giác đều màu xanh. Nói cách khác, mỗi tam giác đều màu xanh sẽ chia thành 3 tam giác đều (nhỏ hơn) màu xanh ở hình tiếp theo.

Mà có \({3^{k – 1}}\) tam giác đều màu xanh

\( \Rightarrow \) Số tam giác đều màu xanh trong Hình thứ k+1 là: \({3.3^{k – 1}} = {3^{1 + k – 1}} = {3^k}\)

Vậy mệnh đề đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, mệnh đề đúng với mọi \(n \in \mathbb{N}*\).

 

Giải bài 8 trang 29 Chuyên đề học tập Toán 10 – Cánh diều
—————

Giải bài 9 trang 30 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Quan sát Hình 6

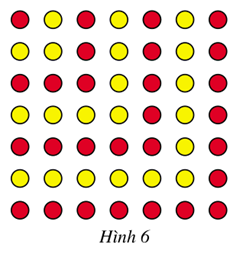
a) Nêu quy luật sắp xếp các chấm đỏ và vàng xen kẽ nhau khi xếp các chấm đó từ góc trên bên trái xuống góc dưới bên phải (tạo thành hình vuông)

b) Giả sử hình vuông thứ n có mỗi cạnh chứa n chấm. Tính tổng số chấm được xếp trong hình vuông (kể cả trên cạnh). Chứng minh kết quả đó bằng phương pháp quy nạp toán học.

Lời giải chi tiết

a) Đầu tiên xếp 1 chấm đỏ.

Xếp 3 chấm màu vàng vào phía bên phải và bên dưới chấm đỏ để tạo thành 1 hình vuông.

Xếp 5 chấm màu đỏ vào phía bên phải và bên dưới các chấm trước đó để tạo thành 1 hình vuông.

Xếp 7 chấm màu vàng vào phía bên phải và bên dưới các chấm trước đó để tạo thành 1 hình vuông.

…

Cứ như vậy, các chấm đỏ và vàng được xếp xen kẽ nhau tạo thành 1 hình vuông.

Trong đó số chấm thêm vào để tạo thành hình vuông là các số lẻ liên tiếp bắt đầu từ 1.

b) Nhận xét: Hình vuông thứ n mỗi cạnh có n chấm. Hình vuông này được tạo bởi n hàng, trong mỗi hàng có n chấm

=> Số chấm được xếp trong hình vuông (kể cả trên cạnh) là \(n.n = {n^2}\) (chấm)

Mặt khác: Theo cách xếp thì số chấm để tạo thành hình vuông thứ n là: \(1 + 3 + 5 + … + (2n – 1)\)

Ta chứng minh \(1 + 3 + 5 + … + (2n – 1) = {n^2}\) bằng phương pháp quy nạp.

Bước 1: Khi \(n = 1\) ta có \(1 = {1^2}\) hiển nhiên đúng

Như vậy đẳng thức đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:

\(1 + 3 + 5 + … + \left[ {2(k + 1) – 1} \right] = {(k + 1)^2}\) hay \(1 + 3 + 5 + … + (2k + 1) = {(k + 1)^2}\)

Thật vậy, theo giả thiết quy nạp ta có:

\(1 + 3 + 5 + … + (2k – 1) = {k^2}\)

Suy ra

\(1 + 3 + 5 + … + (2k + 1) = {k^2} + (2k + 1) = {(k + 1)^2}\)

Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*\).

 

Giải bài 9 trang 30 Chuyên đề học tập Toán 10 – Cánh diều
—————–

Giải bài 10 trang 30 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Giả sử năm đầu tiên, cô Hạnh gửi vào ngân hàng A (đồng) với lãi suất r

Lời giải chi tiết

Ta chứng minh “Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau n (năm) là \({T_n} = \frac{{A(100 + r)}}{r}\left[ {{{\left( {1 + \frac{r}{{100}}} \right)}^n} – 1} \right]\) (đồng)” bằng phương pháp quy nạp.

Bước 1: Khi \(n = 1\) ta có

Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau 1 năm là: \(A + r% .A = A.\left( {1 + \frac{r}{{100}}} \right) = \frac{{A(100 + r)}}{{100}}\)(đồng)

Và \({T_1} = \frac{{A(100 + r)}}{r}\left[ {{{\left( {1 + \frac{r}{{100}}} \right)}^1} – 1} \right] = \frac{{A(100 + r)}}{r}.\frac{r}{{100}} = \frac{{A(100 + r)}}{{100}}\)(đồng)

Như vậy mệnh đề đúng với \(n = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà mệnh đề đúng, ta phải chứng minh mệnh đề đúng với k+1, tức là:

“Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau \(k + 1\) năm là: \({T_{k + 1}} = \frac{{A(100 + r)}}{r}\left[ {{{\left( {1 + \frac{r}{{100}}} \right)}^{k + 1}} – 1} \right]\) (đồng)”

Thật vậy, theo giả thiết quy nạp ta có:

Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau \(k\) năm là: \({T_k} = \frac{{A(100 + r)}}{r}\left[ {{{\left( {1 + \frac{r}{{100}}} \right)}^k} – 1} \right]\) (đồng)

Cô không rút ra mà gửi thêm A đồng nữa

=> Số tiền gốc sau \(k + 1\) năm là: \({T_k} + A\)(đồng)

=> Số tiền lãi sau \(k + 1\) năm là: \(\left( {{T_k} + A} \right).r% \)(đồng)

Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau \(k + 1\) năm là:

\(\begin{array}{l}{T_k} + A + \left( {{T_k} + A} \right).r%  = \left( {{T_k} + A} \right).(1 + r% ) = \left( {{T_k} + A} \right)\left( {1 + \frac{r}{{100}}} \right)\\ = \left\{ {\frac{{A(100 + r)}}{r}\left[ {{{\left( {1 + \frac{r}{{100}}} \right)}^k} – 1} \right] + A} \right\}.\left( {1 + \frac{r}{{100}}} \right)\\ = \frac{{A(100 + r)}}{r}\left[ {{{\left( {1 + \frac{r}{{100}}} \right)}^k} – 1} \right].\left( {1 + \frac{r}{{100}}} \right) + A.\left( {1 + \frac{r}{{100}}} \right)\\ = \frac{{A(100 + r)}}{r}.\left[ {{{\left( {1 + \frac{r}{{100}}} \right)}^{k + 1}} – \left( {1 + \frac{r}{{100}}} \right)} \right] + A.\left( {\frac{{100 + r}}{{100}}} \right)\\ = \frac{{A(100 + r)}}{r}.\left[ {{{\left( {1 + \frac{r}{{100}}} \right)}^{k + 1}} – \left( {1 + \frac{r}{{100}}} \right)} \right] + A.\left( {\frac{{100 + r}}{r}} \right).\frac{r}{{100}}\\ = \frac{{A(100 + r)}}{r}.\left[ {{{\left( {1 + \frac{r}{{100}}} \right)}^{k + 1}} – \left( {1 + \frac{r}{{100}}} \right) + \frac{r}{{100}}} \right]\\ = \frac{{A(100 + r)}}{r}.\left[ {{{\left( {1 + \frac{r}{{100}}} \right)}^{k + 1}} – 1} \right]\end{array}\)

Vậy mệnh đề đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, mệnh đề đúng với mọi \(n \in \mathbb{N}*\).

 

Giải bài 10 trang 30 Chuyên đề học tập Toán 10 – Cánh diều
—————-

Giải bài 11 trang 30 Chuyên đề học tập Toán 10 – Cánh diều>

Đề bài

Một người gửi số tiền A (đồng) vào ngân hàng. Biểu lãi suất của ngân hàng như sau:

Chia mỗi năm thành m kì hạn và lãi suất r

Lời giải chi tiết

Ta chứng minh: “Số tiền nhận được (bao gồm cả vốn lẫn lãi) sau p (kì hạn) gửi là \({T_p} = A.{\left( {1 + \frac{r}{{100m}}} \right)^p}\) (đồng).”

Như vậy, do mỗi năm có m kì hạn nên sau n năm tương ứng là m.n kì hạn, từ đó ta suy ra số tiền nhận được (bao gồm cả vốn lẫn lãi) sau n (năm) gửi là \({S_n} = {T_{m.n}} = A.{\left( {1 + \frac{r}{{100m}}} \right)^{m.n}}\) (đồng), là điều phải chứng minh.

+ Chứng minh: “Số tiền nhận được (bao gồm cả vốn lẫn lãi) sau p (kì hạn) gửi là \({T_p} = A.{\left( {1 + \frac{r}{{100m}}} \right)^p}\) (đồng).”

Bước 1: Khi \(p = 1\) ta có

Lãi suất của m kì hạn (hay 1 năm) là r

Số tiền nhận được (bao gồm cả vốn lẫn lãi) sau 1 (kì hạn) gửi là: \(A + A.\frac{r}{{100m}} = A{\left( {1 + \frac{r}{{100m}}} \right)^1} = {T_1}\) (đồng)

Như vậy mệnh đề đúng với \(p = 1\)

Bước 2: Với k là một số nguyên dương tùy ý mà mệnh đề đúng, ta phải chứng minh mệnh đề đúng với k+1, tức là:

“Số tiền nhận được (bao gồm cả vốn lẫn lãi) sau \(k + 1\) (kì hạn) gửi là \({T_{k + 1}} = A.{\left( {1 + \frac{r}{{100m}}} \right)^{k + 1}}\) (đồng).”

Thật vậy, theo giả thiết quy nạp ta có:

“Số tiền nhận được (bao gồm cả vốn lẫn lãi) sau k (kì hạn) gửi là \({T_k} = A.{\left( {1 + \frac{r}{{100m}}} \right)^k}\) (đồng).”

=> Số tiền nhận được (bao gồm cả vốn lẫn lãi) sau \(k + 1\) (kì hạn) gửi là:

\(\begin{array}{l}A.{\left( {1 + \frac{r}{{100m}}} \right)^k} + A.{\left( {1 + \frac{r}{{100m}}} \right)^k}.\frac{r}{{100m}}\\ = A.{\left( {1 + \frac{r}{{100m}}} \right)^k}\left( {1 + \frac{r}{{100m}}} \right)\\ = A.{\left( {1 + \frac{r}{{100m}}} \right)^{k + 1}} = {T_{k + 1}}\end{array}\)

Vậy mệnh đề đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, mệnh đề đúng với mọi \(p \in \mathbb{N}*\).

Như vậy sau n năm (tương ứng là m.n kì hạn) thì số tiền nhận được (bao gồm cả vốn lẫn lãi) là \({S_n} = A.{\left( {1 + \frac{r}{{100m}}} \right)^{m.n}}\)(đồng).

Giải bài 11 trang 30 Chuyên đề học tập Toán 10 – Cánh diều