Giải SBT BÀI 3 Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác (C3 Toán 7 – Chân trời)

Giải SBT BÀI 3 Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác (C3 Toán 7 – Chân trời)
————

Giải bài 1 trang 60 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

Hãy điền vào chỗ chấm để mô tả hình bên:

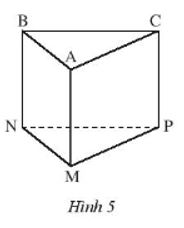
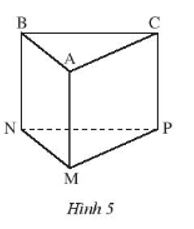
– Hình ABC.MNP (Hình 5) là hình ………….

– Các đỉnh là: ………………………………………..

– Các mặt bên là: …………………………………..

– Các cạnh bên là: …………………………………

– Hai mặt đáy là mặt ……. và mặt ……………

– Độ dài cạnh AM được gọi là ………………. của hình lăng trụ.

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Áp dụng tính chất của cạnh, góc, đỉnh, mặt bên hình lăng trụ đứng tam giác

Lời giải chi tiết

Quan sát Hình 5, ta điền được như sau:

– Hình ABC.MNP (Hình 5) là hình  lăng trụ đứng tam giác.

– Các đỉnh là:  A, B, C, M, N, P.

– Các mặt bên là:  ABNM, ACPM, BCPN.

– Các cạnh bên là:  AM, BN, CP.

– Hai mặt đáy là mặt  ABC  và mặt  MNP.

– Độ dài cạnh AM được gọi là  chiều cao  của hình lăng trụ. 

–>

— *****

Giải bài 2 trang 60 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

Cho hình lăng trụ đứng tứ giác như Hình 6.

a) Chỉ rõ hai mặt đáy và các mặt bên của hình lăng trụ.

b) Gọi tên các cạnh bên của hình lăng trụ.

c) Chiều cao của hình lăng trụ bằng độ dài đoạn thẳng nào?

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

Sử dụng tính chất của cạnh, góc của hình lăng trụ đứng tam giác 

Lời giải chi tiết

Do hình lăng trụ đứng tứ giác có các mặt bên là hình chữ nhật, do đó ta có:

a) Hai mặt đáy của hình lăng trụ là: mặt ADHE và mặt BCGF. (do các mặt này không là hình chữ nhật, nên nó phải là mặt đáy).

Bốn mặt bên của hình lăng trụ là: mặt ABFE, mặt EFGH, mặt CDHG và mặt ABCD. (là các hình chữ nhật)

b) Các cạnh bên của hình lăng trụ là: AB, EF, HG, DC.

c) Chiều cao của hình lăng trụ bằng chiều cao của cách cạnh bên.

Do đó ta có thể nói chiều cao của hình lăng trụ bằng độ dài đoạn thẳng AB (hoặc EF, hoặc HG, hoặc DC).

–>

— *****

Giải bài 3 trang 60 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

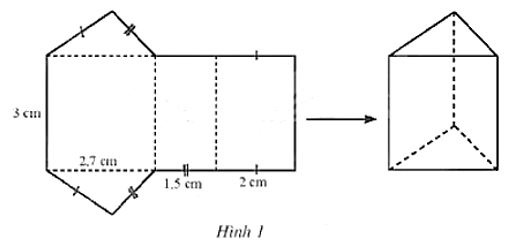
Tạo lập hình lăng trụ đứng tam giác có các cạnh đáy là 2,7 cm, 1,5 cm, 2 cm và chiều cao 3 cm.

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

– Trên tấm bìa, vẽ 3 hình chữ nhật và 2 tam giác với kích thước như Hình 1.

– Gấp theo các đường nét đứt ta được hình phải tạo lập.

Lời giải chi tiết

–>

— *****

Giải bài 4 trang 60 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

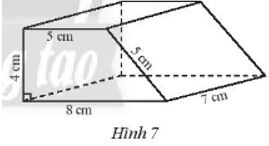
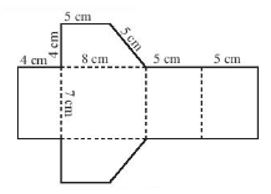
Tạo lập hình lăng trục đứng tứ giác có các số đo như Hình 7.

a) Cho biết chiều cao của hình lăng trụ.

b) Tạo lập hình lăng trụ.

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

a) Hình 7 mô tả hình lăng trụ đứng tứ giác có các mặt bên là hình chữ nhật có kích thước là 5 cm, 7 cm và đáy là hình thang vuông có kích thước là 5 cm, 8 cm và 4 cm.

b) Trên tấm bìa vẽ 2 hình thang và 4 hình chữ nhật như dưới đây, rồi gấp theo các nét đứt ta được hình cần tạo lập.

Lời giải chi tiết

a) Chiều cao của hình lăng trụ là 7 cm.

b)

–>

— *****

Giải bài 5 trang 60 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

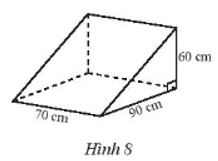
Cho hình lăng trụ đứng tam giác như Hình 8.

a) Chiều cao của hình lăng trụ là bao nhiêu?

b) Hãy tạo lập hình lăng trụ đứng tam giác này.

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

a) Sử dụng tính chất của cạnh hình lăng trụ suy ra chiều cao

b) Gấp theo đường nét đứt

Lời giải chi tiết

a) Hình lăng trụ đứng tam giác có các mặt bên là hình chữ nhật và hai đáy là hình tam giác.

Do đó, chiều cao của hình lăng trụ là 70 cm.

b) – Trên tấm bìa vẽ hình chữ nhật và hai hình tam giác vuông như hình dưới đây.

– Gấp theo đường nét đứt ta được hình lăng trụ đứng tam giác.

–>

— *****

Giải bài 6 trang 60 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

Hãy chỉ ra cách cắt một chiếc hộp hình chữ nhật thành hai hình lăng trụ đứng có đáy là hình thang.

Hướng dẫn giải chi tiết Bài 6

Phương pháp giải

Sử dụng tính chất, dấu hiệu nhận biết của hình lăng trụ đứng

Lời giải chi tiết

Cho hình hộp chữ nhật ABCD.EFGH.

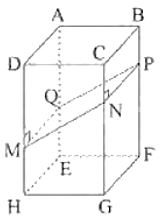
– Trên đoạn DH và CG, lấy hai điểm M, N, sao cho MN không vuông góc với CG như hình trên.

– Kẻ đoạn thẳng NP vuông góc với CG, và MQ vuông góc với DH.

– Cắt theo các cạnh MN, NP, PQ, QM, ta được 2 hình lăng trụ đứng thỏa mãn yêu cầu.

–>

— *****