Giải bài 4.44 trang 69 SBT Toán 7 – KN

Giải bài 4.44 trang 69 SBT Toán 7 – KN – SÁCH BÀI TẬP TOÁN 7 – KẾT NỐI TRI THỨC
THUỘC BÀI SỐ: Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng- ..

=======

Đề bài

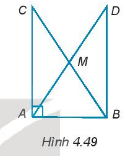
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:

a)\(\Delta ABD\) vuông tại B.

b)\(\Delta ABD = \Delta BAC\)

c) Các tam giác AMB, AMC là các tam giác cân tại đỉnh M.

Phương pháp giải –

a)Chứng minh:\(\Delta AMC = \Delta DMB\left( {c – g – c} \right)\)

b)Dựa vào ý a suy ra BD = CA

c)

-Chứng minh: \(\widehat {BDA} = \widehat {CAD}\left( {AC\parallel BD} \right)\)

-Chứng minh các góc ở đáy bằng nhau.

Lời giải chi tiết

a)

Xét \(\Delta AMC\)và \(\Delta DMB\) có

MA = MD

MC = MB

\(\widehat {AMC} = \widehat {DMB}\)(2 góc đối đỉnh)

\(\begin{array}{l} \Rightarrow \Delta AMC = \Delta DMB\left( {c – g – c} \right)\\ \Rightarrow \widehat {DBM} = \widehat {MCA}\end{array}\)

Ta có:

\(\widehat {ABD} = \widehat {ABM} + \widehat {DBM} = \widehat {ABC} + \widehat {BCA} = {90^0}\)

Vậy tam giác ABD vuông tại B.

b)

Xét \(\Delta ABD\) và \(\Delta BAC\) có:

\(\begin{array}{l}\widehat {ABD} = \widehat {BAC} = {90^0}\\BD = CA\left( {do\,\Delta AMC = \Delta DMB} \right)\end{array}\)

AB: Cạnh chung

\( \Rightarrow \Delta ABD = \Delta BAC\left( {c – g – c} \right)\)

c)

Ta có: \(\Delta ABD = \Delta BAC\left( {cmt} \right) \Rightarrow \widehat {ACB} = \widehat {BDA}\)

Mặt khác: \(AC\parallel BD\)(vì cùng vuông góc với AB) nên \(\widehat {BDA} = \widehat {CAD}\)(2 góc so le trong)

Vì vậy ta có: \(\widehat {MCA} = \widehat {ACB} = \widehat {CAD} = \widehat {CAM}\)

Do đó tam giác AMC cân tại đỉnh M.

Vì M là trung điểm của BC nên MB = MC = MA

Do đó tam giác AMB cân tại đỉnh M. 

============

Thuộc chủ đề: Giải sách bài tập toán 7 – Kết nối