Giải bài tập Bài 6. Số vô tỉ. Căn bậc hai số học (C2 Toán 7 Kết nối)

Giải bài tập Bài 6. Số vô tỉ. Căn bậc hai số học (C2 Toán 7 Kết nối)

---

Giải bài 2.6 trang 32 SGK Toán 7 KNTT tập 1

Cho biết \({153^2} = 23409\). Hãy tính \(\sqrt {23409} \)

Phương pháp giải

\({x^2} = a\) thì \(\sqrt a  = x\) (x > 0)

Lời giải chi tiết

Do 153² = 23409 và 153 > 0 nên \(\sqrt {23409}  = 153.\)

Giải bài 2.7 trang 32 SGK Toán 7 KNTT tập 1

Từ các số là bình phương cảu 12 số tự nhiên đầu tiên, em hãy tìm căn bậc hai số học của các số sau:

a) 9;

b) 16;

c) 81;

d) 121

Phương pháp giải

\({x^2} = a\) thì \(\sqrt a  = x\) (x > 0)

Lời giải chi tiết

a) Vì \({3^2} = 9\) nên \(\sqrt 9  = 3\)

b) Vì \({4^2} = 16\) nên \(\sqrt {16}  = 4\)

c) Vì \({9^2} = 81\) nên \(\sqrt {81}  = 9\)

d) Vì \({11^2} = 121\) nên \(\sqrt {121}  = 11\)

Giải bài 2.8 trang 32 SGK Toán 7 KNTT tập 1

Khi tìm căn bậc hai số học của một số tự nhiên ta thường phân tích số đó ra thừa số nguyên tố. Chẳng hạn:

Vì \(324 = {2^2}{.3^4} = {({2.3^2})^2} = {18^2}\) nên \(\sqrt {324}  = 18\)

Tính căn bậc hai số học của 129 600.

Phương pháp giải

Phân tích 129 600 ra thừa số nguyên tố, rồi đưa về dạng \({a^2}\)

Lời giải chi tiết

Ta có: 129600 = 2⁶ . 3⁴ . 5² = \({\left( {{2^3}{{.3}^2}.5} \right)^2}\) = 360² nên \(\sqrt {129600}  = 360.\)

 

Giải bài 2.9 trang 32 SGK Toán 7 KNTT tập 1

Tính độ dài các cạnh của hình vuông có diện tích bằng:

a) 81 dm²;

b) 3 600 m²;

c) 1 ha

Phương pháp giải

Tìm căn bậc hai số học của một số.

Chú ý đơn vị.

Lời giải chi tiết

a) Độ dài các cạnh của hình vuông là: \(\sqrt {81}  = 9\) (dm)

b) Độ dài các cạnh của hình vuông là: \(\sqrt {3600}  = 60\) (m)

c) Đổi 1 ha  = 10 000 m²

Độ dài các cạnh của hình vuông là: \(\sqrt {10000}  = 100\) (m)

Chú ý:  Câu c cần đổi đơn vị trước khi tìm căn bậc hai số học.

Giải bài 2.10 trang 32 SGK Toán 7 KNTT tập 1

Sử dụng máy tính cầm tay tìm căn bậc hai số học của các số sau rồi làm tròn các kết quả với độ chính xác 0,005.

a) 3;

b) 41;

c) 2 021

Phương pháp giải

* Bấm máy tính tìm căn bậc hai số học.

* Làm tròn theo quy tắc làm tròn số thập phân.

– Đối với chữ số hàng làm tròn:

+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;

+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5

– Đối với chữ số sau hàng làm tròn:

+ Bỏ đi nếu ở phần thập phân;

+ Thay bằng các chữ số 0 nếu ở phần số nguyên

Lời giải chi tiết

Làm tròn các kết quả với độ chính xác 0,005 tức là làm tròn đến hàng phần trăm.

\(\begin{array}{l}a)\sqrt 3  = 1,73205…. \approx 1,73\\b)\sqrt {41}  = 6,40312…. \approx 6,40\\c)\sqrt {2021}  = 44,95553…. \approx 44,96\end{array}\)

Giải bài 2.11 trang 32 SGK Toán 7 KNTT tập 1

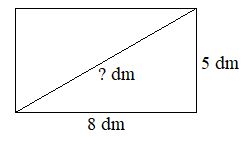
Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 8 dm và chiều rộng là 5 dm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu đềximét (làm tròn kết quả đến hàng phần mười)?

Phương pháp giải

Bước 1: Tính tổng các bình phương độ dài hai cạnh của hình chữ nhật.

Bước 2: Tìm căn bậc hai số học của tổng vừa tìm được bằng máy tính cầm tay

Bước 3: Làm tròn kết quả đến hàng phần mười.

Lời giải chi tiết

Ta có: Bình phương độ dài đường chéo của một hình chữ nhật là: \({5^2} + {8^2} = 25 + 64 = 89\)

Độ dài đường chéo của một hình chữ nhật là: \(\sqrt {89}  = 9,43398…\)(dm)

Làm tròn kết quả này ta được: 9,4 dm

Chú ý:  Độ dài đường chéo của một hình chữ nhật bằng căn bậc hai số học của tổng các bình phương độ dài hai cạnh của nó

Giải bài 2.12 trang 32 SGK Toán 7 KNTT tập 1

Để lát một mảnh sân hình vuông có diện tích 100 m², người ta cần dùng bao nhiêu viên gạch hình vuông có cạnh dài 50 cm (coi các mạch ghép là không đáng kể)?

Phương pháp giải

Bước 1: Tìm diện tích 1 viên gạch

Bước 2: Đổi các số liệu về cùng đơn vị

Bước 3: Tìm số viên gạch

Lời giải chi tiết

Diện tích một viên gạch là: 50² = 2500 (cm²)

Đổi 2500 cm² = 0,25 m².

Người ta cần số viên gạch là: 100 : 0,25 = 400 (viên).

Vậy người ta cần dùng 400 viên gạch để lát sân.