Lý thuyết Bài 3: Các phép toán trên tập hợp – Chân trời
============
Tóm tắt lý thuyết
1.1. Hợp và giao của các tập hợp
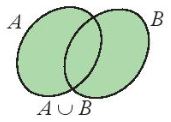
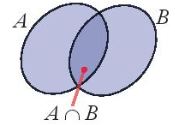
| Cho hai tập hợp A và B. – Tập hợp các phần tử thuộc A hoặc thuộc B gọi là hợp của hai tập hợp A và B, kí hiệu \(A \cup B\). \(A \cup B = {\rm{\{ }}x|x \in A\) hoặc \(x \in B{\rm{\} }}\) – Tập hợp các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B, kí hiệu \(A \cap B\). \(A \cap B = {\rm{\{ }}x|x \in A\) và \(x \in B{\rm{\} }}\) |
|---|
Ví dụ: Xác định \(A \cup B\) và \(A \cap B\) trong mỗi trường hợp sau:
a) A= {2; 3; 5; 7}, B={1; 3, 5; 15};
b) \(A = \left\{ {x \in R|x(x + 2) = 0} \right\},B = \left\{ {x \in R|{x^2} + 2 = 0} \right\}\)
c) A là tập hợp các hình bình hành, B là tập hợp các hình thoi.
Giải
a) 4\(A \cup B\) = (1;2;3;5; 7; 15), \(A \cap B\) = (3; 5}
b) Phương trình x(x + 2) = 0 có hai nghiệm là 0 và -2. nên A = {-2; 0}
Phương trình \({x^2} + 2 = 0\) vô nghiệm, nên B = Ø
Từ đó \(A \cup B = A \cup \emptyset {\rm{ }} = A = \left\{ { – 2;0} \right\},A \cap B = A \cap {\rm{ }}\emptyset {\rm{ }} = {\rm{ }}\emptyset {\rm{ }}\)
e) Vì mỗi hình thoi cũng là hình bình hành nên \(B \subset A\). Từ đó, \(A \cup B = A,A \cap B = B\)
Nhận xét:
- Nếu A và B là hai tập hợp hữu hạn thì \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) – n\left( {A \cap B} \right)\)
- Đặc biệt, nếu A và B không có phần tử chung, tức \(A \cap B = \emptyset \) \) thì \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right)\)
1.2. Hiệu của hai tập hợp, phần bù của tập con
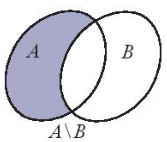
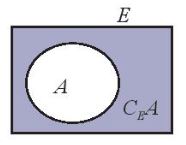
| Cho hai tập hợp A và B. – Tâp hợp các phần tử thuộc A nhưng không thuộc B gọi là liệu của A và B, kí hiệu \(A\backslash B\) \(A\backslash B = {\rm{\{ }}x|x \in A\) và \(x \notin B{\rm{\} }}\). – Nếu A là tập con của E thì hiệu \(E\backslash A\) gọi là phân bù của A trong E, kí hiệu \({C_E}A\). |
|---|
Ví dụ: Cho E = {x \(\in\) N | x < 10}, A = {0; 2′ 4; 6; 8}, B = {0; 3; 6; 9}
Xác định các tập hợp \(A\backslash B,B\backslash A,{C_E}A,{C_E}B\).
Giải
Ta có: \(A\backslash B = \left\{ {2;4;8} \right\},B\backslash A = \left\{ {3;9} \right\},{C_E}A = \left\{ {1;3;5;7;9} \right\},{C_E}B = \left\{ {1;2;4;5;7;8} \right\}\)
Chú ý: Trong các chương sau, để tìm các tập hợp là hợp, giao, hiệu, phần bù của những tập con của tập số thực, ta thường vẽ sơ đồ trên trục số.
Bài tập minh họa
Câu 1: Cho \(A = \{ (x;y)|x,y \in \mathbb{R},3x – y = 9\} \), \(B = \{ (x;y)|\;x,y \in \mathbb{R},x – y = 1\} \)
Hãy xác định \(A \cap B\).
Hướng dẫn giải
\(A \cap B = \{ (x;y)|\;x,y \in \mathbb{R},3x – y = 9,x – y = 1\} \)
Tức là \(A \cap B\)là tập hợp các cặp số (x;y) thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}3x – y = 9\\x – y = 1\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}y = 3x – 9\\y = x – 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x – 1 = 3x – 9\\y = x – 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2x = 8\\y = x – 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right.\end{array}\)
Vậy \(A \cap B = \{ (4;3)\} .\)
Câu 2: Cho tập hợp \(E = \{ x \in \mathbb{N}|x < 8\} ,A = \{ 0;1;2;3;4\} ,B = \{ 3;4;5\} \)
Xác định các tập hợp sau đây:
a) A\B, B\A và \((A\backslash B) \cap {\rm{(}}B\backslash A)\)
b) \({C_E}(A \cap B)\) và \(({C_E}A) \cap ({C_E}B)\)
c) \({C_E}(A \cup B)\) và \(({C_E}A) \cup ({C_E}B)\)
Hướng dẫn giải
\(E = \{ x \in \mathbb{N}|x < 8\} = \{ 0;1;2;3;4;5;6;7\} \)
a) Ta có: \(A\backslash B = \left\{ {0;1;2} \right\}\), \(B\backslash A = \left\{ 5 \right\},\)\((A\backslash B) \cap {\rm{(}}B\backslash A) = \emptyset \)
b) Ta có: \(A \cap B = \{ 3;4\} ,\;{C_E}(A \cap B) = \{ 0;1;2;5;6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cap ({C_E}B) = \{ 6;7\} \)
c) Ta có: \(A \cup B = \{ 0;1;2;3;4;5\} ,\;{C_E}(A \cup B) = \{ 6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cup ({C_E}B) = \{ 0;1;2;5;6;7\} \)
Luyện tập Bài 3 Chương 1 Toán 10 CTST
Qua bài giảng Các phép toán trên tập hợp này giúp các em nắm được các nội dung như sau:
– Nắm vững các khái niệm hợp, giao, hiệu, phần bù của hai tập hợp.
– Biết cách xác định hợp, giao, hiệu, phần bù của hai tập hợp.
===========
Chuyên mục: Học Toán lớp 10 – Chân trời
