Giải SBT Toán 6 tập 2 bài 4: Phép nhân, phép chia phân số – Cánh diều

Giải SBT Toán 6 tập 2 bài 4: Phép nhân, phép chia phân số – SBT CÁNH DIỀU

============
Chuyên mục: Giải sách bài tập toán 6 – SBT CÁNH DIỀU
=============

Câu 38. Tính tích và viết kết quả ở dạng phân số tối giản:

a) $frac{-4}{7}$.$frac{7}{-16}$

b) $frac{5}{-11}$.22

c) $frac{-5}{16}$.(-32)

d) 35.$frac{-4}{21}$

e) $frac{25}{10}$.1$frac{1}{3}$

g) $frac{-37}{401}$.(-1)

h) (1 – $frac{-1}{5}$).($frac{-3}{10}$ + $frac{1}{5}$)

i) $frac{-3}{5}$.$frac{-3}{5}$.$frac{1}{3}$

Trả lời:

a) $frac{-4}{7}$.$frac{7}{-16}$ = $frac{1}{4}$

b) $frac{5}{-11}$.22 = -10

c) $frac{-5}{16}$.(-32) = 10

d) 35.$frac{-4}{21}$ = $frac{-20}{3}$

e) $frac{25}{10}$.1$frac{1}{3}$ = $frac{10}{3}$

g) $frac{-37}{401}$.(-1) = $frac{37}{401}$

h) (1 – $frac{-1}{5}$).($frac{-3}{10}$ + $frac{1}{5}$) = $frac{-2}{25}$

i) $frac{-3}{5}$.$frac{-3}{5}$.$frac{1}{3}$ = $frac{3}{25}$

Câu 39. Thực hiện các phép tính sau:

a) $frac{5}{12}$ + $frac{21}{8}$.$frac{1}{14}$

b) $frac{8}{15}$.$frac{3}{64}$ – $frac{13}{25}$

c) ($frac{19}{21}$ – $frac{2}{3}$).$frac{28}{10}$

d) (1 – $frac{5}{17}$).($frac{3}{8}$ – $frac{5^{2}}{24}$)

Trả lời:

a) $frac{5}{12}$ + $frac{21}{8}$.$frac{1}{14}$ = $frac{5}{12}$ + $frac{3}{16}$ = $frac{29}{48}$

b) $frac{8}{15}$.$frac{3}{64}$ – $frac{13}{25}$ = $frac{1}{40}$ – $frac{13}{25}$ = $frac{-99}{200}$

c) ($frac{19}{21}$ – $frac{2}{3}$).$frac{28}{10}$ = $frac{5}{21}$.$frac{14}{5}$ = $frac{2}{3}$

d) (1 – $frac{5}{17}$).($frac{3}{8}$ – $frac{5^{2}}{24}$) = $frac{12}{17}$.$frac{-16}{24}$ = $frac{-8}{17}$

Câu 40. Tính một cách hợp lí:

a) $frac{11}{4}$.$frac{-5}{9}$.$frac{8}{33}$

b) $frac{-5}{6}$.$frac{4}{19}$ + $frac{-7}{12}$.$frac{4}{19}$ – $frac{40}{57}$

c) ($frac{23}{41}$ – $frac{15}{82}$).$frac{41}{15}$

d) 9.($frac{151515}{171717}$ – $frac{131313}{181818}$)

e) $frac{-13}{8}$.($frac{8}{13}$ + $frac{32}{28}$) – $frac{15}{7}$

g) $frac{2^{2}}{1.3}$.$frac{3^{2}}{2.4}$.$frac{4^{2}}{3.5}$.$frac{5^{2}}{4.6}$.$frac{6^{2}}{5.7}$

Trả lời:

a) $frac{11}{4}$.$frac{-5}{9}$.$frac{8}{33}$ = $frac{11.(-5).2.4}{4.9.3.11}$ = $frac{-10}{27}$

b) $frac{-5}{6}$.$frac{4}{19}$ + $frac{-7}{12}$.$frac{4}{19}$ – $frac{40}{57}$ = $frac{4}{19}$.($frac{-5}{6}$ + $frac{-7}{12}$) – $frac{40}{57}$ = $frac{-17}{57}$ + $frac{-40}{57}$ = -1

c) ($frac{23}{41}$ – $frac{15}{82}$).$frac{41}{15}$ = $frac{23}{41}$.$frac{41}{15}$ – $frac{15}{82}$.$frac{41}{15}$ = $frac{23}{15}$ – $frac{1}{2}$ = $frac{31}{30}$

d) 9.($frac{151515}{171717}$ – $frac{131313}{181818}$) = 9.($frac{15}{17}$ – $frac{13}{18}$) = 9.$frac{49}{306}$ = $frac{49}{34}$

e) $frac{-13}{8}$.($frac{8}{13}$ + $frac{32}{28}$) – $frac{15}{7}$

= $frac{-13}{8}$.($frac{8}{13}$ + $frac{8}{7}$) – $frac{15}{7}$

= $frac{-13}{8}$.$frac{8}{13}$ – $frac{13}{8}$.$frac{8}{7}$ – $frac{15}{7}$

= (-1) – $frac{13}{7}$ – $frac{15}{7}$ = -5

g) $frac{2^{2}}{1.3}$.$frac{3^{2}}{2.4}$.$frac{4^{2}}{3.5}$.$frac{5^{2}}{4.6}$.$frac{6^{2}}{5.7}$

= $frac{2.3.4.5.6}{1.2.3.4.5}$.$frac{2.3.4.5.6}{3.4.5.6.7}$ = $frac{6}{1}$.$frac{2}{7}$ = $frac{12}{7}$

Câu 41. Tìm số nguyên thích hợp cho chỗ chấm.

a) $frac{7}{25}$.$frac{…}{28}$ = $frac{-3}{20}$

b) $frac{46}{15}$.$frac{-3}{…}$ = $frac{23}{5}$

c) $frac{…}{-18}$.$frac{5}{2}$ = $frac{-5}{12}$

Trả lời:

Ta điền các số như sau:

a) $frac{7}{25}$.$frac{-15}{28}$ = $frac{-3}{20}$

b) $frac{46}{15}$.$frac{-3}{-2}$ = $frac{23}{5}$

c) $frac{3}{-18}$.$frac{5}{2}$ = $frac{-5}{12}$

Câu 42. Một chiếc xe máy tự động kiểm tra linh kiện điện tử cứ $frac{16}{25}$ giây thì kiểm tra được 1 linh kiện. Trong 1 giờ máy tự động kiểm tra được bao nhiêu linh kiện điện từ?

Trả lời:

Ta có: 1 giờ = 3600 giây

Do đó trong 1 giờ máy tự động kiểm tra được số linh kiện là:

3600.$frac{16}{25}$ = 5625 (linh kiện)

Đáp số: 5625 linh kiện

Câu 43. Em hãy tính các tích sau rồi viết chữ vào các ô trống tương ứng với đáp số đúng. Khi đó em sẽ biết được tên của một phố cổ ở Hà Nội.

Ê. $frac{2}{7}$.$frac{14}{5}$.$frac{-1}{3}$

N. $frac{-15}{16}$.$frac{8}{-25}$

G. $frac{-5}{13}$.26

U. $(frac{3}{8})^{2}$

C. (2 – $frac{1}{2}$).($frac{-3}{4}$ – $frac{1}{2}$)

À. $frac{7}{11}$.$frac{-1}{7}$.$frac{11}{9}$.0

H. 18.$frac{3}{10}$.(-5)

I. $frac{15}{-49}$.$frac{-84}{35}$

-27	0	$frac{3}{10}$	-10	$frac{-15}{8}$	-27	$frac{36}{49}$	$frac{-4}{15}$	$frac{9}{64}$

Trả lời:

Ê. $frac{2}{7}$.$frac{14}{5}$.$frac{-1}{3}$ = $frac{-4}{15}$

N. $frac{-15}{16}$.$frac{8}{-25}$ = $frac{3}{10}$

G. $frac{-5}{13}$.26 = -10

U. $(frac{3}{8})^{2}$ = $frac{9}{64}$

C. (2 – $frac{1}{2}$).($frac{-3}{4}$ – $frac{1}{2}$) = $frac{-15}{8}$

À. $frac{7}{11}$.$frac{-1}{7}$.$frac{11}{9}$.0 = 0

H. 18.$frac{3}{10}$.(-5) = -27

I. $frac{15}{-49}$.$frac{-84}{35}$ = $frac{36}{49}$

H	À	N	G	C	H	I	Ế	U
-27	0	$frac{3}{10}$	-10	$frac{-15}{8}$	-27	$frac{36}{49}$	$frac{-4}{15}$	$frac{9}{64}$

Câu 44. Tìm số nguyên âm lớn nhất để khi nhân nó với một trong các phân số tối giản sau đều được tích là những số nguyên: $frac{5}{6}$; $frac{-7}{15}$; $frac{11}{21}$

b) Tìm số tự nhiên a nhỏ nhất sao cho khi lấy a chia cho $frac{8}{9}$ hoặc $frac{17}{12}$, ta đều được kết quả là số tự nhiên.

Trả lời:

a) Gọi a là số nguyên dương nhỏ nhất mà khi nó nhân với $frac{5}{6}$; $frac{-7}{15}$; $frac{11}{21}$ đều được tích là những số nguyên.

Để $frac{5a}{6}$; $frac{-7a}{15}$; $frac{11a}{21}$ là các số nguyên thì a phải chia hết cho 6; 15; 21 (do ƯCLN(5, 6) = 1; ƯCLN(-7, 15) = 1; ƯCLN(11, 21) = 1)

Mà a là số nguyên dương nhỏ nhất nên a = BCNN(6, 15, 21) = 210

Vậy số a cần tìm là 210

b) Ta có:

a : $frac{8}{9}$ = a.$frac{9}{8}$ = $frac{9a}{8}$ là số tự nhiên suy ra 9a chia hết cho 8.

Mà ƯCLN(9, 8) = 1 nên a chia hết cho 8

a : $frac{12}{17}$ = a.$frac{17}{12}$ = $frac{917a}{12}$ là số tự nhiên suy ra 17a chia hết cho 12.

Mà ƯCLN(12, 17) = 1 nên a chia hết cho 12

Mà a nhỏ nhất nên a = BCNN(8, 12) = 24

Câu 45. So sánh:

A = $frac{3^{2}}{2.5}$ + $frac{3^{2}}{5.8}$ + $frac{3^{2}}{8.11}$ và B = $frac{4}{5.7}$ + $frac{4}{7.9}$ + … + $frac{4}{59.61}$

Trả lời:

A = $frac{3^{2}}{2.5}$ + $frac{3^{2}}{5.8}$ + $frac{3^{2}}{8.11}$

   = 3.($frac{3}{2.5}$ + $frac{3}{5.8}$ + $frac{3}{8.11}$)

   = 3.($frac{1}{2}$ – $frac{1}{5}$ + $frac{1}{5}$ – $frac{1}{8}$ + $frac{1}{8}$ – $frac{1}{11}$)

   = 3.($frac{1}{2}$ – $frac{1}{11}$) = $frac{27}{22}$

B = $frac{4}{5.7}$ + $frac{4}{7.9}$ + … + $frac{4}{59.61}$

   = $frac{2}{5}$ – $frac{2}{7}$ + $frac{2}{7}$ – $frac{2}{9}$ + … + $frac{2}{59}$ – $frac{2}{61}$

   = $frac{2}{5}$ – $frac{2}{61}$

   = $frac{112}{305}$ 

Ta thấy A > 1 > B

Vậy A > B

Câu 46. Tìm các tích sau:

a) 1$frac{1}{2}$.1$frac{1}{3}$.1$frac{1}{4}$.1$frac{1}{5}$.1$frac{1}{6}$.1$frac{1}{7}$

b) (1 – $frac{1}{2}$)(1 – $frac{1}{3}$)(1 – $frac{1}{4}$) … (1 – $frac{1}{50}$)

Trả lời:

a) 1$frac{1}{2}$.1$frac{1}{3}$.1$frac{1}{4}$.1$frac{1}{5}$.1$frac{1}{6}$.1$frac{1}{7}$

= $frac{3}{2}$.$frac{4}{3}$.$frac{5}{4}$.$frac{6}{5}$.$frac{7}{6}$.$frac{8}{7}$

= 4

b) (1 – $frac{1}{2}$)(1 – $frac{1}{3}$)(1 – $frac{1}{4}$) … (1 – $frac{1}{50}$)

= $frac{1}{2}$.$frac{2}{3}$.$frac{3}{4}$…$frac{49}{50}$

= $frac{1}{50}$

Câu 47. Tìm số thích hợp điền vào chỗ chấm (…) trong mỗi hình sau:

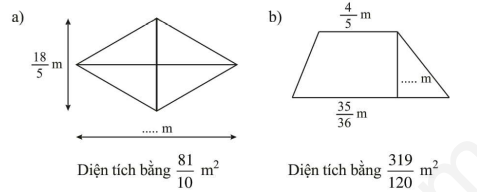
Trả lời:

Áp dụng công thức tính diện tích các hình đa giác ta được:

a) $frac{9}{2}$ m

b) 3 m

Câu 48. Một ca nô xuôi dòng trên khúc sông AB hết 6 giờ và ngược dòng trên khúc sông BA hết 8 giờ. Hãy tính chiều dài khúc sông đó, biết vận tốc dòng nước là 50 m/min

Trả lời:

Đổi : 50 m/min = 3km/h

Trong một giờ ca nô xuôi dòng đi được: 1: 6 = $frac{1}{6}$ (khúc sông AB)

Trong một giờ ca nô ngược dòng đi được: 1 : 8 = $frac{1}{8}$ (khúc sông BA)

Trong một giờ dòng nước chảy được là: ($frac{1}{6}$ – $frac{1}{8}$) : 2 = $frac{1}{48}$ (khúc sông AB)

Thời gian dòng nước xuôi từ A đến B là: 1 : $frac{1}{48}$ = 48 (giờ)

Khúc sông AB dài là: 3.48 = 144 (km)

Câu 49. Tìm x, biết:

a) $frac{6}{7}$.x = $frac{18}{23}$

b) $frac{15}{119}$.x = 1

c) x : $frac{5}{6}$ = $frac{4}{7}$

d) x – $frac{3}{7}$ : $frac{9}{14}$ = $frac{-7}{3}$

e) $frac{9}{13}$.x = $frac{11}{8}$ – $frac{125}{1000}$

g) (x – $frac{1}{2}$) : $frac{3}{11}$ = $frac{11}{4}$

Trả lời:

a) x = $frac{18}{23}$ : $frac{6}{7}$ = $frac{18}{23}$.$frac{7}{6}$ = $frac{21}{23}$

b) x = 1 : $frac{15}{119}$ = $frac{119}{15}$

c) x = $frac{4}{7}$.$frac{5}{6}$ = $frac{15}{119}$

d) x = $frac{-5}{3}$

e) x = $frac{65}{36}$

g) x = $frac{5}{4}$

Câu 50. Tính:

a) $frac{frac{3}{5}+frac{3}{27}-frac{3}{9}-frac{3}{11}}{frac{4}{5}+frac{4}{27}-frac{4}{9}-frac{4}{11}}$

b) $frac{5-frac{5}{3}-frac{5}{27}}{8-frac{8}{3}-frac{8}{27}} : frac{15+frac{15}{121}-frac{15}{11}}{16+frac{16}{121}-frac{16}{11}}$

c) $frac{1}{2}:left ( frac{-3}{2} right ):frac{4}{3}:left ( frac{-5}{4} right ):frac{6}{5}:left ( frac{-7}{6} right ):…:left ( frac{-101}{100} right )$

Trả lời:

a) $frac{frac{3}{5}+frac{3}{27}-frac{3}{9}-frac{3}{11}}{frac{4}{5}+frac{4}{27}-frac{4}{9}-frac{4}{11}}$ 

 = $frac{3.(frac{3}{5}+frac{3}{27}-frac{3}{9}-frac{3}{11})}{4.(frac{4}{5}+frac{4}{27}-frac{4}{9}-frac{4}{11})}$

 = $frac{3}{4}$

b) $frac{5-frac{5}{3}-frac{5}{27}}{8-frac{8}{3}-frac{8}{27}} : frac{15+frac{15}{121}-frac{15}{11}}{16+frac{16}{121}-frac{16}{11}}$ = $frac{2}{3}$

c) $frac{1}{2}:left ( frac{-3}{2} right ):frac{4}{3}:left ( frac{-5}{4} right ):frac{6}{5}:left ( frac{-7}{6} right ):…:left ( frac{-101}{100} right )$ = $frac{1}{101}$

Câu 51. Hai bạn Ngọc và Hà có tổng số tiền là 76000 đồng. Biết $frac{3}{5}$ số tiền của Ngọc bằng $frac{2}{3}$ số tiền của Hà. Mỗi bạn có bao nhiêu tiền?

Trả lời:

Gọi số tiền của Ngọc là a (đồng; a > 0)

$frac{3}{5}$ số tiền của Ngọc là $frac{3a}{5}$ số tiền của Ngọc

$frac{3}{5}$ số tiền của Ngọc bằng $frac{2}{3}$ số tiền của Hà nên $frac{2}{3}$ số tiền của Hà là $frac{3a}{5}$

Do đó số tiền của Hà là $frac{3a}{5}$.$frac{3}{2}$ = $frac{9a}{10}$

Tổng số tiền của hai bạn là 76000 đồng nên:

a + $frac{9a}{10}$ = 76000 = $frac{19a}{10}$

Suy ra a = 40000 (đồng)

Vậy số tiền của Ngọc là 40000 đồng, số tiền của Hà là 36000 đồng.

Câu 52. Bây giờ là 12 giờ (Hình 4). Sau ít nhất bao nhiêu phút nữa thì kim giờ và kim phút vuông góc với nhau?

Trả lời:

Lúc 12 giờ hai kim đồng hồ trùng nhau.

Để hai kim đồng hồ vuông góc với nhau thì kim phút phải vượt kim giờ $frac{1}{4}$ vòng.

Thời gian ngắn nhất để hai kim đồng hồ vuông góc với nhau là:

$frac{1}{4}$ : (1 – $frac{1}{12}$) = $frac{3}{11}$ (giờ) = $frac{180}{11}$ (phút)

======
Thẻ Chương [Sách cánh diều] Giải SBT Toán 6 – Giải SBT Toán 6 tập 2 cánh diều