Lý thuyết Bài Giá trị lượng giác của một góc bất kỳ từ 0 đến 180 độ

Lý thuyết Bài Giá trị lượng giác của một góc bất kỳ từ 0 đến 180 độ

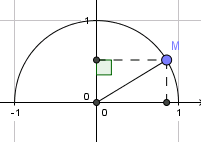
Trước khi đi vào định nghĩa, ta xét hình sau:

Hình trên mô phỏng một nửa đường tròn có bán kín bằng 1. Ta gọi nó là  nửa đường tròn đơn vị .

Điểm M thuộc nửa đường tròn ấy, vậy góc cho trước có độ lớn từ 0 độ đến 180 độ.

1. Định nghĩa

Với mỗi góc \(\alpha(0^o\leq \alpha\leq 180^o)\), ta xác định điểm M trên nửa đường tròn sao cho \(\widehat{MOx}=\alpha\). Giả sử điểm M(x;y). Khi đó:

Tung độ y của điểm M được gọi là sin của góc \(\alpha\), ta kí hiệu là \(sin\alpha\)

Hoành độ x của điểm M được gọi là cosin của góc \(\alpha\), ta kí hiệu là \(cos\alpha\).

Tỉ số  \(\frac{y}{x}\) \((x\neq 0)\) được gọi là tan của góc \(\alpha\), ta kí hiệu là \(tan\alpha\)

Tỉ số  \(\frac{x}{y}\) \((y\neq 0)\) được gọi là côtan của góc \(\alpha\), ta kí hiệu là \(cot\alpha\)

Chú ý : Từ định nghĩa ta có:
+ Gọi $P$, $Q$ lần lượt là hình chiếu của $M$ lên trục $Ox$, $Oy$ khi đó $M(\overline {OP} ;\overline {OQ} ).$
+ Với ${0^0} \le \alpha \le {180^0}$ ta có $0 \le \sin \alpha \le 1$, $ – 1 \le \cos \alpha \le 1.$
+ Dấu của giá trị lượng giác:

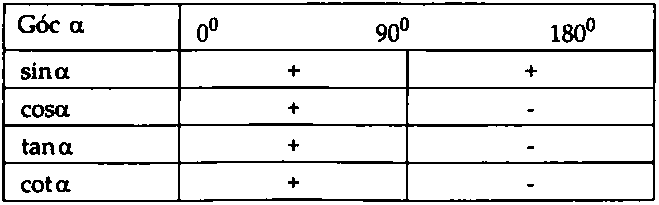
2. Tính chất quan trọng:

Nếu hai góc bù nhau thì sin của chúng bằng nhau, còn cos, tan và cot của chúng đối nhau, cụ thể là:

• \(sin(180^o-\alpha)=sin\alpha\)
• \(cos(180^o-\alpha)=-cos\alpha\)
• \(tan(180^o-\alpha)=-tan\alpha(\alpha\neq 90^o)\)
• \(cot(180^o-\alpha)=-cot\alpha(0^o<\alpha<180^o)\)

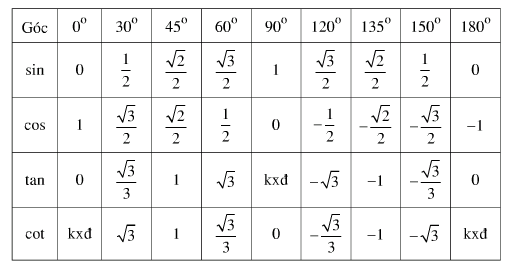
3. Giá trị lượng giác của các góc đặc biệt

4. Các hệ thức lượng giác cơ bản

1) $\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}$ $\left( {\alpha \ne {{90}^0}} \right).$
2) $\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}$ $\left( {\alpha \ne {0^0};{{180}^0}} \right).$
3) $\tan \alpha .\cot \alpha = 1$ $\left( {\alpha \ne {0^0};{{90}^0};{{180}^0}} \right).$
4) ${\sin ^2}\alpha + {\cos ^2}\alpha = 1.$
5) $1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}$ $\left( {\alpha \ne {{90}^0}} \right).$
6) $1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}$ $\left( {\alpha \ne {0^0};{{180}^0}} \right).$
Chứng minh:
Hệ thức 1, 2 và 3 dễ dàng suy ra từ định nghĩa.
Ta có $\sin \alpha = \overline {OQ} $, $\cos \alpha = \overline {OP} .$
Suy ra ${\sin ^2}\alpha + {\cos ^2}\alpha $ $ = {\overline {OQ} ^2} + {\overline {OP} ^2}$ $ = O{Q^2} + O{P^2}.$
+ Nếu $\alpha = {0^0}$, $\alpha = {90^0}$ hoặc $\alpha = {180^0}$ thì dễ dàng thấy ${\sin ^2}\alpha + {\cos ^2}\alpha = 1.$
+ Nếu $\alpha \ne {0^0}$, $\alpha \ne {90^0}$ và $\alpha \ne {180^0}$ khi đó theo định lý Pitago ta có:
${\sin ^2}\alpha + {\cos ^2}\alpha $ $ = O{Q^2} + O{P^2}$ $ = O{Q^2} + Q{M^2}$ $ = O{M^2} = 1.$
Vậy ta có ${\sin ^2}\alpha + {\cos ^2}\alpha = 1.$
Mặt khác $1 + {\tan ^2}\alpha $ $ = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}$ $ = \frac{{{{\cos }^2}\alpha + {{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}$ $ = \frac{1}{{{{\cos }^2}\alpha }}$ suy ra được hệ thức 5.
Tương tự $1 + {\cot ^2}\alpha $ $ = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}$ $ = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}$ $ = \frac{1}{{{{\sin }^2}\alpha }}$ suy ra được hệ thức 6.