Đề thi mẫu HK1 Toán lớp 8 – số 5

—-12—-

Đề bài

Câu 1 (2,0 điểm):

1) Rút gọn rồi tính giá trịbiểu thức: \((2x + y)(y – 2x) + 4{x^2}\) tại \(x =  – 2018\) và \(y = 10\).

2) Phân tích các đa thức sau thành nhân tử:

\(a)\,\,xy + 11x\\b)\,\,{x^2} + 4{y^2} + 4xy – 16\)

Câu 2 (2,0 điểm):

1)Tìm \(x\) biết:

\(a)\,\,2{x^2} – 6x = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,b)\,\,(x + 3)({x^2} – 3x + 9) – x({x^2} – 2) = 15\)

2) Tìm số nguyên \(a\) sao cho \({x^3} + 3{x^2} – 8x + a – 2038\) chia hết cho \(x + 2\).

Câu 3 (2,0 điểm): Rút gọn các biểu thức sau:

\(\begin{array}{l}1)\,\,\dfrac{{6x + 4}}{{3x}}:\dfrac{{2y}}{{3x}}\\2)\,\,A = \left( {\dfrac{{x – 3}}{x} – \dfrac{x}{{x – 3}} + \dfrac{9}{{{x^2} – 3x}}} \right):\dfrac{{2x – 2}}{x}\end{array}\)

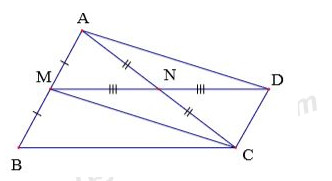
Câu 4 (3,0 điểm): Cho tam giác \(ABC,\,\,M,\,\,N\) lần lượt là trung điểm của \(AB\) và \(AC\). Gọi \(D\) là điểm đối xứng với điểm \(M\) qua điểm \(N\).

a) Tứ giác \(AMCD\) là hình gì? Vì sao?

Tìm điều kiện của tam giác \(ABC\) để tứ giác \(AMCD\) là hình chữ nhật.

b) Chứng minh tứ giác \(BCDM\) là hình bình hành.

Câu 5 (1,0 điểm):

a)  Cho \(x,y\) thỏa mãn \(2{x^2} + {y^2} + 9 = 6x + 2xy\). Tính giá trị của biểu thức \(A = {x^{2017}}{y^{2018}} – {x^{2018}}{y^{2017}} + \dfrac{1}{9}xy\).

b) Cho \(2\) số \(a\) và \(b\) thỏa mãn \(\dfrac{{a + b}}{2} = 1\).Tính giá trị lớn nhất của biểu thức: \(\dfrac{{2011}}{{2{a^2} + 2{b^2} + 2008}}\) .

Lời giải chi tiết

Câu 1:

1) \((2x + y)(y – 2x) + 4{x^2} = (y + 2x)(y – 2x) + 4{x^2} = {y^2} – 4{x^2} + 4{x^2} = {y^2}\)

Tại \(x =  – 2018\) và \(y = 10\) thay vào biểu thức ta được: \({10^2} = 100\).

Vậy giá trị của biểu thức \((2x + y)(y – 2x) + 4{x^2}\)với \(x =  – 2018\) và \(y = 10\)là \(100\).

2) Phân tích các đa thức sau thành nhân tử:

\(\begin{array}{l}a)\,\,xy + 11x\, = x.(y + 11)\\b)\,\,{x^2} + 4{y^2} + 4xy – 16 \\= \left( {{x^2} + 4xy + 4{y^2}} \right) – 16\\ = {(x + 2y)^2} – {4^2} = (x + 2y + 4)(x + 2y – 4)\end{array}\)

Câu 2:

1) Tìm x biết:

\(\begin{array}{l}a)\,\,2{x^2} – 6x = 0\,\,\,\,\,\,\,\,\,\,\,\,\\\, \Leftrightarrow \,2x(x – 3) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\,\, \Rightarrow \left[ \begin{array}{l}2x = 0\\x – 3 = 0\end{array} \right.\,\,\,\, \Rightarrow \left[ \begin{array}{l}x = 0\\x = 3\end{array} \right..\end{array}\)

Vậy \(x = 0\) hoặc \(x = 3\) .

\(\begin{array}{l}b)\,\,(x + 3)({x^2} – 3x + 9) – x({x^2} – 2) = 15\,\,\\ \Leftrightarrow {x^2} + 27 – {x^3} + 2x = 15\\ \Leftrightarrow 2x + 27 = 15\\ \Leftrightarrow 2x = 15 – 27\\ \Leftrightarrow \,2x =  – 12\\ \Leftrightarrow \,x =  – 12:2\\ \Leftrightarrow x =  – 6\end{array}\)

Vậy \(x =  – 6\).

2) Thực hiện phép chia \(({x^3} + 3{x^2} – 8x + a – 2038):(x + 2)\)ta có:

Suy ra để \({x^3} + 3{x^2} – 8x + a – 2038\) chia hết cho \(x + 2\) thì số dư phải bằng \(0\), hay \(a – 2018 = 0\,\, \to  \Rightarrow a = 2018\).

Câu 3:

\(1)\,\,\dfrac{{6x + 4}}{{3x}}:\dfrac{{2y}}{{3x}} = \dfrac{{6x + 4}}{{3x}} \cdot \dfrac{{3x}}{{2y}} = \dfrac{{(6x + 4).3x}}{{3x.2y}} = \dfrac{{6x + 4}}{{2y}}\)

\(\begin{array}{l}2)\,\,A = \left( {\dfrac{{x – 3}}{x} – \dfrac{x}{{x – 3}} + \dfrac{9}{{{x^2} – 3x}}} \right):\dfrac{{2x – 2}}{x}\\\,\,\,\,\,\,A = \left( {\dfrac{{{{(x – 3)}^2}}}{{x(x – 3)}} – \dfrac{{x.x}}{{x – 3}} + \dfrac{9}{{{x^2} – 3x}}} \right) \cdot \dfrac{x}{{2x – 2}}\\\,\,\,\,\,\,A = \left( {\dfrac{{{{(x – 3)}^2} – {x^2} + 9}}{{x(x – 3)}}} \right) \cdot \dfrac{x}{{2(x – 1)}}\\\,\,\,\,\,\,A = \dfrac{{{x^2} – 6x + 9 – {x^2} + 9}}{{x(x – 3)}} \cdot \dfrac{x}{{2(x – 1)}}\\\,\,\,\,\,A = \dfrac{{ – 6x + 18}}{{x(x – 3)}} \cdot \dfrac{x}{{2(x – 1)}} = \dfrac{{ – 6(x – 3)x}}{{x(x – 3).2.(x – 1)}} = \dfrac{{ – 3}}{{x – 1}}\end{array}\)

Câu 4:

a) Ta có: \(3\) điểm \(M,N,D\) thẳng hàng (vì \(D\) đối xứng với \(M\) qua \(N\))

\(AN = NC\,\,\,(gt)\)

\(MN = ND\)(vì \(D\) đối xứng với \(M\) qua \(N\))

Suy ra tứ giác \(AMCD\) có hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Vậy \(AMCD\) là hình bình hành. (dhnb)

Hình bình hành \(AMCD\) là hình chữ nhật

\( \Leftrightarrow \angle AMC = {90^0} \Leftrightarrow AB \bot CM \Leftrightarrow \Delta ABC\) cân tại \(C\). (tính chất)

Vậy \(AMCD\) là hình chữ nhật \( \Leftrightarrow \Delta ABC\)cân tại \(C\).

b) Vì\(M,N\) lần lượt là trung điểm của \(AB\) và \(AC\)

\( \Rightarrow \,\,MN\) là đường trung bình của \(\Delta ABC\)và \(MN\) // \(BC\).

Mặt khác \(MN = ND\,\, \Rightarrow MN + ND = BC\)

\( \Rightarrow \,\,MD = BC\) (vì \(M,N,D\) thẳng hàng).

Mà \(MD\) // \(BC\) (do \(MN\) // \(BC\))

\( \Rightarrow \,\,BCDM\) là hình bình hành (vì có \(2\) cạnh đối nhau song song và bằng nhau).

Câu 5:

a) Ta có:

\(\begin{array}{l}\;\;\;\;\;2{x^2} + {y^2} + 9 = 6x + 2xy\\ \Leftrightarrow 2{x^2} + {y^2} + 9 – 6x – 2xy = 0\\ \Leftrightarrow \left( {{x^2} – 2xy + {y^2}} \right) + \left( {{x^2} – 6x + 9} \right) = 0\\ \Leftrightarrow {(x – y)^2} + {(x – 3)^2} = 0\end{array}\)

Vì \({(x – y)^2} \ge 0\,,\,\,{(x – 3)^2} \ge 0\,\,(\forall x,y)\) nên suy ra \({(x – y)^2} + {(x – 3)^2} \ge 0\).

Dấu \( = \) xảy ra khi \( \Leftrightarrow \left\{ \begin{array}{l}x – y = 0\\x – 3 = 0\end{array} \right. \Leftrightarrow x = y = 3\).

\(\begin{array}{l}A = {x^{2017}}{y^{2018}} – {x^{2018}}{y^{2017}} + \dfrac{1}{9}xy = {(xy)^{2017}}(y – x) + \dfrac{1}{9}xy\\ \Rightarrow A = {(3.3)^{2017}}(3 – 3) + \dfrac{1}{9}.3.3\\ \Rightarrow A = 1\end{array}\)

Vậy giá trị của biểu thức là \(A = {x^{2017}}{y^{2018}} – {x^{2018}}{y^{2017}} + \dfrac{1}{9}xy\) là \(1\) .

b) Vì \(\dfrac{{a + b}}{2} = 1 \Rightarrow a + b = 2 \Rightarrow b = 2 – a\).

Thay \(b = 2 – a\) vào biểu thức \(2{a^2} + 2{b^2} + 2008\) ta được:

\(\begin{array}{l}2{a^2} + 2{b^2} + 2008 = 2{a^2} + 2{(2 – a)^2} + 2008\\ = 2{a^2} + 2.(4 – 4a + {a^2}) + 2008\\ = 2{a^2} + 8 – 8a + 2{a^2} + 2008\\ = 4{a^2} – 8a + 2016\\ = 4{a^2} – 8a + 4 + 2012\\ = 4{(a – 1)^2} + 2012 \ge 2012\,\,(do\,\,{(a – 1)^2} \ge 0,\,\,\forall a)\\ \Rightarrow \dfrac{{2011}}{{2{a^2} + 2{b^2} + 2008}} \le \dfrac{{2011}}{{2012}}\,\,(\forall a)\end{array}\)

Vậy giá trị lớn nhất của biểu thức \(\dfrac{{2011}}{{2{a^2} + 2{b^2} + 2008}}\) là \(\dfrac{{2011}}{{2012}}\).

Dấu “\( = \)”  xảy ra khi \(a = b = 1\).