
I. HÀM SỐ
1. Định nghĩa
Cho \(D \subset \mathbb{R},\,\,D \ne \emptyset \). Hàm số \(f\) xác định trên $D$ là một qui tắc đặt tương ứng mỗi số \(x \in D\) với một và chỉ một số \(y \in \mathbb{R}\).
2. Tập xác định
Tập xác định của hàm số $y = f\left( x \right)$ là tập hợp tất cả các số thực $x$ sao cho biểu thức \(f\left( x \right)\) có nghĩa.
3. Sự biến thiên
Cho hàm số \(f\) xác định trên \(K\).
Hàm số $y = f\left( x \right)$ đồng biến (tăng) trên \(K\) nếu \(\forall {x_1},{x_2} \in K:{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\)
Hàm số $y = f\left( x \right)$ nghịch biến (giảm) trên \(K\) nếu \(\forall {x_1},{x_2} \in K:{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)
4. Tính chẵn lẻ
Cho hàm số $y = f\left( x \right)$ có tập xác định $D$.
Hàm số \(f\) được gọi là hàm số chẵn nếu với \(\forall x \in D\) thì \( – x \in D\) và $f\left( {-x} \right) = f\left( x \right)$ .
Hàm số \(f\) được gọi là hàm số lẻ nếu với \(\forall x \in D\) thì \( – x \in D\) và $f\left( {-x} \right) = – f\left( x \right)$ .
Chú ý: + Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
+ Đồ thị của hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
5. Tịnh tiến đồ thị hàm số
Định lý: Cho \(\left( G \right)\) là đồ thị của $y = f\left( x \right)$ và \(p > 0,\,\,q > 0\); ta có
Tịnh tiến \(\left( G \right)\) lên trên $q$ đơn vị thì được đồ thị $y = f\left( x \right) + q$
Tịnh tiến \(\left( G \right)\) xuống dưới $q$ đơn vị thì được đồ thị $y = f\left( x \right)-q$
Tịnh tiến \(\left( G \right)\) sang trái $p$ đơn vị thì được đồ thị $y = f\left( {x + p} \right)$
Tịnh tiến \(\left( G \right)\) sang phải $p$ đơn vị thì được đồ thị $y = f\left( {x-p} \right)$
II. HÀM SỐ BẬC NHẤT
1. Định nghĩa
Hàm số bậc nhất là hàm số có dạng \(y = ax + b\) \((a \ne 0)\).
2. Sự biến thiên
\( \bullet {\rm{ }}\)TXĐ: \(D = \mathbb{R}\)
\( \bullet {\rm{ }}\)Hàm số số đồng biến khi \(a > 0\) và nghịch biến khi \(a < 0\)
Bảng biến thiên:

3. Đồ thị
Đồ thị của hàm số \(y = ax + b\) \((a \ne 0)\) là một đường thẳng \(d\) có hệ số góc bằng \(a\), cắt trục hoành tại \(A\left( { – \dfrac{b}{a};0} \right)\) và trục tung tại \(B\left( {0;b} \right)\)
Hệ số góc của đường thẳng \(d\) là \(a = \tan \alpha \) với \(\alpha \) là góc tạo bởi \(d\) và \(Ox\)
Chú ý:
\( \bullet {\rm{ }}\)Nếu \(a = 0 \Rightarrow y = b\) là hàm số hằng, đồ thị là đường thẳng song song hoặc trùng với trục hoành.
\( \bullet {\rm{ }}\) Phương trình \(x = a\) cũng là một đường thẳng(nhưng không phải là một hàm số) vuông góc với trục tọa độ và cắt tại điểm có hoành độ bằng a.
\( \bullet {\rm{ }}\)Cho đường thẳng $d$ có hệ số góc \(k\), $d$ đi qua điểm \(M\left( {{x_0};{y_0}} \right)\), khi đó phương trình của đường thẳng \(d\) là: \(y – {y_0} = a\left( {x – {x_0}} \right)\).
4. Đồ thị cùa hàm số chứa dấu giá trị tuyệt đối
Vẽ đồ thị \(\left( C \right)\) của hàm số \(y = \left| {ax + b} \right|\) ta làm như sau
Cách 1: Vẽ \(\left( {{C_1}} \right)\) là đường thẳng \(y = ax + b\) với phần đồ thị sao cho hoành độ\(x\) thỏa mãn $x \ge – \dfrac{b}{a}$ , Vẽ \(\left( {{C_2}} \right)\) là đường thẳng \(y = – ax – b\) lấy phần đồ thị sao cho $x < – \dfrac{b}{a}$. Khi đó \(\left( C \right)\) là hợp của hai đồ thị \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\).
Cách 2: Vẽ đường thẳng \(y = ax + b\) và \(y = – ax – b\) rồi xóa đi phần đường thẳng nằm dưới trục hoành. Phần đường thẳng nằm trên trục hoành chính là \(\left( C \right)\).
Chú ý:
\( \bullet \) Biết trước đồ thị $\left( C \right):y = f\left( x \right)$ khi đó đồ thị $\left( {{C_1}} \right):y = f\left( {\left| x \right|} \right)$ là gồm phần :
– Giữ nguyên đồ thị $\left( C \right)$ ở bên phải trục tung;
– Lấy đối xứng đồ thị $\left( C \right)$ ở bên phải trục tung qua trục tung.
\( \bullet \) Biết trước đồ thị $\left( C \right):y = f\left( x \right)$ khi đó đồ thị $\left( {{C_2}} \right):y = \left| {f\left( x \right)} \right|$ là gồm phần:
– Giữ nguyên đồ thị $\left( C \right)$ ở phía trên trục hoành
– Lấy đối xứng phần đồ thị $\left( C \right)$ phía dưới trục hoành qua trục hoành.
III. HÀM SỐ BẬC HAI
1. Định nghĩa
Hàm số bậc hai là hàm số có dạng \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
2. Sự biến thiên
\( \bullet {\rm{ }}\)TXĐ: \(D = \mathbb{R}\)
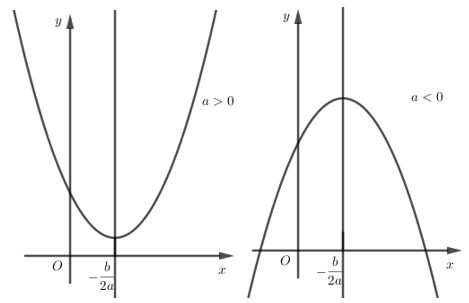
\( \bullet {\rm{ }}\)Khi \(a > 0\) hàm số đồng biến trên \(\left( { – \dfrac{b}{{2a}}; + \infty } \right)\), nghịch biến trên \(\left( { – \infty ; – \dfrac{b}{{2a}}} \right)\) và có giá trị nhỏ nhất là \( – \dfrac{\Delta }{{4a}}\) khi \(x = – \dfrac{b}{{2a}}\). Khi \(a < 0\) hàm số đồng biến trên \(\left( { – \infty ; – \dfrac{b}{{2a}}} \right)\), nghịch biến trên \(\left( { – \dfrac{b}{{2a}}; + \infty } \right)\) và có giá trị lớn nhất là \( – \dfrac{\Delta }{{4a}}\) khi \(x = – \dfrac{b}{{2a}}\)
Bảng biến thiên:

3. Đồ thị
Khi \(a > 0\) đồ thị hàm số bậc hai bề lõm hướng lên trên và có tọa độ đỉnh là \(I\left( { – \dfrac{b}{{2a}}; – \dfrac{\Delta }{{4a}}} \right)\)
Khi \(a < 0\) đồ thị hàm số bậc hai bề lõm hướng xuống dưới và có tọa độ đỉnh là \(I\left( { – \dfrac{b}{{2a}}; – \dfrac{\Delta }{{4a}}} \right)\)
Đồ thị nhận đường thẳng \(x = – \dfrac{b}{{2a}}\) làm trục đối xứng.
=======
Bài tập minh họa
Ví dụ 1:
Cho các hàm số : \(y = – 2x + 3,\,\,y = x + 2,\,\,y = \frac{3}{2}\).
a) Vẽ đồ thị các hàm số trên.
b) Dựa vào đồ thị hãy xác định giao điểm của các đồ thị hàm số đó.
Hướng dẫn:
a) Đồ thị hàm số \(y = – 2x + 3\) đi qua \(A\left( {0;3} \right),\,\,B\left( {\frac{3}{2};0} \right)\)
Đồ thị hàm số \(y = x + 2\) đi qua \(A’\left( {0;2} \right),\,\,B’\left( { – 2;0} \right)\)
Đồ thị hàm số \(y = \frac{3}{2}\) đi qua \(M\left( {0;\frac{3}{2}} \right)\) và song song với trục hoành.
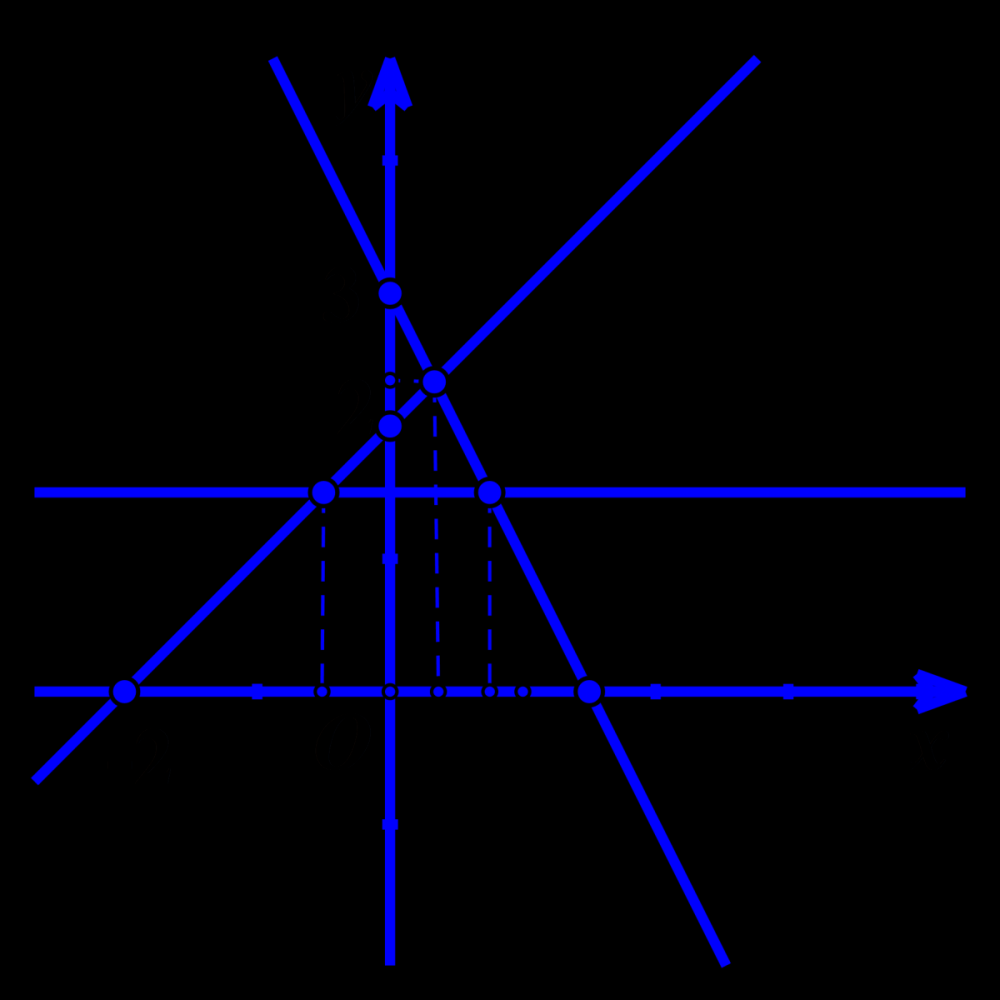
b) Giao điểm của hai đồ thị hàm số \(y = – 2x + 3,\,\,y = x + 2\) là \({M_1}\left( {\frac{1}{3};\frac{7}{3}} \right)\).
Giao điểm của hai đồ thị hàm số \(y = – 2x + 3,\,\,y = \frac{3}{2}\) là \({M_2}\left( {\frac{3}{4};\frac{3}{2}} \right)\).
Giao điểm của hai đồ thị hàm số \(\,y = x + 2,\,\,y = \frac{3}{2}\) là \({M_2}\left( { – \frac{1}{2};\frac{3}{2}} \right)\).
Ví dụ 2:
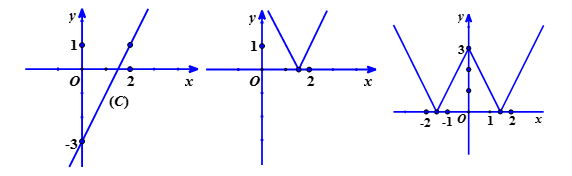
Vẽ đồ thị hàm số \(y = 2x – 3.\) Từ đó suy ra đồ thị của:
\(\left( {{C_1}} \right):y = 2\left| x \right| – 3,\) \(\left( {{C_2}} \right):y = \left| {2x – 3} \right|,\) \(\left( {{C_3}} \right):y = \left| {2\left| x \right| – 3} \right|\)
Hướng dẫn:
Đồ thị hàm số \(y = 2x – 3\) đi qua \(A\left( {0; – 3} \right),\,\,B\left( {2;1} \right)\) ta gọi là \(\left( C \right)\)
\(\bullet \) Khi đó đồ thị hàm số \(\left( {{C_1}} \right):y = 2\left| x \right| – 3\) là phần được xác định như sau
Ta giữ nguyên đồ thị \(\left( C \right)\) ở bên phải trục tung; lấy đối xứng đồ thị \(\left( C \right)\) ở phần bên phải trục tung qua trục tung.
\(\bullet \) \(\left( {{C_2}} \right):y = \left| {2x – 3} \right|\) là phần đồ thị \(\left( C \right)\) nằm phái trên trục hoành và đồ thị lấy đối xứng qua trục hoành của phần nằm trên trục hoành của \(\left( C \right)\).
\(\bullet \) \(\left( {{C_3}} \right):y = \left| {2\left| x \right| – 3} \right|\) là phần đồ thị \(\left( {{C_1}} \right)\) nằm phái trên trục hoành và đồ thị lấy đối xứng qua trục hoành của phần nằm trên trục hoành của \(\left( {{C_1}} \right)\).
Ví dụ 3:
Xác định phương trình của Parabol (P): \(y = {x^2} + bx + c\) trong các trường hợp sau:
a) (P) đi qua điểm \(A\left( {1;{\rm{ }}0} \right)\) và \(B\left( { – 2; – 6} \right)\).
b) (P) có đỉnh \(I\left( {1;{\rm{ }}4} \right)\).
c) (P) cắt trục tung tại điểm có tung độ bằng 3 và có đỉnh \(S\left( { – 2; – 1} \right)\).
Hướng dẫn:
a) Vì (P) đi qua A, B nên \(\left\{ \begin{array}{l}0 = 1 + b + c\\ – 6 = 4 – 2b + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b + c = – 1\\2b – c = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\c = – 4\end{array} \right.\).
Vậy (P):\(y = {x^2} + 3x–4\) .
b) Vì (P) có đỉnh \(I\left( {1;{\rm{ }}4} \right)\) nên\(\left\{ \begin{array}{l}\frac{{ – b}}{2} = 1\\ – \frac{{{b^2} – 4c}}{4} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = – 2\\c = 5\end{array} \right.\).
Vậy (P):\(y = {\rm{ }}{x^2}–2x + 5\) .
c) (P) cắt Oy tại điểm có tung độ bằng 3 suy ra \(c = 3\)
(P) có đỉnh \(S\left( { – 2; – 1} \right)\)suy ra: \(\left\{ \begin{array}{l} – \frac{b}{{2a}} = – 2\\ – 1 = 4a – 2b + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4\\a = 1\end{array} \right.\)
Ví dụ 4:
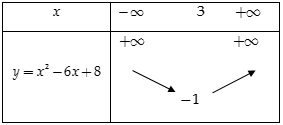
Cho hàm số \(y = {x^2} – 6x + 8\)
a) Lập bảng biến thiên và vẽ đồ thị các hàm số trên.
b) Sử dụng đồ thị để biện luận theo tham số \(m\) số điểm chung của đường thẳng \(y = m\) và đồ thị hàm số trên.
c) Sử dụng đồ thị, hãy nêu các khoảng trên đó hàm số chỉ nhận giá trị dương.
d) Sử dụng đồ thị, hãy tìm giá trị lớn nhất, nhỏ nhất của hàm số đã cho trên \(\left[ { – 1;5} \right]\).
Hướng dẫn:
a) Ta có \( – \frac{b}{{2a}} = 3,\,\, – \frac{\Delta }{{4a}} = – 1\)
Bảng biến thiên:
Suy ra đồ thị hàm số \(y = {x^2} + 3x + 2\) có đỉnh là \(I\left( {3; – 1} \right)\), đi qua các điểm \(A\left( {2;0} \right),\,\,B\left( {4;0} \right)\)
Nhận đường thẳng x = 3\) làm trục đối xứng và hướng bề lõm lên trên.
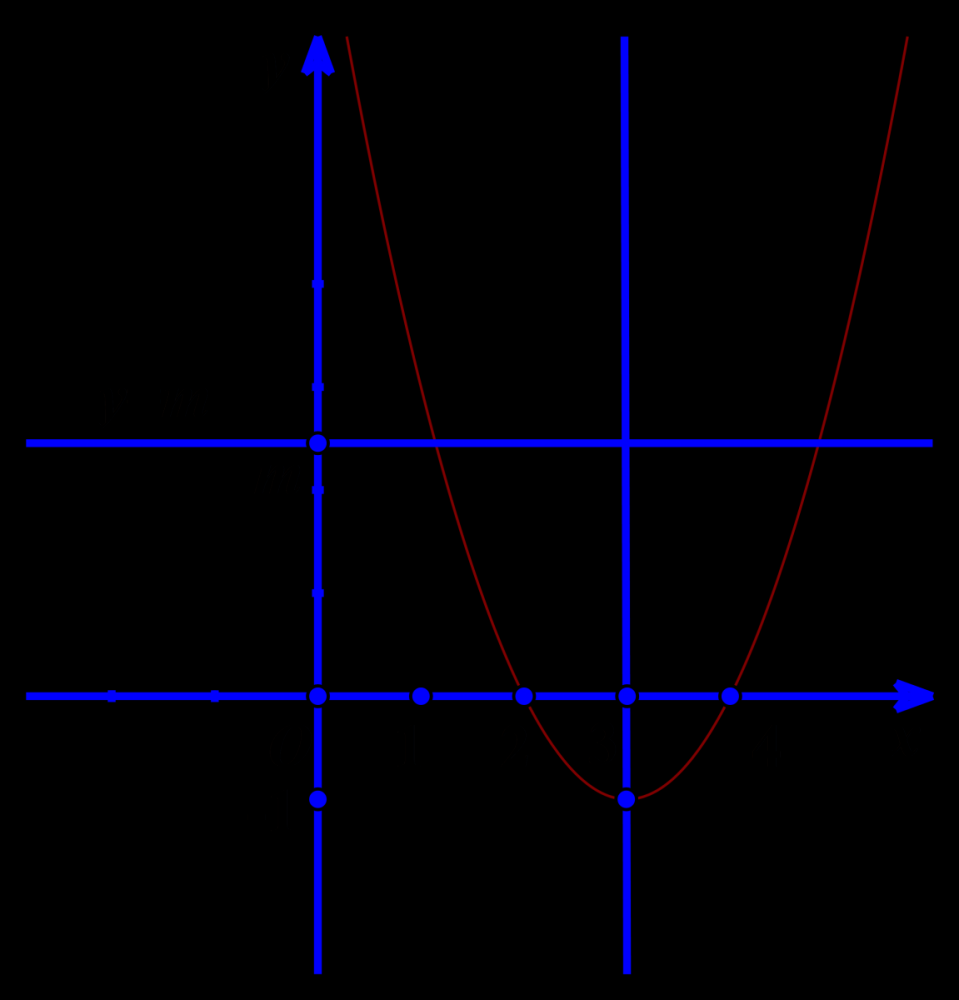
b) Đường thẳng \(y = m\) song song hoặc trùng với trục hoành do đó dựa vào đồ thị ta có
Với \(m < – 1\) đường thẳng \(y = m\) và parabol \(y = {x^2} – 6x + 8\) không cắt nhau
Với \(m = – 1\) đường thẳng \(y = m\) và parabol \(y = {x^2} – 6x + 8\) cắt nhau tại một điểm(tiếp xúc)
Với \(m > – 1\) đường thẳng \(y = m\) và parabol \(y = {x^2} – 6x + 8\) cắt nhau tại hai điểm phân biệt
c) Hàm số nhận giá trị dương ứng với phần đồ thị nằm hoàn toàn trên trục hoành
Do đó hàm số chỉ nhận giá trị dương khi và chỉ khi \(x \in \left( { – \infty ;2} \right) \cup \left( {4; + \infty } \right)\).
d) Ta có \(y\left( { – 1} \right) = 15,\,\,y\left( 5 \right) = 13,\,\,y\left( 3 \right) = – 1\), kết hợp với đồ thị hàm số suy ra
\(\mathop {\max }\limits_{\left[ { – 1;5} \right]} y = 15\) khi và chỉ khi\(x = – 1\)
\(\mathop {\min }\limits_{\left[ { – 1;5} \right]} y = – 1\) khi và chỉ khi \(x = 3\)
