Ôn tập Chương 2 – Tích vô hướng của hai vectơ và ứng dụng

Bài 1:
Tìm giá trị của mỗi biểu thức sau:
\(A = 2\sin {30^0} – 3\cos {45^0} + 4\cos {60^0}\)\( – 5\sin {120^0} + 6\cos {150^0}.\)
\(B = 3{\sin ^2}{45^0} – 2{\cos ^2}{45^0} – 4{\sin ^2}{50^0}\)\( – 4{\cos ^2}{50^0} + 5\tan {55^0}{\mathop{\rm c}\nolimits} {\rm{ot5}}{{\rm{5}}^0}.\)
Giải
\(\begin{array}{l}A = 1 – \dfrac{{3\sqrt 2 }}{2} + 2 – \dfrac{{5\sqrt 3 }}{2} – \dfrac{{6\sqrt 3 }}{2}\\ = 3 – \dfrac{{11\sqrt 3 + 3\sqrt 2 }}{2}.\\B = \dfrac{3}{2} – 1 – 4 + 5 = \dfrac{3}{2}.\end{array}\)

Bài 2.  (6 điểm) Tam giác ABC có cạnh \(BC = 2\sqrt 3 \), cạnh AC = 2 và \(\widehat C = {30^0}\).

a) Tính cạnh AB và sinA;

b) Tính diện tích S của tam giác ABC;

c) Tính chiều cao \({h_a}\) và trung tuyến \({m_a}\)

Gợi ý làm bài

a)

\(\eqalign{
& {c^2} = {a^2} + {b^2} – 2ab\cos C \cr
& = 12 + 4 – 8\sqrt 3 .cos{30^0} \cr} \)

\({c^2} = 4 =  > c = 2\) hay AB = 2.

\(\sin A = {{a\sin C} \over c} = {{2\sqrt 3 .{1 \over 2}} \over 2} = {{\sqrt 3 } \over 2}\)

b) \(S = {1 \over 2}ab\sin C = {1 \over 2}.2\sqrt 3 .2.{1 \over 2} = \sqrt 3 \)

c) \({h_a} = {{2S} \over a} = {{2\sqrt 3 } \over {2\sqrt 3 }} = 1,{m_a} = 1\)

Bài 3.  (4 điểm) Cho tam giác ABC có cạnh BC, AC và AB có độ dài lần lượt là a = 3, b = 4, c = 6.

a) Tính cô sin của góc lớn nhất của tam giác ABC;

b) Tính đường cao ứng với cạnh lớn nhất.

Đáp án

a)Cạnh c lớn nhất suy ra góc C lớn nhất

\(\cos C = {{{a^2} + {b^2} – {c^2}} \over {2ab}} = {{9 + 16 – 36} \over {24}} = {{ – 11} \over {24}}\)

b) \({h_a} = {{2S} \over c} = {{ab\sin C} \over c} = {{3.4.\sqrt {455} } \over {6.24}} = {{\sqrt {455} } \over {12}}\)

---

Bài 4.

Cho tam giác ABC có BC = a, CA = b, AB = c.

a) Chứng minh rằng: \(\overrightarrow {AB} .\overrightarrow {AC}  = {{{b^2} + {c^2} – {a^2}} \over 2}\)

b) Chứng minh rằng: \(\overrightarrow {AB} .\overrightarrow {AC}  = A{I^2} – {{B{C^2}} \over 4}\) với I là trung điểm của BC;

c) Gọi G là trọng tâm của tam giác ABC, với M là điểm bất kì trong mặt phẳng, chứng minh hệ thức sau:

\(M{A^2} + M{B^2} + M{C^2} = G{A^2} + G{B^2} + G{C^2} + 3M{G^2}\)

Giải

a) Ta có: \(\overrightarrow {BC}  = \overrightarrow {AC}  – \overrightarrow {AB} \)

\(\eqalign{
& = > B{C^2} = {\overrightarrow {BC} ^2} = {(\overrightarrow {AC} – \overrightarrow {AB} )^2} \cr
& = A{C^2} + A{B^2} – 2\overrightarrow {AC} .\overrightarrow {AB} \cr} \)

\( \Leftrightarrow \overrightarrow {AC} .\overrightarrow {AB}  = {{A{C^2} + A{B^2} – B{C^2}} \over 2}\)

\(=  > \overrightarrow {AC} .\overrightarrow {AB}  = {{{b^2} + {c^2} – {a^2}} \over 2}\)

b) Ta có: \(\overrightarrow {AB}  = \overrightarrow {AI}  + \overrightarrow {IB} \) và \(\overrightarrow {AC}  = \overrightarrow {AI}  + \overrightarrow {IC}  = \overrightarrow {AI}  – \overrightarrow {IB} \)

\( =  > \overrightarrow {AC} .\overrightarrow {AB}  = A{I^2} – I{B^2} = A{I^2} – {{B{C^2}} \over 4}\) (I là trung điểm của BC)

c) Ta có:

\(M{A^2} + M{B^2} + M{C^2} = G{A^2} + G{B^2} + G{C^2} + 3M{G^2}\)

\( \Leftrightarrow (M{A^2} – G{A^2}) + (M{B^2} – G{B^2}) + (M{C^2} – G{C^2}) = 3M{G^2}\)

\( \Leftrightarrow (\overrightarrow {MA}  – \overrightarrow {GA)} (\overrightarrow {MA}  + \overrightarrow {GA} ) + (\overrightarrow {MB}  – \overrightarrow {GB} )(\overrightarrow {MB}  + \overrightarrow {GB} ) + (\overrightarrow {MC}  – \overrightarrow {GC} )(\overrightarrow {MC}  + \overrightarrow {GC} ) = 3M{G^2}\)

\( \Leftrightarrow \overrightarrow {MG} (\overrightarrow {MA}  + \overrightarrow {GA}  + \overrightarrow {MB}  + \overrightarrow {GB}  + \overrightarrow {MC}  + \overrightarrow {GC} ) = 3M{G^2}\)

\(\Leftrightarrow \overrightarrow {MG} {\rm{[}}(\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC} ) + (\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC} ){\rm{]}} = 3M{G^2}\)

\( \Leftrightarrow \overrightarrow {MG} (3\overrightarrow {MG}  + \overrightarrow 0 ) = 3M{G^2}\)

\(\Leftrightarrow 3{\overrightarrow {MG} ^2} = 3M{G^2}\) (đúng)

Vậy đẳng thức được chứng minh.

---

Bài 5.
Cho tam giác \(ABC\) có \(\widehat A = {60^0} , a = 10 , r = \dfrac{{5\sqrt 3 }}{3}\).
a) Tính \(R.\)
b) Tính \(b, c.\)
Giải

a) Ta có
\(2R = \dfrac{a}{{\sin A}} = \dfrac{{10}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{20\sqrt 3 }}{3} \)
\( \Rightarrow R = \dfrac{{10\sqrt 3 }}{3}\).
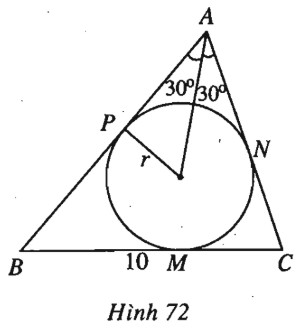
b) Gọi \(M, N, P\) lần lượt là các tiếp điểm của \(BC, CA, AB\) với đường tròn nội tiếp tam giác \(ABC\) (h.72).
Ta có \(AP = AN = r.\cot {30^0} = 5 ; \)
\(BP + NC = BM + MC = a = 10\).
Từ đó ta có \((b – AN) + (c – AP) = 10\) hay \(b+c=20.\) (1)
Theo định lí cosin
\({a^2} = {b^2} + {c^2} – 2bc\cos {60^0}\) hay \({a^2} = {(b + c)^2} – 2bc – bc\), suy ra
\(bc = \dfrac{{{{(b + c)}^2} – {a^2}}}{3}\) \( = \dfrac{{{{20}^2} – {{10}^2}}}{3} = 100\) (2)
Từ (1) và (2) suy ra \(b, c\) là nghiệm của phương trình bậc hai \({x^2} – 20x + 100 = 0\).
Phương trình này có nghiệm kép \(b=c=10\) nên \(ABC\) là tam giác đều.