Giải SBT Bài 3. Đường thẳng và mặt phẳng song song chương 2 hình học 11

Bài 2.16 trang 74 SBT Hình 11

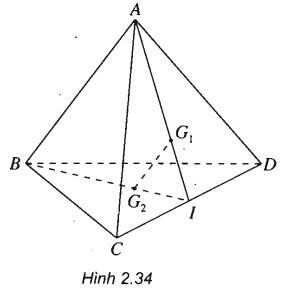
Cho tứ diện ABCD. Gọi G₁ và G₂  lần lượt là trọng tâm của tam giác ACD và BCD. Chứng minh rằng G₁G₂ song song với các mặt phẳng (ABC) và (ABD).

Gọi I là trung điểm của CD.

Vì G₁ là trọng tâm của tam giác ACD nên \({G_1} \in AI\)

Vì G₂ là trọng tâm của tam giác BCD nên \({G_2} \in BI\)

Ta có :

\(\left\{ \matrix{
{{I{G_1}} \over {IA}} = {1 \over 3} \hfill \cr
{{I{G_2}} \over {IB}} = {1 \over 3} \hfill \cr} \right. \Rightarrow {{I{G_1}} \over {IA}} = {{I{G_2}} \over {IB}} \Rightarrow {G_1}{G_2}\parallel AB\)

\(AB \subset \left( {ABC} \right) \Rightarrow {G_1}{G_2}\parallel \left( {ABC} \right)\)

Và \(AB \subset \left( {ABD} \right) \Rightarrow {G_1}{G_2}\parallel \left( {ABD} \right)\)

Bài 2.17 trang 74 Sách bài tập Toán 11

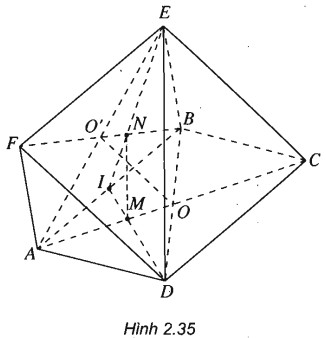
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt .Gọi O là giao điểm của AC và BD, O’ là giao điểm của AE và BF.

a) Chứng minh rằng OO’ song song với hai mặt phẳng (ADF) và (BCE)

b) Gọi M và N lần lượt là trọng tâm của các tam giác ABDvà ABE. Chứng minh rằng .

a) Ta có : \(OO’\parallel DF\) ( đường trung bình của tam giác BDF).

Vì \(DF \subset \left( {ADF} \right) \Rightarrow OO’\parallel \left( {ADF} \right)\).

Tương tự \(OO’\parallel EC\) (đường trung bình của tam giác AEC).

Vì \(EC \subset \left( {BCE} \right)\) nên \(OO’\parallel \left( {BCE} \right)\).

b) Gọi I là trung điểm AB;

Vì M là trọng tâm của tam giác ABD nên \(M \in DI\)

Vì N là trọng tâm của tam giác ABE nên \(N \in EI\)

Ta có :

\(\left\{ \matrix{
{{IM} \over {I{\rm{D}}}} = {1 \over 3} \hfill \cr
{{IN} \over {IE}} = {1 \over 3} \hfill \cr} \right. \Rightarrow {{IM} \over {I{\rm{D}}}} = {{IN} \over {IE}} \Rightarrow MN\parallel DE\)

Mà

\(\left\{ \matrix{
C{\rm{D}}\parallel AB \hfill \cr
C{\rm{D}} = AB \hfill \cr
EF\parallel AB \hfill \cr
EF = AB \hfill \cr} \right.\)

Nên \(C{\rm{D}}\parallel EF\) và \(C{\rm{D  =  }}EF\), suy ra tứ giác CDFE là hình bình hành.

\(\left\{ \matrix{
MN\parallel DE \hfill \cr
DE \subset \left( {CEF} \right) \hfill \cr} \right. \Rightarrow MN\parallel \left( {CEF} \right)\)

Bài 2.18 trang 74

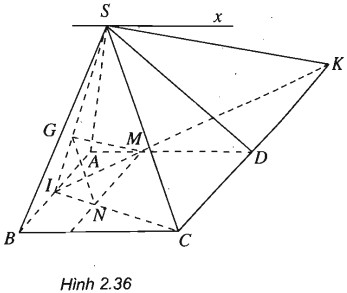
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD = 3AM

a)  Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).

b) Đường thẳng qua M song song với AB cắt CI tại N. Chứng minh rằng \(NG\parallel \left( {SC{\rm{D}}} \right)\).

c) Chứng minh rằng \(MG\parallel \left( {SC{\rm{D}}} \right)\).

a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).

Ta có:

\(\left\{ \matrix{
A{\rm{D}} \subset \left( {SA{\rm{D}}} \right) \hfill \cr
BC \subset \left( {SBC} \right) \hfill \cr
A{\rm{D}}\parallel BC \hfill \cr} \right.\)

\( \Rightarrow \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right) = Sx\)

Và \(Sx\parallel AD\parallel BC\).

b) Ta có: \(MN\parallel IA\parallel C{\rm{D}}\)

\( \Rightarrow {{AM} \over {A{\rm{D}}}} = {{IN} \over {IC}} = {1 \over 3}\)

Mà \({{IG} \over {IS}} = {1 \over 3}\) ( G là trọng tâm của ∆SAB) nên \({{IG} \over {IS}} = {{IN} \over {IC}} = {1 \over 3} \Rightarrow GN\parallel SC\)

\(SC \subset \left( {SC{\rm{D}}} \right) \Rightarrow GN\parallel \left( {SC{\rm{D}}} \right)\)

c) Giả sử IM cắt CD tại \(K \Rightarrow SK \subset \left( {SC{\rm{D}}} \right)\)

\(MN\parallel C{\rm{D}} \Rightarrow {{MN} \over {CK}} = {{IN} \over {IC}} = {1 \over 3} \Rightarrow {{IM} \over {IK}} = {1 \over 3}\)

Ta có:

\(\left\{ \matrix{
{{IG} \over {IS}} = {1 \over 3} \hfill \cr
{{IM} \over {IK}} = {1 \over 3} \hfill \cr} \right. \Rightarrow GM\parallel SK \Rightarrow GM\parallel \left( {SC{\rm{D}}} \right)\)

Bài 2.19 trang 74 SBT Hình học 11

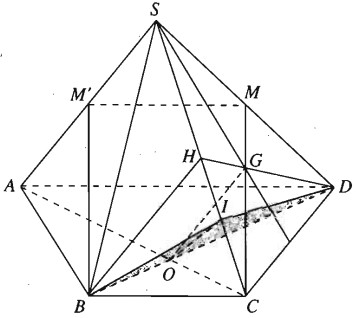
Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn là AD và AD = 2BC. Gọi O là giao điểm của AC và BD, G là trọng tâm của tam giác SCD.

a) Chứng minh rằng \(OG\parallel \left( {SBC} \right)\)

b) Cho M là trung điểm của SD. Chứng minh rằng \(CM\parallel \left( {SAB} \right)\).

c) Giả sử điểm I nằm trong đoạn SC sao cho \(S{\rm{C = }}{3 \over 2}SI\). Chứng minh rằng \(SA\parallel \left( {BI{\rm{D}}} \right)\).

Giải:

a) Gọi H là trung điểm của SC

Ta có:

\({{DG} \over {DH}} = {2 \over 3} \,\,\,\,\, \left( 1 \right)\)

\(BC\parallel A{\rm{D}} \Rightarrow {{O{\rm{D}}} \over {OB}} = {{OA} \over {OC}} = {{AD} \over {BC}} = 2\)

\( \Rightarrow O{\rm{D}} = 2{\rm{O}}B\)

\( \Rightarrow {{O{\rm{D}}} \over {B{\rm{D}}}} = {2 \over 3} \,\,\,\, \left( 2 \right)\)

Từ (1) và (2) \(\Rightarrow {{DG} \over {DH}} = {{O{\rm{D}}} \over {B{\rm{D}}}} \Rightarrow OG\parallel BH\)

\(BH \subset \left( {SBC} \right) \Rightarrow OG\parallel \left( {SBC} \right)\)

b) Gọi M’ là trung điểm của \(SA \Rightarrow MM’\parallel A{\rm{D}}\) và \(MM’ = {{A{\rm{D}}} \over 2}\). Mặt khác vì \(BC\parallel A{\rm{D}}\) và \(BC = {{A{\rm{D}}} \over 2}\) nên \(BC\parallel MM’\) và \(BC = MM’\).

Do đó tứ giác BCMM’ là hình bình hành \( \Rightarrow CM\parallel BM’\) mà \(BM’ \subset \left( {SAB} \right)\)

\( \Rightarrow CM\parallel \left( {SAB} \right)\)

c) Ta có: \({{OC} \over {OA}} = {1 \over 2}\) nên \({{OC} \over {CA}} = {1 \over 3}\). Mặt khác vì \(SC = {3 \over 2}SI\) nên \({{CI} \over {CS}} = {1 \over 3}\).

\({{OC} \over {CA}} = {{CI} \over {CS}} \Rightarrow OI\parallel SA\)

\(OI \subset \left( {BID} \right) \Rightarrow SA\parallel \left( {BID} \right)\)

Bài 2.20 trang 74 Sách bài tập (SBT) Hình học 11

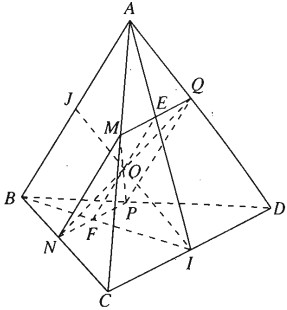
Cho tứ diện ABCD. Qua điểm M nằm trên AC ta dựng một mặt phẳng \(\left( \alpha  \right)\) song song với AB và CD. Mặt phẳng này lần lượt cắt các cạnh BC, BD và AD tại N, P và Q.

a) Tứ giác MNPQ là hình gì?

b) Gọi O là giao điểm hai đường chéo của tứ giác MNPQ. Tìm tập hợp các điểm O khi M di động trên đoạn AC.

Giải:

a)

\(\left\{ \matrix{
\left( \alpha \right)\parallel AB \hfill \cr
AB \subset \left( {ABC} \right) \hfill \cr} \right.\)

\( \Rightarrow \left( \alpha  \right) \cap \left( {ABC} \right) = MN\) và \(MN\parallel AB\)

Ta có \(N \in \left( {BC{\rm{D}}} \right)\)

Và  \(\left\{ \matrix{\left( \alpha \right)\parallel C{\rm{D}} \hfill \cr C{\rm{D}} \subset \left( {BCD} \right) \hfill \cr} \right.\)

Nên \( \Rightarrow \left( \alpha  \right) \cap \left( {BCD} \right) = NP\) và \(NP\parallel C{\rm{D}}\)

Ta có \(P \in \left( {AB{\rm{D}}} \right)\)

Và  \(\left\{ \matrix{\left( \alpha \right)\parallel AB \hfill \cr AB \subset \left( {ABD} \right) \hfill \cr} \right.\) nên \( \Rightarrow \left( \alpha  \right) \cap \left( {ABD} \right) = PQ\) và \(PQ\parallel AB\)

\(\left\{ \matrix{
Q \in \left( {ACD} \right) \hfill \cr
\left( \alpha \right)\parallel C{\rm{D}} \hfill \cr} \right.\) nên \( \Rightarrow \left( \alpha  \right) \cap \left( {ACD} \right) = MQ\) và \(MQ\parallel C{\rm{D}}\)

Do đó \(MN\parallel PQ\) và \(NP\parallel MQ\), Vậy tứ giác MNPQ là hình bình hành.

b)  Ta có: \(MP \cap NQ = O\). Gọi I là trung điểm của CD.

Trong tam giác ACD có : \(MQ\parallel C{\rm{D}} \Rightarrow AI\) cắt MQ tại trung điểm E của MQ.

Trong tam giác ACD có : \(NP\parallel C{\rm{D}} \Rightarrow BI\) cắt NP tại trung điểm F của NP.

Vì MNPQ là hình bình hành nên ta có

\(\left\{ \matrix{
EF\parallel MN \hfill \cr
O\,là\,trung\,điểm\,EF\, \hfill \cr} \right.\)

\(EF\parallel MN \Rightarrow EF\parallel AB\)

Trong ∆ABI ta có \(EF\parallel AB\) suy ra : IO cắt AB tại trung điểm J

\( \Rightarrow I,O,J\) thẳng hàng

\( \Rightarrow O \in IJ\) cố định.

Vì M di động trên đoạn AC nên Ochạy trong đoạn IJ . Vậy tập hợp các điểm O là đoạn IJ.

Bài 2.21 trang 75 SBT Toán hình 11

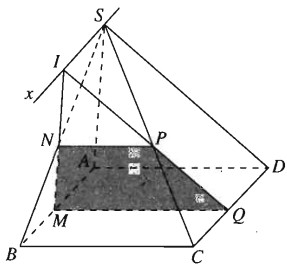
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. M là một điểm di động trên đoạn AB. Một mặt phẳng \(\left( \alpha  \right)\) đi qua M và song song với SA và BC; \(\left( \alpha  \right)\) cắt SB, SC và CD lần lượt tại N, P và Q

a) Tứ giác MNPQ là hình gì?

b) Gọi I là giao điểm của MN và PQ. Chứng minh rằng I nằm trên một đường thẳng cố định.

a) Vì \(M \in \left( {SAB} \right)\)

Và \(\left\{ \matrix{\left( \alpha \right)\parallel SA \hfill \cr SA \subset \left( {SAB} \right) \hfill \cr} \right.\) nên \(\left( \alpha  \right) \cap \left( {SAB} \right) = MN\)

và \(MN\parallel SA\)

Vì \(N \in \left( {SBC} \right)\)

Và \(\left\{ \matrix{\left( \alpha \right)\parallel BC \hfill \cr BC \subset \left( {SBC} \right) \hfill \cr} \right.\) nên \(\left( \alpha  \right) \cap \left( {SBC} \right) = NP\)

và \(NP\parallel BC \,\,\, \left( 1 \right)\)

\(\left\{ \matrix{
P,Q \in \left( \alpha \right) \hfill \cr
P,Q \in \left( {SC{\rm{D}}} \right) \hfill \cr} \right. \Rightarrow \left( \alpha \right) \cap \left( {SC{\rm{D}}} \right) = PQ\)

\(Q \in C{\rm{D}} \Rightarrow Q \in \left( {ABC{\rm{D}}} \right)\)

Và\(\left\{ \matrix{\left( \alpha \right)\parallel BC \hfill \cr BC \subset \left( {ABCD} \right) \hfill \cr} \right.\) nên \(\left( \alpha  \right) \cap \left( {ABCD} \right) = QM\)

và \(QM\parallel BC \,\,\, \left( 2 \right)\)

Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.

b) Ta có:

\(\left\{ \matrix{
S \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right) \hfill \cr
AB \subset \left( {SAB} \right),C{\rm{D}} \subset \left( {SC{\rm{D}}} \right) \hfill \cr
AB\parallel C{\rm{D}} \hfill \cr} \right. \Rightarrow \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right) = Sx\) và \(S{\rm{x}}\parallel AB\parallel C{\rm{D}}\)

\(MN \cap PQ = I \Rightarrow \left\{ \matrix{
I \in MN \hfill \cr
I \in PQ \hfill \cr} \right.\)

\(MN \subset \left( {SAB} \right) \Rightarrow I \in \left( {SAB} \right),PQ \subset \left( {SC{\rm{D}}} \right) \Rightarrow I \in \left( {SC{\rm{D}}} \right)\)

\( \Rightarrow I \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right) \Rightarrow I \in Sx\)

(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.