GIẢI CHI TIẾT Giải SBT Bài 27 Chương 9 – SBT Toán 10 KNTT
============
Giải bài 9.7 trang 66 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Tại một quán ăn, lúc đầu có 50 khách trong đó có 2x đàn ông và y phụ nữ. Sau một tiếng, y – 6 đàn ông ra về và 2x – 5 khách mới đến là nữ. Chọn ngẫu nhiên một khách. Biết rằng xác suất để chọn được một khách nữ là \(\frac{9}{{13}}\). Tìm x và y.
Phương pháp giải
Sử dụng công thức xác suất cổ điển \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Lời giải chi tiết
Ta có \(2x + y = 50 \Rightarrow y = 50 – 2x\). Sau một tiếng, trong quán có \(50 – \left( {y – 6} \right) + 2x – 5 = 51 + 2x – y\) người, trong đó có \(2x – 5 + y\) là nữ. Vậy ta có
\(\begin{array}{l}\frac{{2x – 5 + y}}{{51 + 2x – y}} = \frac{9}{{13}} \Leftrightarrow 8x + 22y = 524 \Leftrightarrow 4x + 11y = 262\\ \Leftrightarrow 4x + 11\left( {50 – 2x} \right) = 262 \Leftrightarrow 18x = 288 \Leftrightarrow x = 16\end{array}\)
Vậy \(x = 16 \Rightarrow y = 18\).
GIẢI SBT Toán 10 Kết nối tri thức Chương 9 Bài 27
Giải bài 9.8 trang 66 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Một lớp có 40 học sinh trong đó có 16 nam. Trong các em nam có 3 em thuận tay trái. Trong các em nữ có 2 em thuận tay trái. Chọn ngẫu nhiên hai em. Tính xác suất để hai em chọn được có một em nữ không thuận tay trái và một em nam thuận tay trái.
Phương pháp giải
Sử dụng công thức xác suất cổ điển \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Lời giải chi tiết
Ta có \(n\left( \Omega \right) = C_{40}^2 = 780\).
Gọi A là biến cố đang xét. Lớp có \(40 – 16 = 24\) nữ trong đó có \(24 – 2 = 22\) em không thuận tay trái.
Trong lớp có 3 em nam thuận tay trái. Do đó \(n\left( A \right) = 22.3 = 66\).
Vậy \(P\left( A \right) = \frac{{66}}{{780}} = \frac{{11}}{{130}}\).
GIẢI SBT Toán 10 Kết nối tri thức Chương 9 Bài 27
Giải bài 9.9 trang 66 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Có ba chiếc hộp trong đó hộp I có một viên bi đỏ, một viên bi xanh, một viên
bi vàng; hộp II có một viên bi xanh, một viên bi vàng; hộp III có một viên bi đỏ và một viên bi xanh. Tất cả các viên bi đều có cùng kích thước. Từ mỗi hộp rút ngẫu nhiên một viên bi.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất để trong ba viên bi rút ra có ít nhất một viên bi đỏ bằng cách tính gián tiếp thông qua tính xác suất của biến cố đối.
Phương pháp giải
Sử dụng công thức \(P\left( A \right) = 1 – P\left( {\overline A } \right) = 1 – \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}}\).
Lời giải chi tiết
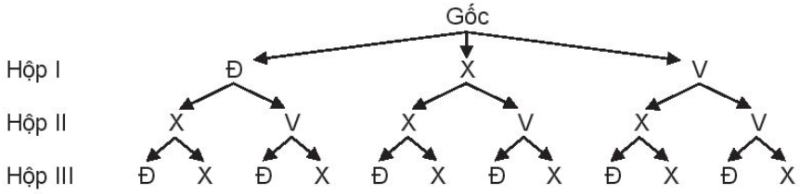
a) Kí hiệu Đ, X, V tương ứng là viên bi màu đỏ, xanh, vàng.

Dựa vào sơ đồ cây ta thấy \(n\left( \Omega \right) = 12\).
b) Gọi A là biến cố đang xét. Biến cố đối của \(A\) là \(\overline A \): “Trong ba viên bi không có viên bi màu đỏ”.
\(\overline A = \left\{ {XXX,XVX,VXX,VVX} \right\}\). Suy ra \(n\left( {\overline A } \right) = 4\). Vậy \(P\left( {\overline A } \right) = \frac{4}{{12}} = \frac{1}{3}\).
Do đó \(P\left( A \right) = 1 – P\left( {\overline A } \right) = 1 – \frac{1}{3} = \frac{2}{3}\).
GIẢI SBT Toán 10 Kết nối tri thức Chương 9 Bài 27
Giải bài 9.10 trang 66 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Có ba hộp đựng thẻ. Hộp I chứa các tấm thẻ đánh số {1; 2; 3}. Hộp II chứa các tấm thẻ đánh số {2; 4; 6; 8}. Hộp III chứa các tấm thẻ đánh số {1; 3; 5; 7; 9; 11}. Từ mỗi hộp rút ngẫu nhiên một tấm thẻ rồi cộng ba số trên ba tấm thẻ với nhau. Tính xác suất để kết quả là một số lẻ.
Phương pháp giải
Sử dụng công thức xác suất cổ điển \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Lời giải chi tiết
Ta có \(\Omega = \left\{ {\left( {a,b,c} \right)} \right\}\), trong đó \(a \in \left\{ {1;2;3} \right\},b \in \left\{ {2;4;6;8} \right\},c \in \left\{ {1;3;5;7;9;11} \right\}\). Suy ra \(n\left( \Omega \right) = 3.4.6 = 72\).
Gọi A là biến cố đang xét. Ta có \(A = \left\{ {\left( {a,b,c} \right),a + b + c = 2k + 1\left( {k \in \mathbb{Z}} \right)} \right\}\).
Vậy \(A = \left\{ {\left( {2,b,c} \right)} \right\}\) trong đó \(b \in \left\{ {2;4;6;8} \right\},c \in \left\{ {1;3;5;7;9;11} \right\}\). Suy ra \(n\left( A \right) = 1.4.6 = 24\).
Vậy \(P\left( A \right) = \frac{{24}}{{72}} = \frac{1}{3}\).
GIẢI SBT Toán 10 Kết nối tri thức Chương 9 Bài 27
Giải bài 9.11 trang 66 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Trên một dãy phố có 3 quán ăn A, B, C. Hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán để ăn trưa.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của các biến cố sau:
E: “Hai người cùng vào một quán”.
F: “Cả hai không chọn quán C.
Phương pháp giải
Sử dụng công thức xác suất cổ điển \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Lời giải chi tiết
a) Sơ đồ hình cây:

b) \(\Omega = \left\{ {{\rm{AA}},AB,AC,BA,BB,BC,CA,CB,CC} \right\}\).
Ta có \(E = \left\{ {{\rm{AA}},BB,CC} \right\}\). Vậy \(P\left( E \right) = \frac{3}{9} = \frac{1}{3}\).
\(F = \left\{ {{\rm{AA}},AB,BA,BB} \right\}\). Vậy \(P\left( F \right) = \frac{4}{9}\).
GIẢI SBT Toán 10 Kết nối tri thức Chương 9 Bài 27
Giải bài 9.12 trang 66 SBT Toán 10 Kết nối tri thức tập 2 – KNTT
Trên một phố có hai quán ăn A, B. Bốn bạn Sơn, Hải, Văn, Đạo mỗi người chọn ngẫu nhiên một quán ăn.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất để:
• Tất cả đều vào một quán;
• Mỗi quán có đúng 2 bạn vào;
• Quán A có 3 bạn vào, quán B có 1 bạn vào
• Một quán có 3 bạn vào, quán kia có 1 bạn vào.
Phương pháp giải
Sử dụng công thức xác suất cổ điển \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Lời giải chi tiết
a) Sơ đồ cây
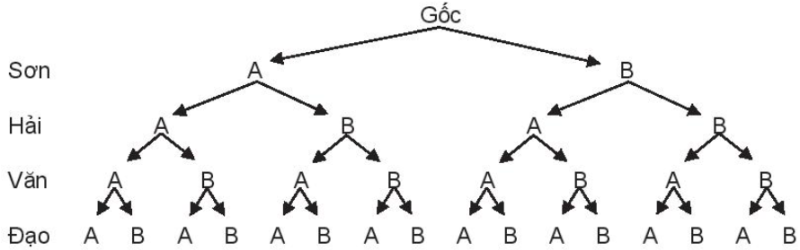
b) Ta có \(\Omega = \left\{ \begin{array}{l}AAAA;AAAB;AABA;AABB;ABAA;ABAB;ABBA;ABBB;\\BAAA;BAAB;BABA;BABB;BBAA;BBAB;BBBA;BBBB\end{array} \right\}\) .
Suy ra \(n\left( \Omega \right) = 16\).
+ Gọi \(E\) là biến cố \(E\): “Tất cả đều vào một quán”. \(E = \left\{ {AAAA,BBBB} \right\}\). Suy ra \(n\left( E \right) = 2 \Rightarrow P\left( E \right) = \frac{2}{{16}} = \frac{1}{8}\).
+ Gọi \(F\) là biến cố \(F\): “Mỗi quán có đúng hai bạn vào”. \(F = \left\{ {AABB,ABAB,ABBA,BAAB,BABA,BBAA} \right\}\). Suy ra \(n\left( F \right) = 6 \Rightarrow P\left( F \right) = \frac{6}{{16}} = \frac{3}{8}\).
+ Gọi \(G\) là biến cố \(G\): “Quán A có ba bạn vào, quán B có một bạn vào”.
\(G = \left\{ {AAAB;AABA;ABAA;BAAA} \right\}\). Suy ra \(n\left( G \right) = 4 \Rightarrow P\left( G \right) = \frac{4}{{16}} = \frac{1}{4}\).
+ Gọi K là biến cố K: “Một quán có ba bạn vào, quán kia có một bạn vào”.
Khi đó \(P\left( K \right) = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\).
GIẢI SBT Toán 10 Kết nối tri thức Chương 9 Bài 27
=========
THUỘC: Giải sách bài tập toán 10 – Kết nối
