Giải Sách bài tập Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng – CTST

Giải Sách bài tập Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng – SÁCH GIÁO KHOA CHÂN TRỜI SÁNG TẠO 2024

================

Giải SBT Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng

Giải SBT Toán 11 trang 55

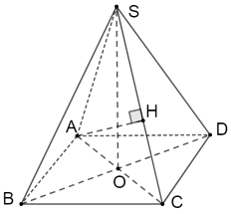
Bài 1 trang 55 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh $a\sqrt{2}$ . Biết rằng SA = SB = SC = SD, SO = $2a\sqrt{2}$ .

a) Chứng minh rằng SO ⊥ (ABCD).

b) Tính độ dài đường cao xuất phát từ đỉnh A của tam giác SAC.

Lời giải:

a)Từ giả thiết, dễ dàng nhận thấy ∆SAC và ∆SBD là các tam giác cân.

Ta có: 

Do đó SO ⊥ (ABCD)

b)Ta có: AC = 2a, OC = a, $SC=\sqrt{S{O}^2+O{C}^2}=3a.$

Vẽ đường cao AH của ∆SAC.

Ta có: $AH=\frac{SO.AC}{SC}=\frac{2a\sqrt{2}.2a}{3a}=\frac{4a\sqrt{2}}{3}.$

Vậy độ dài đường cao xuất phát từ đỉnh A của tam giác SAC bằng $\frac{4a\sqrt{2}}{3}$.

Bài 2 trang 55 SBT Toán 11 Tập 2: Cho tứ diện ABCD có AB ⊥ CD và AC ⊥ BD. Gọi H là hình chiếu vuông góc của A xuống mặt phẳng (BCD). Chứng minh rằng H là trực tâm của ∆BCD và AD ⊥ BC.

Lời giải:

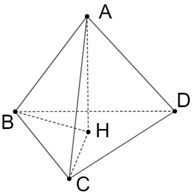
Theo giả thiết: 

Suy ra CD ⊥AHB

Do đó CD ⊥ BH(1)

Chứng minh tương tự: CH ⊥ BD (2)

Từ (1) và (2) suy ra H là trực tâm của ∆BCD.

Do đó DH ⊥ BC.

Lại có AH ⊥ BC suy ra BC ⊥ (AHD).

Vậy H là trực tâm của ∆BCD và AD ⊥ BC.

Bài 3 trang 55 SBT Toán 11 Tập 2: Cho tứ diện ABCD có DA ⊥ (ABC), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ AH ⊥ MD tại H.

a) Chứng minh rằng AH ⊥ (BCD).

b) Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Chứng minh rằng GK ⊥ (ABC).

Lời giải:

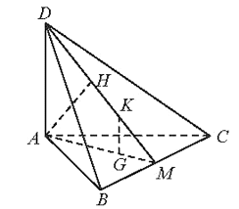
a)Tam giác ABC cân tại A $\Rightarrow$ Trung tuyến AM ⊥ BC.

Lại có DA ⊥ (ABC) $\Rightarrow$ DA ⊥ BC.

$\Rightarrow$ BC ⊥ (ADM) $\iff$ BC ⊥ AH. (1)

Theo giả thiết: AH ⊥ DM. (2)

Từ (1) và (2) suy ra AH ⊥ (BCD).

b)Ta có: $\frac{MK}{MD}=\frac{MG}{MA}=\frac{1}{3}$ nên GK // AD (theo định lí Thalès).

Ta lại có AD ⊥ (ABC) suy ra GK ⊥ (ABC).

Bài 4 trang 55 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình thoi, O là giao điểm của hai đường chéo, SA = SC, SB = SD.

a) Chứng minh rằng SO ⊥ (ABCD).

b) Gọi I, J lần lượt là trung điểm của BA, BC. Chứng minh rằng IJ ⊥ (SBD).

c) Chứng minh rằng BD ⊥ (SAC).

Lời giải:

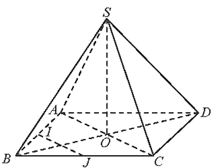
a)Từ giả thiết, dễ dàng nhận thấy ∆SAC và ∆SBD là các tam giác cân.

Ta có: 

Do đó SO ⊥ (ABCD)

b)Ta có AC ⊥ BD và AC ⊥ SO, suy ra AC ⊥ (SBD).

IJ là đường trung bình của ∆ABC nên IJ // AC.

Do đó IJ ⊥ (SBD).

c)Ta có BD ⊥ AC (ABCD là hình thoi) và BD ⊥ SO, suy ra BD ⊥ (SAC).

=============
THUỘC: Giải SÁCH bài tập Toán 11 – CTST