Giải Sách bài tập Toán 11 Bài 2: Các quy tắc tính đạo hàm – SÁCH GIÁO KHOA CHÂN TRỜI SÁNG TẠO 2024
================
Giải SBT Toán 11 Bài 2: Các quy tắc tính đạo hàm
Giải SBT Toán 11 trang 43
Bài 1 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) ;
b) y = (x2 − 1)(x2 – 4)(x2 + 9);
c) ;
d) ;
e) y = xe2x + 1;
g) y = (2x + 3)32x + 1;
h) y = xln2x;
i) .
Lời giải:
a) .
b) y = (x2 − 1)(x2 – 4)(x2 + 9)
= (x4 – 5x2 + 4)(x2 + 9)
= x6 – 5x4 + 4x2 + 9x4 – 45x2 + 36
= x6 + 4x4 – 41x2 + 36.
y’ = 6x5 + 16x3 – 82x
c)
.
d)
e)
.
g)
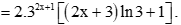
h)
.
i) .
Bài 2 trang 43 SBT Toán 11 Tập 2: Cho hàm số . Tính (a là hằng số khác 0).
Lời giải:
Ta có .
• .
• .
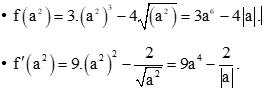
Vậy 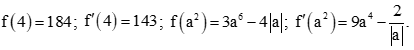
Bài 3 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) y = (1 + x2)20;
b) .
Lời giải:
a) .
b)
.
Bài 4 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) ;
b) ;
c) ;
d) y = cos (2sinx).
Lời giải:
a)
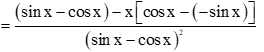
.
b)
c)
.
d)
Bài 5 trang 43 SBT Toán 11 Tập 2: Tính đạo hàm cấp 2 của các hàm số sau:
a) y = xsin 2x;
b) y = cos2x;
c) y = x4 – 3x3 + x2 − 1.
Lời giải:
a)
.
b)
.
c) .
.
Bài 6 trang 43 SBT Toán 11 Tập 2: Một chất điểm chuyển động thẳng có phương trình s = 100 + 2t – t2 trong đó thời gian được tính bằng giây và s được tính bằng mét.
a) Tại thời điểm nào chất điểm có vận tốc bằng 0?
b) Tìm vận tốc và gia tốc của chất điểm tại thời điểm t = 3s.
Lời giải:
Ta có , suy ra .
a) Vận tốc chất điểm bằng 0 khi hay t = 1
Vậy vận tốc chất điểm bằng 0 khi t = 1 s.
b) Khi t = 3s, ta có:
• (m/s);
• (m/s2).
Vậy khi t = 3 s thì vận tốc của chất điểm là −4 m/s; gia tốc của chất điểm là −2 m/s2.
Giải SBT Toán 11 trang 44
Bài 7 trang 44 SBT Toán 11 Tập 2: Một chuyển động thẳng xác định bởi phương trình s(t) = −2t3 + 75t + 3, trong đó s tính bằng mét và t là thời gian tính bằng giây. Tính vận tốc và gia tốc của chuyển động tại thời điểm t =3
Lời giải:
Ta có , suy ra .
• (m/s).
• (m/s2).
Vậy tại thời điểm t = 3 vận tốc của chuyển động là 21 (m/s) và gia tốc của chuyển động là −36 (m/s2).
Bài 8 trang 44 SBT Toán 11 Tập 2: Nếu số lượng sản phẩm sản xuất được của một nhà máy là x (đơn vị: trăm sản phẩm) thì lợi nhuận sinh ra là P(x) = 200(x – 2)(17 – x) (nghìn đồng). Tính tốc độ thay đổi lợi nhuận của nhà máy đó khi sản xuất 3000 sản phẩm
Lời giải:
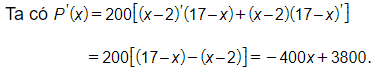
Vậy tốc độ thay đổi lợi nhuận của nhà máy đó khi sản xuất 3000 sản phẩm là –8200 nghìn đồng.
=============
THUỘC: Giải SÁCH bài tập Toán 11 – CTST
