Giải bài tập Toán 9 Bài 3 (Chân trời sáng tạo): Góc ở tâm, góc nội tiếp

Giải chi tiết Giải bài tập Toán 9 Bài 3 (Chân trời sáng tạo): Góc ở tâm, góc nội tiếp – SÁCH GIÁO KHOA TOÁN 9 CHÂN TRỜI SÁNG TẠO – 2024

================

Giải bài tập Toán 9 Bài 3: Góc ở tâm, góc nội tiếp

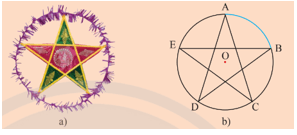
Khởi động trang 90 Toán 9 Tập 1:Hình ngôi sao năm cánh trong Hình a được vẽ lại như Hình b. Phần tô màu xanh trên đường tròn từ điểm A đến điểm B được gọi là gì? Làm thế nào để biểu diễn số đo của nó?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Phần tô màu xanh trên đường tròn từ điểm A đến điểm B được gọi là cung nhỏ AB.

Để biểu diễn được số đo của cung nhỏ AB, ta cần tính số đo góc ở tâm$\widehat{AOB}.$

Xét đường tròn (O), có 5 góc ở tâm bằng nhau là$\widehat{AOB},\widehat{BOC},\widehat{COD},\widehat{DOE},\widehat{EOA}.$

Do đó:$\widehat{AOB}=\frac{1}{5}\cdot 360°=72°.$

Vậy$sđ\stackrel{⏜}{AB}=72°.$

1. Góc ở tâm

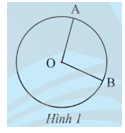
Khám phá 1 trang 90 Toán 9 Tập 1:Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của$\widehat{AOB}.$

Lời giải:

Xét$\widehat{AOB},$có:

⦁ Đỉnh là O, trùng với tâm của đường tròn (O; R);

⦁ Hai cạnh là OA, OB là bán kính của đường tròn (O; R).

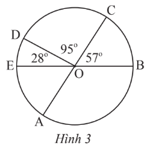
Thực hành 1 trang 90 Toán 9 Tập 1:Tính số đo góc ở tâm$\widehat{EOA}$và$\widehat{AOB}$trong Hình 3. Biết AC và BE là hai đường kính của đường tròn (O).

Lời giải:

Xét đường tròn (O):

⦁$\widehat{EOA}=\widehat{BOC}=57°$(đối đỉnh);

⦁$\widehat{AOB}=\widehat{COE}=\widehat{COD}+\widehat{DOE}=95°+28°=123°.$

Vận dụng 1 trang 91 Toán 9 Tập 1:Tính số đo góc ở tâm được tạo thành khi kim giờ quay:

a) Từ 7 giờ đến 9 giờ;

b) Từ 9 giờ đến 12 giờ.

Lời giải:

Sau 12 giờ, kim giờ sẽ quay được một vòng, ứng với 360°.

Mỗi giờ kim giờ quay được một góc ở tâm có số đo là$\frac{360°}{12}=30°.$

a) Từ 7 giờ đến 9 giờ, kim giờ quay một góc ở tâm có số đo là:$\left(9-7\right)\cdot 30°=60°.$

b) Từ 9 giờ đến 12 giờ, kim giờ quay một góc ở tâm có số đo là:$\left(12-9\right)\cdot 30°=90°.$

2. Cung, số đo cung

Khám phá 2 trang 91 Toán 9 Tập 1:Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được phân chia bởi hai điểm A và B.

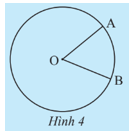
Lời giải:

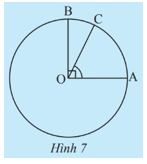
Khám phá 3 trang 91 Toán 9 Tập 1:Cho OA và OB là hai bán kính vuông góc với nhau của đường tròn (O), C là điểm trên cung nhỏ AB (Hình 7). Ta coi số đo của một cung nhỏ là số đo của góc ở tâm chắn cung đó.

a) Xác định số đo của cung AB.

b) So sánh số đo của hai cung$\stackrel{⏜}{AC}$và$\stackrel{⏜}{AB}.$

Lời giải:

a) Số đo của cung AB là số đo của$\widehat{AOB}$và bằng 90°.

b) Ta có số đo của cung AC là số đo của$\widehat{AOC}.$

Mà$\widehat{AOC}<\widehat{AOB}$nên số đo của cung AC nhỏ hơn số đo của cung AB.

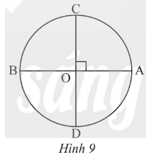
Thực hành 2 trang 92 Toán 9 Tập 1:Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau (Hình 9). Xác định số đo của các cung$\stackrel{⏜}{AB},\stackrel{⏜}{AC}$và$\stackrel{⏜}{AD}.$

Lời giải:

Vì AB là đường kính nên cung AB là cung nửa đường tròn, do đó

$sđ\stackrel{⏜}{AB}=180°.$

Vì AB và CD là hai đường kính vuông góc với nhau nên$\widehat{AOC}=\widehat{AOD}=90°.$

Do đó$sđ\stackrel{⏜}{AC}=\widehat{AOC}=90°;sđ\stackrel{⏜}{AD}=\widehat{AOD}=90°.$

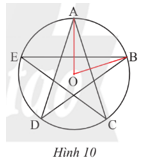
Vận dụng 2 trang 92 Toán 9 Tập 1:Xác định số đo cung AB trong hình ngôi sao năm cánh (Hình 10).

Lời giải:

Xét đường tròn (O), có 5 góc ở tâm bằng nhau là$\widehat{AOB},\widehat{BOC},\widehat{COD},\widehat{DOE},\widehat{EOA}.$

Do đó:$\widehat{AOB}=\frac{1}{5}\cdot 360°=72°.$

Vậy$sđ\stackrel{⏜}{AB}=72°.$

Khám phá 4 trang 92 Toán 9 Tập 1:Trên đường tròn (O), vẽ hai cung nhỏ$\stackrel{⏜}{AB},\stackrel{⏜}{BC}$sao cho$\widehat{AOB}=18°,\widehat{BOC}=32°$và tia OB ở giữa hai tia OA, OC (Hình 11). Tính số đo của các cung$\stackrel{⏜}{AB},\stackrel{⏜}{BC},\stackrel{⏜}{AC}.$

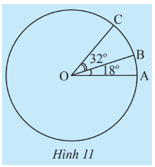
Lời giải:

Xét đường tròn (O), ta có:

⦁$sđ\stackrel{⏜}{AB}=\widehat{AOB}=18°;$

⦁$sđ\stackrel{⏜}{BC}=\widehat{BOC}=32°;$

⦁$sđ\stackrel{⏜}{BC}=\widehat{AOC}=\widehat{AOB}+\widehat{BOC}=18°+32°=50°.$

Thực hành 3 trang 93 Toán 9 Tập 1:Trên cung AB có số đo 90° của đường tròn (O), lấy điểm M sao cho cung AM có số đo 15°. Tính số đo của cung MB.

Lời giải:

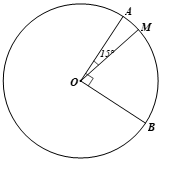
Xét đường tròn (O), ta có:$sđ\stackrel{⏜}{AB}=sđ\stackrel{⏜}{AM}+sđ\stackrel{⏜}{MB}$

Suy ra$sđ\stackrel{⏜}{MB}=sđ\stackrel{⏜}{AB}-sđ\stackrel{⏜}{AM}=90°-15°=75°.$

Vận dụng 3 trang 93 Toán 9 Tập 1:Bạn Hùng làm một cái diều với thân diều là hình tứ giác SAOB sao cho OS là đường phân giác của$\widehat{AOB}$và$\widehat{ASB}=106°.$Thanh tre màu xanh lá được uốn cong thành cung AB của đường tròn tâm O và SA, SB là hai tiếp tuyến của (O), (Hình 12). Tính số đo của$\stackrel{⏜}{AB}.$

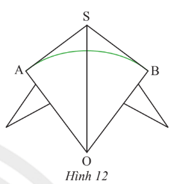
Lời giải:

Vì SA, SB lần lượt là hai tiếp tuyến của (O) tại A, B nên SA ⊥ OA tại A và SB ⊥ OB hay$\widehat{SAO}=\widehat{SBO}=90°.$

Xét tứ giác SAOB có:$\widehat{SAO}+\widehat{AOB}+\widehat{SBO}+\widehat{ASB}=360°$(tổng các góc của một tam giác).

Suy ra$\widehat{AOB}=360°-\left(\widehat{SAO}+\widehat{SBO}+\widehat{ASB}\right)$

Do đó$\widehat{AOB}=360°-\left(90°+90°+106°\right)=360°-286°=74°.$

3. Góc nội tiếp

Khám phá 5 trang 93 Toán 9 Tập 1:Quan sát Hình 13. Hãy cho biết trong các góc$\widehat{APB},\widehat{AOB},\widehat{AMB},\widehat{AQB},$góc nào có đỉnh nằm trên đường tròn (O).

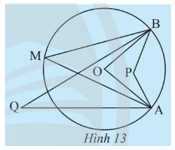
Lời giải:

Trong các góc$\widehat{APB},\widehat{AOB},\widehat{AMB},\widehat{AQB},$góc có đỉnh nằm trên đường tròn (O) là$\widehat{AMB}.$

Thực hành 4 trang 93 Toán 9 Tập 1:Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội tiếp của đường tròn (I) và tính số đo của các góc nội tiếp đó.

Lời giải:

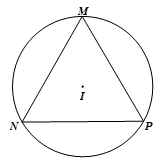
Xét đường tròn (I), ta có các góc nội tiếp đường tròn là:$\widehat{MNP},\widehat{NPM},\widehat{PMN}.$

Vì ∆MNP là tam giác đều nên$\widehat{MNP}=\widehat{NPM}=\widehat{PMN}=60°.$

Vận dụng 4 trang 93 Toán 9 Tập 1:Cho hai điểm E và F nằm trên đường tròn (O). Có bao nhiêu góc nội tiếp chắn cung EF?

Lời giải:

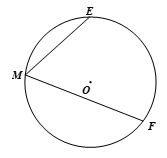
Có vô số góc nội tiếp chắn cung EF vì với mỗi điểm M (khác E và F) nằm trên đường tròn (O) thì ta có một góc nội tiếp.

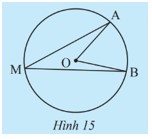
Khám phá 6 trang 94 Toán 9 Tập 1:Quan sát Hình 15. Ta có góc nội tiếp$\widehat{AMB}$chắn cung AB trên đường tròn (O). Cho biết$\widehat{AOB}=60°.$

a) Tính số đo$\stackrel{⏜}{AB}.$

b) Dùng thước đo góc để tìm số đo$\widehat{AMB}.$

c) Có nhận xét gì về hai số đo của$\widehat{AMB}$và$\stackrel{⏜}{AB}?$

Lời giải:

a) Ta có$sđ\stackrel{⏜}{AB}=\widehat{AOB}=60°.$

b) Dùng thước đo góc, ta đo được$\widehat{AMB}=30°.$

c) Nhận xét:$\widehat{AMB}=\frac{1}{2}sđ\stackrel{⏜}{AB}.$

Thực hành 5 trang 96 Toán 9 Tập 1:Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho$\widehat{AOB}=50°,$$\widehat{BOC}=30°,$điểm B thuộc cung nhỏ AC. Gọi M, N lần lượt là hai điểm trên hai cung nhỏ$\stackrel{⏜}{AB},\stackrel{⏜}{AC}$và chia mỗi cung đó thành hai cung bằng nhau. Tìm số đo các góc sau:

a)$\widehat{BCA},\widehat{BAC};$

b)$\widehat{MBA},\widehat{BAN}.$

Lời giải:

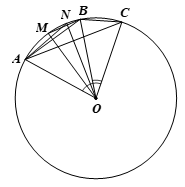
a) Xét đường tròn (O), ta có:

⦁$\widehat{BCA}$và$\widehat{BOA}$lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AB nên$\widehat{BCA}=\frac{1}{2}\widehat{BOA}=\frac{1}{2}\cdot 50°=25°.$

⦁$\widehat{BCA}$và$\widehat{BOC}$lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BC nên$\widehat{BAC}=\frac{1}{2}\widehat{BOC}=\frac{1}{2}\cdot 30°=15°.$

b) Xét đường tròn (O), ta có điểm B thuộc cung nhỏ AC nên:

$sđ\stackrel{⏜}{AC}=sđ\stackrel{⏜}{AB}+sđ\stackrel{⏜}{BC}=\widehat{AOB}+\widehat{BOC}=50°+30°=80°.$

Vì M, N lần lượt chia$\stackrel{⏜}{AB},\stackrel{⏜}{AC}$thành hai cung bằng nhau nên:

⦁$sđ\stackrel{⏜}{AM}=\frac{1}{2}sđ\stackrel{⏜}{AB}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}\cdot 50°=25°;$

⦁$sđ\stackrel{⏜}{NC}=\frac{1}{2}sđ\stackrel{⏜}{AC}=\frac{1}{2}\widehat{AOC}=\frac{1}{2}\cdot 80°=40°.$

Ta có: điểm B thuộc cung nhỏ CN nên:$sđ\stackrel{⏜}{NC}=sđ\stackrel{⏜}{BN}+sđ\stackrel{⏜}{BC}$

Suy ra$sđ\stackrel{⏜}{BN}=sđ\stackrel{⏜}{NC}-sđ\stackrel{⏜}{BC}=40°-30°=10°.$

Ta có:

⦁$\widehat{MBA}$là góc nội tiếp chắn cung AM nên$\widehat{MBA}=\frac{1}{2}sđ\stackrel{⏜}{AM}=\frac{1}{2}\cdot 25°=\mathrm{12,5}°;$

⦁$\widehat{BAN}$là góc nội tiếp chắn cung BN nên$\widehat{BAN}=\frac{1}{2}sđ\stackrel{⏜}{BN}=\frac{1}{2}\cdot 10°=5°.$

Vận dụng 5 trang 96 Toán 9 Tập 1:Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn MN (Hình 20). Nếu bóng được đặt ở điểm X thì$\widehat{MXN}$gọi là góc sút từ vị trí X. Hãy so sánh các góc sút$\widehat{MXN},\widehat{MYN},\widehat{MZN}.$

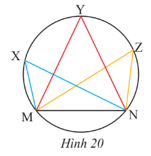
Lời giải:

Xét đường tròn chứa cung MN, ta có$\widehat{MXN},\widehat{MYN},\widehat{MZN}$là các góc nội tiếp chắn cung MN nên$\widehat{MXN}=\widehat{MYN}=\widehat{MZN}.$

Vậy các góc sút$\widehat{MXN},\widehat{MYN},\widehat{MZN}$bằng nhau.

Bài tập

Bài 1 trang 97 Toán 9 Tập 1:Cho đường tròn (O; 5 cm) và điểm M sao cho OM = 10 cm. Qua M vẽ hai tiếp tuyến với đường tròn tại A và B. Tính số đo góc ở tâm được tạo bởi hai tia OA và OB.

Lời giải:

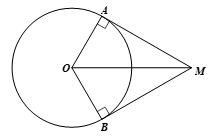
Xét đường tròn (O; 5 cm), ta có: MA, MB lần lượt là tiếp tuyến tại A, B của (O) nên MA ⊥ OA tại A (tính chất tiếp tuyến) và OM là tia phân giác của$\widehat{AOB}$(tính chất hai tiếp tuyến cắt nhau).

Xét ∆OAM vuông tại A, ta có:$\cos \widehat{AOM}=\frac{OA}{OM}=\frac{5}{10}=\frac{1}{2}.$

Suy ra$\stackrel{⏜}{AOM}={60}^0$

Do đó$\widehat{AOB}=2\widehat{AOM}=2\cdot 60°=120°$(do OM là tia phân giác của$\widehat{AOB}$

Vậy số đo góc ở tâm được tạo bởi hai tia OA và OB là$\widehat{AOB}$= 120⁰

Bài 2 trang 97 Toán 9 Tập 1:Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung$\stackrel{⏜}{BD},\stackrel{⏜}{DE},\stackrel{⏜}{EC}.$

Lời giải:

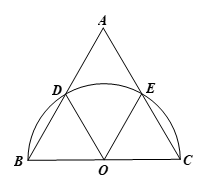
Gọi O là trung điểm của BC. Khi đó ta có đường tròn (O) đường kính BC chứa các cung BD, DE, EC.

Vì ∆ABC là tam giác đều nên$\widehat{ABC}=\widehat{ACB}=60°.$

Xét ∆OBD có OB = OD (cùng bằng bán kính đường tròn (O) đường kính BC) nên ∆OBD cân tại O.

Lại có$\widehat{DBO}=60°$nên ∆OBD là tam giác đều, suy ra$\widehat{BOD}=60°.$Khi đó$sđ\stackrel{⏜}{BD}=60°.$(1)

Tương tự, ta cũng có ∆OCE là tam giác đều, suy ra$\widehat{COE}=60°.$Khi đó$sđ\stackrel{⏜}{CE}=60°.$(2)

Ta có BC là đường kính của đường tròn nên$\widehat{BOC}=sđ\stackrel{⏜}{BC}=180°.$

Có$\widehat{BOC}=\widehat{BOD}+\widehat{DOE}+\widehat{COE}$

Suy ra$\widehat{DOE}=\widehat{BOC}-\left(\widehat{BOD}+\widehat{COE}\right)$

Do đó$\widehat{DOE}=180°-\left(60°+60°\right)=60°.$Khi đó$sđ\stackrel{⏜}{DE}=60°.$(3)

Từ (1), (2) và (3) ta có:$sđ\stackrel{⏜}{BD}=sđ\stackrel{⏜}{DE}=sđ\stackrel{⏜}{CE}\left(=60°\right).$

Do đó các cung BD, DE, EC bằng nhau.

Bài 3 trang 97 Toán 9 Tập 1:Dây cung AB chia đường tròn (O) thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ.

a) Tính số đo mỗi cung.

b) Chứng minh khoảng cách OH từ tâm O đến dây cung AB có độ dài bằng$\frac{AB}{2}.$

Lời giải:

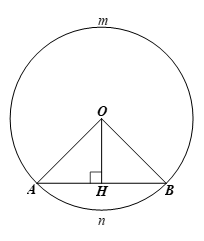
a) Gọi$\stackrel{⏜}{AmB}$và$\stackrel{⏜}{AnB}$lần lượt là cung lớn và cung nhỏ AB.

Theo bài, ta có:$sđ\stackrel{⏜}{AmB}=3sđ\stackrel{⏜}{AnB}.$

Mà$sđ\stackrel{⏜}{AmB}+\stackrel{⏜}{AnB}=360°$

Nên$sđ\stackrel{⏜}{AnB}+3sđ\stackrel{⏜}{AnB}=360°$

Hay$4sđ\stackrel{⏜}{AnB}=360°,$suy ra$sđ\stackrel{⏜}{AnB}=90°.$

Do đó$sđ\stackrel{⏜}{AmB}=3sđ\stackrel{⏜}{AnB}=3\cdot 90°=270°.$

b) Xét ∆OAB có OA = OB (cùng bằng bán kính của đường tròn (O)) nên ∆OAB cân tại O.

Do đó đường cao OH đồng thời là đường trung tuyến của tam giác.

Lại có$sđ\stackrel{⏜}{AnB}=90°$(câu a) nên$\widehat{AOB}=90°.$

Khi đó ∆OAB vuông tại O có OH là đường trung tuyến ứng với cạnh huyền AB nên$OH=\frac{AB}{2}.$

Bài 4 trang 97 Toán 9 Tập 1:Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu vào những thời điểm sau?

a) 2 giờ;

b) 8 giờ;

c) 21 giờ.

Lời giải:

Góc ở tâm tạo bởi hai kim giữa hai số liền nhau là: 360° : 12 = 30°.

a) Vào thời điểm 2 giờ (kim giờ chỉ số 2, kim phút chỉ số 12) thì góc ở tâm tạo thành giữa hai kim đồng hồ là:

2 . 30° = 60°.

b) Vào thời điểm 8 giờ (kim giờ chỉ số 8, kim phút chỉ số 12) thì góc ở tâm tạo thành giữa hai kim đồng hồ là:

4 . 30° = 120°.

c) Vào thời điểm 21 giờ (kim giờ chỉ số 9, kim phút chỉ số 12) thì góc ở tâm tạo thành giữa hai kim đồng hồ là:

3 . 30° = 90°.

Bài 5 trang 97 Toán 9 Tập 1:Cho hai đường tròn đồng tâm (O; R) và$\left(O;\frac{R\sqrt{3}}{2}\right).$Một tiếp tuyến của đường tròn nhỏ cắt đường tròn lớn tại hai điểm A và B. Tính số đo cung AB.

Lời giải:

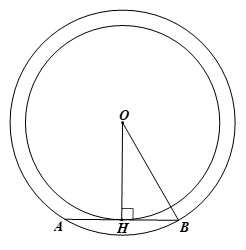
Gọi H là tiếp điểm của tiếp tuyến của đường tròn nhỏ.

Khi đó, ta có OH ⊥ AB tại H và$OH=\frac{R\sqrt{3}}{2}.$

Xét ∆OHB vuông tại H, ta có:$\cos \widehat{HOB}=\frac{OH}{OB}=\frac{}{}\frac{R\sqrt{3}}{2}R=\frac{\sqrt{3}}{2}.$

Do đó$\widehat{HOB}=30°.$

Xét ∆OAB có OA = OB nên ∆OAB cân tại O, do đó đường cao OH đồng thời là đường phân giác của tam giác,

Suy ra$\widehat{AOB}=2\widehat{HOB}=2\cdot 30°=60°.$

Vậy$sđ\stackrel{⏜}{AB}=\widehat{AOB}=60°.$

Bài 6 trang 97 Toán 9 Tập 1:Xác định số đo các cung$\stackrel{⏜}{AB},\stackrel{⏜}{BC},\stackrel{⏜}{CA}$trong mỗi hình vẽ sau.

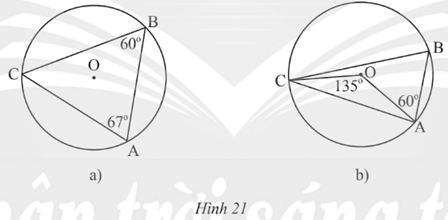
Lời giải:

– Hình 21a):

Xét ∆ABC có$\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$(tổng ba góc của một tam giác).

Suy ra$\widehat{ACB}=180°-\left(\widehat{BAC}+\widehat{ABC}\right)=180°-\left(67°+60°\right)=53°.$

Xét đường tròn (O):

⦁$\widehat{ACB}$là góc nội tiếp chắn cung AB nên$sđ\stackrel{⏜}{AB}=2\widehat{ACB}=2\cdot 53°=106°.$

⦁$\widehat{BAC}$là góc nội tiếp chắn cung BC nên$sđ\stackrel{⏜}{BC}=2\widehat{BAC}=2\cdot 67°=134°.$

⦁$\widehat{ABC}$là góc nội tiếp chắn cung AC nên$sđ\stackrel{⏜}{AC}=2\widehat{ABC}=2\cdot 60°=120°.$

– Hình 21b):

Xét ∆OAB có OA = OB nên ∆OAB cân tại O, lại có$\widehat{OAB}=60°$nên ∆OAB đều. Do đó$\widehat{AOB}=60°.$

Ta có:$\widehat{AOB}+\widehat{BOC}+\widehat{COA}=360°$

Suy ra$\widehat{BOC}=360°-\left(\widehat{AOB}+\widehat{COA}\right)=360°-\left(60°+135°\right)=165°.$

Xét đường tròn (O):

⦁$sđ\stackrel{⏜}{AB}=\widehat{AOB}=60°.$

⦁$sđ\stackrel{⏜}{BC}=2\widehat{BOC}=165°.$

⦁$sđ\stackrel{⏜}{AC}=2\widehat{AOC}=135°.$

Bài 7 trang 97 Toán 9 Tập 1:Cho đường tròn (O) có hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung nhỏ AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng$\widehat{MSD}=2\widehat{MBA}.$

Lời giải:

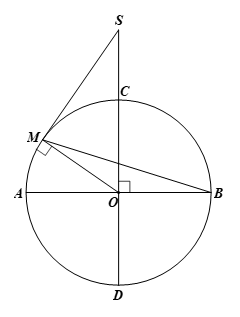
Vì SM là tiếp tuyến của đường tròn (O) tại M nên SM ⊥ OM tại M.

Xét ∆SMO vuông tại M có$\widehat{MSO}+\widehat{MOS}=90°$(1) (tổng hai góc nhọn trong tam giác vuông bằng 90°).

Lại có hai đường kính AB, CD vuông góc với nhau nên AB ⊥ CD tại O, do đó$\widehat{MOA}+\widehat{MOS}=90°$(2)

Từ (1) và (2) suy ra$\widehat{MSO}=\widehat{MOA}.$(3)

Xét đường tròn (O),$\widehat{MOA}$và$\widehat{MBA}$lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung AB. Do đó$\widehat{MBA}=\frac{1}{2}\widehat{MOA}$hay$\widehat{MOA}=2\widehat{MBA}.$(4)

Từ (3) và (4) suy ra$\widehat{MSO}=2\widehat{MBA}$hay$\widehat{MSD}=2\widehat{MBA}.$

Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Bài 2. Tiếp tuyến của đường tròn

Bài 3. Góc ở tâm, góc nội tiếp

Bài 4. Hình quạt tròn và hình vành khuyên

Bài tập cuối chương 5

Hoạt động 1. Làm giác kế đo góc nâng đơn giản

Hoạt động 2. Vẽ đường tròn bằng phần mềm GeoGebra

=============
THUỘC: Giải bài tập Toán 9 – SGK CHÂN TRỜI SÁNG TẠO