Đề bài
A. TRẮC NGHIỆM (3,0 điểm)
Câu 1: Khẳng định nào sau đây sai?
A.cos2a = cos2a – sin2a
B.cos2a = 1 – 2sin2a
C.cos2a= 2cos2a – 1
D.cos2a= 2cosa.sina
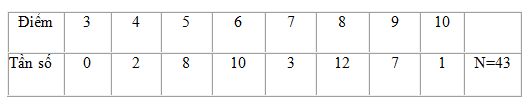
Câu 2: Điều tra về điểm thi môn Toán của 43 học sinh lớp 10A thu được bảng tần số sau:
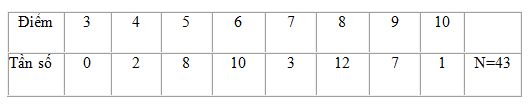
Mốt có giá trị là:
A.M0 = 8 B.M0 = 10
C.M0 = 6 D.M0 = 12
Câu 3: Giá trị nào sau đây bằng cos\(\left( {\alpha + 2017\pi } \right)\)?
A.sin\(\alpha \) B. – sin\(\alpha \)
C.-cos\(\alpha \) D. cos\(\alpha \)
Câu 4: Tập xác định của hàm số y = \(\dfrac{{ – x + 3}}{{\sqrt {{x^2} – 3x – 4} }}\) là:
A.D =(\( – \infty ; – 1) \cup (4; + \infty )\)
B.D = ( – 1;4)
C.D =\(( – \infty ; – 1{\rm{]}} \cup {\rm{[}}4; + \infty )\)
D.D = [ – 1; 4 ]
Câu 5: Bất phương trình x2 – 2mx+ m > 0 ,\(\forall x \in R\) khi :
A.m\( \in \)( – 1; 0)
B.m\( \in \)( 0; 1)
C.m\( \in \)\(( – \infty ; – 1) \cup (0; + \infty )\)
D.m\( \in \)\(( – \infty ; – 1{\rm{]}} \cup {\rm{[}}0; + \infty )\)
Câu 6: Điều tra về điểm thi môn Toán của 43 học sinh lớp 10A thu được bảng tần số sau:
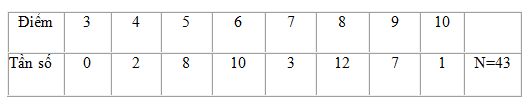
Độ lệch chuẩn của các giá trị là:
A.s = 2,53 B.s = 7
C. s =1,59 D.s = 6
Câu 7: Elip (E): \(\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{4} = 1\) có độ dài trục nhỏ là :
A.6 B.4
C.16 D.8
Câu 8: Đường thẳng d: x + 2y – 1 = 0 song song với đường thẳng có phương trình nào sau đây?
A.x + 2y – 1 = 0
B. – 2x + y +1 = 0
C.2x – y + 3 = 0
D.x + 2y +1 = 0
Câu 9: Đường tròn có phương trình x2 + y2 – 2x – 3 =0 có bán kính là:
A.R = 5 B. R= \(\sqrt {13} \)
C. R =1 D.R = 2
Câu 10: Đường thẳng d: \(\left\{ \begin{array}{l}x = 2 + t\\y = 3 – 2t\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,(t \in R)\), đi qua điểm:
A.A(1; – 2) B.B(3; 1)
C.C (2; 1) D.D(3; – 2)
Câu 11: Hypebol có trục thực bằng 8, tiêu cự bằng 10 thì có phương trình chính tắc là:
A.\(\dfrac{{{x^2}}}{{16}} – \dfrac{{{y^2}}}{9} = 1\)
B.\(\dfrac{{{x^2}}}{{16}} – \dfrac{{{y^2}}}{{25}} = 1\)
C.\(\dfrac{{{x^2}}}{8} – \dfrac{{{y^2}}}{2} = 1\)
D.\(\dfrac{{{x^2}}}{{16}} – \dfrac{{{y^2}}}{4} = 1\)
Câu 12: Parabol: y2 = 12x có đường chuẩn là:
A.x = 2 B.x = -2
C.x = -3 D.x = 3
B. TỰ LUẬN (7,0 điểm)
Bài 1 (2,5 điểm). Giải các phương trình và bất phương trình sau:
a) \(\dfrac{{{x^2} + 5}}{{{x^2} – 6x – 7}} \le 1\)
b) \(\sqrt {{\rm{2}}{{\rm{x}}^{\rm{2}}}{\rm{ – 5x – 2}}} \,\,\, = x – 2\)
c) \(\sqrt {{{\rm{x}}^{\rm{2}}}{\rm{ – 8x }}} \,\,\, \le x – 2\)
Bài 2 (1,0 điểm). Cho hàm số f(x) = \( – {x^2} + 2(m – 2)x + m – 2\). Tìm m để f(x) \( < 0,\,\,\,\,\forall x \in R\).
Bài 3 (1,5 điểm)
a) Cho \(\sin a = \dfrac{1}{3}\), \(\left( {\dfrac{\pi }{2} < a < \pi } \right)\). Tính \(\cos a\) ; \(\cos 2a\) và sin\(2a\).
b) Cho tam giác ABC. Chứng minh rằng: tanA+ tanB+ tanC = tanA.tanB.tanC.
Bài 4 (2,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(1; 0) , B( – 2; 4) , đường thẳng
\(\Delta \): 2x – y + 1 = 0 và đường tròn (C): (x –1 )2 + (y – 2)2 = 8.
a) Viết phương trình tổng quát của đường thẳng AB.
b) Viết phương trình tham số của đường thẳng d đi qua A và vuông góc với đường thẳng \(\Delta \).
c) Viết phương trình đường tròn (C’) có tâm B và tiếp xúc với đường thẳng \(\Delta \).
d) Viết phương trình đường thẳng đi qua M(6 ;1) và tiếp xúc với đường tròn (C).
Lời giải chi tiết
A.TRẮC NGHIỆM (3,0 điểm)
|
1 |
2 |
3 |
4 |
5 |
6 |
|
D |
A |
C |
A |
B |
C |
|
7 |
8 |
9 |
10 |
11 |
12 |
|
B |
D |
D |
B |
A |
C |
B.TỰ LUẬN (7,0 điểm)
Bài 1:
a)
\(\dfrac{{{x^2} + 5}}{{{x^2} – 6x – 7}} \le 1\)\( \Leftrightarrow \dfrac{{6x + 12}}{{{x^2} – 6x – 7}} \le 0\,\) (*)

Tập nghiệmcủa bất phương trình \(S = ( – \infty ; – 2{\rm{]}} \cup ( – 1;7)\)
b) \(\sqrt {{\rm{2}}{{\rm{x}}^{\rm{2}}}{\rm{ – 5x – 2}}} \,\,\, = x – 2\)
\( \Leftrightarrow \left\{ \begin{array}{l}x – 2 \ge 0\\2{x^2} – 5x – 2 = {\left( {x – 2} \right)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\{x^2} – x – 6 = 0\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\\left[ \begin{array}{l}x = – 2\\x = 3\end{array} \right.\end{array} \right. \Leftrightarrow x = 3\)
Vậy phương trình có 1 nghiệm x=3
c) \(\sqrt {{{\rm{x}}^{\rm{2}}}{\rm{ – 8x }}} \,\,\, \le x – 2\)
\(\,\, \Leftrightarrow \left\{ \begin{array}{l}x – 2{\rm{ }} \ge {\rm{0}}\\{x^2} – 8x \ge {\rm{0}}\\{{\rm{x}}^{\rm{2}}} – 8x \le {{\rm{(x – 2)}}^2}\end{array} \right.\)\( \Leftrightarrow \,\,\left\{ \begin{array}{l}x \ge 2{\rm{ }}\\\left[ \begin{array}{l}x \le 0\\x \ge 8\end{array} \right.\\x \ge – 1\end{array} \right. \Leftrightarrow x \ge 8\)
Tập nghiệm S = [8;\( + \infty \))
Bài 2:
f(x) \( < 0,\,\,\,\,\forall x \in R\)\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ‘ < 0\\a < 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} – 3m + 2 < 0\\ – 1 < 0\end{array} \right. \Leftrightarrow 1 < m < 2\)
KL: 1<m<2
Bài 3:
a) +) \({\cos ^2}a = 1 – {\sin ^2}a = 1 – \dfrac{1}{9} = \dfrac{8}{9}\)\( \Rightarrow \cos a = \pm \dfrac{{2\sqrt 2 }}{3}\) Chọn \(\cos a = – \dfrac{{2\sqrt 2 }}{3}\)
+) \(\cos 2a = 1 – 2{\sin ^2}a = 1 – 2.\dfrac{1}{9} = \dfrac{7}{9}\)
+) \(\sin 2a = 2\sin a.\cos a \)\(\,= 2.\dfrac{1}{3}.\left( { – \dfrac{{2\sqrt 2 }}{3}} \right) = – \dfrac{{4\sqrt 2 }}{9}\)
b) \(VT = \tan A + \tan B + \tan C \)
\(= \dfrac{{\sin (A + B)}}{{\cos A.\cos B}} + \dfrac{{\sin C}}{{{\mathop{\rm cosC}\nolimits} }}\)
= \(\dfrac{{sinC[\cos C + \cos A.\cos B]}}{{cosC\cos A.\cos B}}\)
\( = \dfrac{{{\mathop{\rm tanC}\nolimits} [ – \cos (A + B) + \cos A.\cos B]}}{{\cos A.\cos B}}\)
\( = \dfrac{{{\mathop{\rm tanC}\nolimits} [\sin A.\sin B]}}{{\cos A.\cos B}} = VP\)
Bài 4:
a)
+) Đường thẳng AB đi qua A( 1 ;0) và có 1 VTCP là \(\overrightarrow {AB} \)= (-3; 4) => 1VTPT \(\overrightarrow n \)= (4;3)
+) Phương trình tổng quát AB: 4(x – 1) + 3(y – 0) = 0 \( \Leftrightarrow \) 4x + 3y – 4 = 0
b)
+) Đường thẳng \(\Delta \): 2x – y + 1 = 0 có VTPT \({\overrightarrow n _\Delta } = \left( {2; – 1} \right)\)
Đường thẳng d đi qua A và vuông góc với đường thẳng \(\Delta \) nên có VTCP là \({\overrightarrow n _\Delta }\)=(2;-1)
+) Phương trình tham số của đường thẳng d:
\(\left\{ \matrix{
x = 1 + 2t \hfill \cr
y = – t \hfill \cr} \right.\,\,\left( {t \in R} \right)\)
c) Đường tròn (C’) có tâm B và tiếp xúc với đường thẳng \(\Delta \)nên có bán kính R=\(d(B;\Delta ) = \)\(\dfrac{{|2.\left( { – 2} \right) – 4 + 1|}}{{\sqrt {{2^2} + {{\left( { – 1} \right)}^2}} }} = \dfrac{7}{{\sqrt 5 }}\)
Phương trình đường tròn (C’): \({\left( {x{\rm{ }} + 2{\rm{ }}} \right)^2} + {\left( {y{\rm{ }}–{\rm{ }}4} \right)^2} = \dfrac{{49}}{5}\)
d) Đường tròn (C) có tâm I(1 ;2) bán kính R = 2\(\sqrt 2 \)
Gọi VTPT của tiếp tuyến d là \(\overrightarrow n \)= (a;b) (với a2 + b2\( \ne \)0)
+) d qua M(6 ;1) nên phương trình d: ax + by – 6a – b = 0
+) d tiếp xúc với đường tròn (C) nên : d(I ; l) = R
\( \Leftrightarrow \dfrac{{|a + 2b – 6a – b|}}{{\sqrt {{a^2} + {b^2}} }} = 2\sqrt 2 \)\( \Leftrightarrow 17{a^2} – 10ab – 7{b^2} = 0\)\( \Leftrightarrow \left[ \begin{array}{l}a = b\\a = – \dfrac{{7b}}{{17}}\end{array} \right.\)
+ Với a = b: Chọn a=1 => b= 1 : pt đường d: \(x+ y – 7 = 0\)
+ Với \(a = – \dfrac{{7b}}{{17}}\) : Chọn \(a = 7; b = -17 \)
Phương trình đường d: \(7x – 17 y – 25 = 0\)
