A. Tổng quan kiến thức
Những phép dựng hình cơ bản sau:
- Dựng một đoạn thẳng bằng một đoạn thẳng cho trước.
- Dựng một góc bằng một góc cho trước.
- Dựng đường trung trực của một đoạn thẳng cho trước ,dựng trung điểm của một đoạn thẳng cho trước.
- Dựng tia phân giác của một góc cho trước .
- Qua một điểm cho trước ,dựng một đường thẳng vuông góc với một đường thẳng cho trước .
- Qua một điểm nằm ngoài đường thẳng cho trước ,dựng đường thẳng song song với đường thẳng ấy .
- Vận dụng các phép dựng hình cơ bản để dựng tam giác biết ba cạnh ,hoặc biết hai cạnh và góc xen giữa,hoặc biết một cạnh và góc kề.
Với bài toán dựng hình phức tạp hơn,ta phải tuân thủ các bước của phương pháp dựng hình sau:
- Bước 1: Phân tích hình.
- Bước 2: Dựng hình.
- Bước 3: Chứng minh cách dựng trên thoả mãn yêu cầu của đề toán.
- Bước 4 :Biện luận: Xem lại từng phép dựng đã thực hiện để xem có điều kiện ràng buộc không.Từ đó suy ra bài toán có mấy nghiệm hình.
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
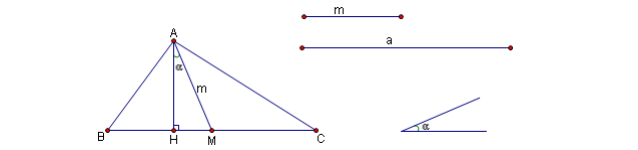
Bài 1: Dựng tam giác ABC ,biết cạnh BC = a ,trung tuyến AM = m (a và m là những độ dài cho trước ) và góc $\alpha $ giữa AM và đường cao AH.

Phân tích :
Giả sử bài toán đã giải xong,và ta đã dựng được tam giác ABC thoả mãn yêu cầu của đề toán .Phân tích hình đó theo hướng phát hiện một bộ phận của hình hội đủ các điều kiện để dựng được một cách chính xác:
- Đó là tam giác vuông AHM có cạnh huyền AM = m
- $\widehat{HAM}=\alpha $ cho trước.
=> Tam giác đó hoàn toàn xác định nên dựng được. Sau khi dựng xong tam giác vuông AHM ,ta hoàn tất hình phải dựng .
Cách dựng hình :
- Dựng đoạn thẳng AM có độ dài m cho trước ( phép dựng cơ bản 1 ).
- Dựng $\widehat{MAx}=\alpha $ cho trước ( phép dựng cơ bản 2 ).
- Từ M kẻ $MH\perp Ax $ tại H ( phép dựng cơ bản 5 ).
- Bây giờ chỉ còn dựng hai đỉnh B,C .Cạnh BC nằm trên đường thẳng MH ,nên trên đường thẳng MH ,ta lấy ở hai phía khác nhau đối với điểm M hai điểmB và C sao cho MB = MC = $\frac{a}{2} $ ( phép dựng cơ bản 3 và 1 ).
Chứng minh :
Rõ ràng tam giác trên đây thoả mãn đầy đủ các yêu cầu của đề toán :
- cạnh BC = a cho trước.
- trung tuyến AM = m cho trước .
- $\widehat{HAM}=\alpha $ cho trước .
Biện luận :
Xét từng bước dựng hình , bước nào cũng được thực hiện rõ ràng, mạch lạc.Duy chỉ có góc $\alpha $ cho trước và yêu cầu đề ra là $\widehat{MAH} $ của tam giác vuông AMH phải bằng $\alpha $ ,thì rõ ràng $\alpha $ phải là góc nhọn .Vậy với điều kiện này thì bài toán bao giờ cũng giải được và có một nghiệm hình .
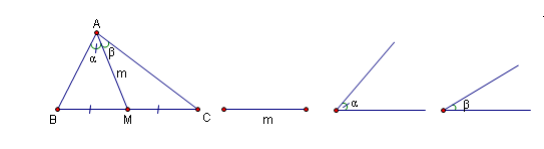
Bài 2: Dựng tam giác ABC với trung tuyến AM có độ dài bằng một đoạn thẳng m cho trước ,và các góc MAB và MAC lần lượt bằng những góc $\alpha $ và $\beta $ cho trước.
Phân tích :
Giả sử bài toán đã giải xong và ta đã dựng được tam giác ABC thoả mãn yêu cầu bài toán .Hình vẽ trên cho thấy không có một bộ phận nào của hình hội đủ điều kiện để dựng được.
Ví dụ: Tam giác AMC chỉ có hai yếu tố được biết là $\widehat{MAC} =\beta $ và AM = m ,nên không thể dựng được.Khi này nhớ lại những bài toán tương tự .
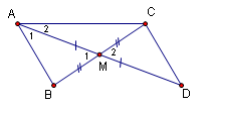
Bài toán :nếu kéo dài trung tuyến AM thêm một đoạn MD = AM ,thì hai tam giác AMB và DMC bằng nhau (c.g.c) .
=> $\widehat{A_{1}} =\widehat{D} $ .
=> Từ đó ,hình thành tam giác ACD với $\widehat{A_{2}} =\beta ,\widehat{D}=\widehat{A_{1}}=\alpha $ và AD = 2m. Tam giác đó hội đủ điều kiện để dựng được .
Sau khi dựng được tam giác này ,ta sẽ dựng được điểm B .
Cách dựng hình :
- Dựng đoạn thẳng AD = 2m.
- Dựng hai góc kề cạnh đó là $\widehat{DAC} =\beta ,\widehat{ADC}=\alpha $ , hai cạnh AC và DC giao nhau tại C.
- Sau đó ta vẽ trung tuyến CA của tam giác ACD và kéo dài thêm một đoạn MB =MC , từ đó xác định đỉnh B của tam giác ABC cần dựng .
Chứng minh :
Theo cách dựng này ,rõ ràng tam giác AMB và tam giác DMC bằng nhau(c.g.c).
Nên ta có :
- $AM=\frac{AD}{2}=m$
- $\widehat{A_{2}} =\beta ,\widehat{A_{1}}=\widehat{d}=\alpha $.
Vậy tam giác ABC dựng được thoả mãn đầy đủ các yêu cầu đề bài .
Biện luận :
Trên đây ta nói hai cạnh AC và DC giao nhau tại C.Thực ra là chúng chỉ giao nhau nếu $\alpha+\beta < 2v $ .
Do đó bài toán luôn giải được và có một nghiệm hình.
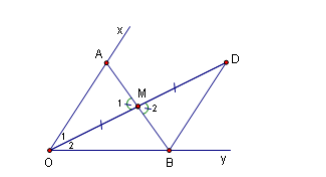
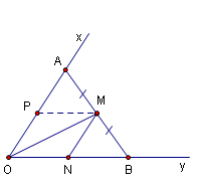
Bài 3: Cho một góc xOy và một điểm M ở bên trong góc ấy .Dựng một đoạn thẳng AB sao cho $A\in Qx, B\in Oy$ và M là trung điểm của AB.
Phân tích bài toán :
Giả sử bài toán giải xong và ta đã dựng được đoạn thẳng AB thoả mãn yêu cầu của đề bài là $A\in Qx, B\in Oy$ và M là trung điểm của AB.
Nếu kéo dài OM thêm đoạn MD = OM thì $\triangle AMO = \triangle BMD$ (c.g.c)
=> $\widehat{O_{1}}=\widehat{D}$
Từ đó , DB // Ox .
Ngược lại, nếu từ D kẻ DB // Ox ( $B\in Oy$) ,rồi BM đến cắt Ox tại A thì $\triangle AMO = \triangle BMD$ (g.c.g)$ với :
- $\widehat{M_{1}}=\widehat{M_{2}}$ (đối đỉnh)
- $\widehat{M_{1}}=\widehat{D}$ (so le trong ,DB // Ox)
- MD = OM (do dựng )
=> AM = MB.
Cách dựng hình :
Kéo dài OM thêm đoạn MD= OM ,rồi từ D kẻ đường thẳng // Ox ,cắt Oy tại B.
Tiếp đến kẻ BM cho đến cắt Ox tại A thì M là trung điểm của AB.
Chứng minh:
Xét $\triangle AMO$ và $\triangle BMD$ có :
- $\widehat{M_{1}}=\widehat{M_{2}}$ (đối đỉnh)
- MD = OM (do dựng )
- $\widehat{O_{1}}=\widehat{MDB}$ (so le trong ,DB // Ox)
=> $\triangle AMO = \triangle BMD$ (g.c.g)$
=> AM = MD .
Biện luận :
Bài toán luôn có một nghiệm.
* Bài toán có thể phân tích cách khác : Kéo MN // Ox ( $N\in Oy$ ) => MN= 2 OA .
Ngược lại, nếu kẻ MN // Ox ( $N\in Oy$ ),và lấy điểm A trên Ox sao cho OA = 2MN ,rồi kẻ AM đến cắt Oy tại B thì có AM =MB.
Quả vậy ,gọi B là trung điểm của OA => OP = PA => PM // ON.
Vậy BM phải đi qua trung điểm của AB,tức AM = MB .
Qua phân tích này ta thấy rõ cách dựng và chứng minh .
Vậy bài toán luôn có một nghiệm.
Bài 4: Cho một góc xOy và hai điểm A , B .Dựng một điểm cách đều hai cạnh Ox,Oy và cách đều hai điểm A , B.
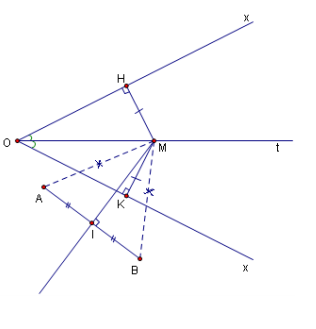
Phân tích bài toán :
Giả sử bài toán đã giải xong và ta đã dựng được điểm M cách đều hai cạnh Ox, Oy và cách đều hai điểm A,B
Nghĩa là có MH = MK ($MH \perp Ox,H \in Ox, MK \perp Oy,K \in Oy$) và MA=MB.
Vậy M vưà thuộc tia phân giác Ot của xOy, vừa thuộc đường trung trực d của AB nên M là giao điểm của Ot và d .
Cách dựng hình :
Dựng tia phân giác Ot của góc xOy và đường trung trực d của AB ,d cắt Ot tại M.
=> M là điểm cần dựng.
Chứng minh:
Ta có :
- $M \in Ot$ nên MH = MK .
- $M \in d$ nên MA = MB.
Biện luận :
Ta có :
- d cắt Ot nếu AB không vuông góc với Ot => Bài toán có một nghiệm hình .
- Nếu $AB \perp Ot $ và $OA \neq OB $ thì Ot // d => Bài toán vô nghiệm.
- Nếu $AB \perp Ot $ và OA = OB thì $d \equiv Ot $ => Bài toán có vô số nghiệm,nghĩa là bất kỳ điểm nào của Ot cũng vừa cách đều hai cạnh Ox và Oy,vừa cách đều A và B.
Bài 5: Cho một góc nhọn xOy và một điểm A trên Oy.Tìm một điểm M trên đoạn OA sao cho nếu kẻ MP = MA.
Phân tích bài toán :
Giả sử bài toán đã giải xong và ta đã dựng được điểm M theo yêu cầu của đề bài.
Kẻ PN // AM và PN = AM => AN // NP , Có nghĩa là $ AN Ox\perp $ (1)
Mặt khác PN = AM = OP nên tam giác OPN cân : $\widehat{O_{1}}=\widehat{N_{1}}$
Mà $\widehat{O_{2}}=\widehat{N_{1}}$ (góc so le trong PN // Oy) => $\widehat{O_{1}}=\widehat{O_{2}}$.
Điều đó có nghĩa là N nằm trên tia phân giác của góc xOy .
Theo (1) thì N nằm trên đường thẳng vuông góc với Ox hạ từ A.Vậy N là giao điểm của đường thẳng đó với tia phân giác của góc xOy . Vị trí N hoàn toàn xác định => do đó dựng được hình theo yêu cầu.
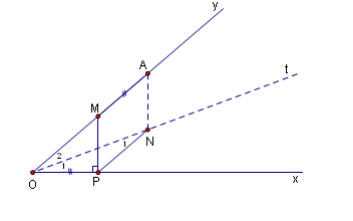
Cách dựng hình :
Kẻ tia phân giác Ot của góc xOy và từ A ,kẻ đường thẳng vuông góc với Ox , cắt Ot tại N .
Từ N kẻ NP // Oy ,cắt Ox tại P .Từ P kẻ đường thẳng vuông góc với Ox, cắt Oy tại điểm N cần dựng .
Chứng minh :
Ta có :
NP // Oy nên $\widehat{O_{2}}=\widehat{N_{1}}$ (so le trong )
Mà Ot là tia phân giác : $\widehat{O_{1}}=\widehat{O_{2}}$.
=> $\widehat{O_{1}}=\widehat{N_{1}}$
=> Tam giác OPN cân tại P : OP = PN.
Mà MP và AN cùng vuông góc với Ox nên MP // AN
=> PN = AM (đoạn thẳng song song bị chắn bởi hai đƣờng thẳng song song) (2)
Từ (1),(2) => OP = AM.
Biện luận:
Góc xOy nhọn nên tia phân giác Ot cắt đường thẳng kẻ từ A vuông góc với Ox tại một điểm N duy nhất.Do đó bài toán có một nghiệm hình như hình vẽ.
Bài 6: Cho tam giác ABC vuông cân, cạnh huyền BC = 2a không đổi .Gọi H là trung điểm của BC .
1. Hãy dựng điểm M trên đoạn AH sao cho khoảng cách từ M đến BC bằng tổng khoảng cách đến AB và AC .
2. Tính theo a độ dài của HM tương ứng .
Phân tích bài toán :
Giả sử đã dựng được M thuộc AH mà khoảng cách từ M đến BC bằng tổng khoảng cách từ M đến AB và AC.
Ta có $N \in AP => MH = MK + ML =MN$.
=> $ \triangle MNH$ cân tại M .
=> $ \widehat{MNH}= \widehat{MHN} = \widehat{MHN} = \widehat{PHN}$ .
Cách dựng hình :
Dựng điểm P là đối xứng của điểm H qua AB.
Dựng phân giác HN của $\triangle AHB$.
Dựng NM // PH ,$ M \in AH$ thì ta có M là điểm cần dựng .
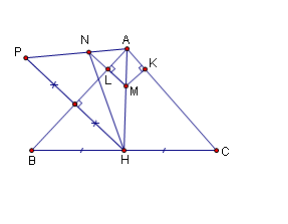
Chứng minh :
Vì : $\triangle MHN$ cân tại M => MH = MN = MK+ ML .
=> Ta dựng được hình như trên .
Biện luận:
Từ những giả thiết đề bài , ta luôn dựng được hình .
=> Bài toán có một nghiệm hình .
2.
Đặt MH = x. TA có : AH = AM + MH .
=> MA = a – x
Vì MH = 2MK <=> $ x = 2(a-x)\frac{\sqrt{2}}{2} <=> x= \frac{a\sqrt{2}}{1+\sqrt{2}}<=> x=a(2-\sqrt{2})$
Vậy $MH =a(2-\sqrt{2})$ .
