Giải chi tiết Giải SGK Toán 12 Bài 3 (Cánh diều): Biểu thức toạ độ của các phép toán vectơ – SÁCH GIÁO KHOA TOÁN 12 CÁNH DIỀU – 2024
================
Giải bài tập Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ
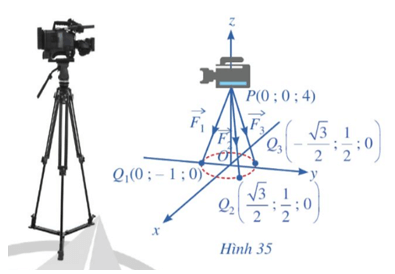
Câu hỏi khởi động trang 74 Toán 12 Tập 1: Một chiếc máy quay phim ở đài truyền hình được đặt trên một giá đỡ ba chân với điểm đặt P(0; 0; 4) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là Q1(0; – 1; 0), Q2 , Q3 (Hình 35). Biết rằng trọng lượng của máy quay là 360 N.

Làm thế nào để tìm được tọa độ của các lực tác dụng lên giá đỡ?
Lời giải:
Sau bài học này, ta giải quyết được bài toán trên như sau:
Theo giả thiết, ta có các điểm P(0; 0; 4), Q1(0; – 1; 0), Q2 , Q3 .
Suy ra 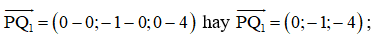
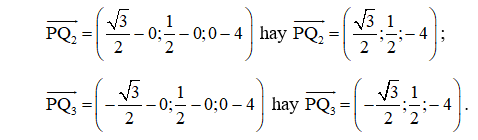
Suy ra 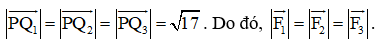
Vì vậy, tồn tại hằng số c ≠ 0 sao cho:
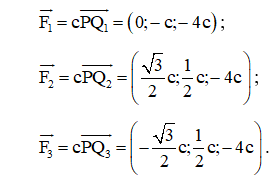
Suy ra .
Mặt khác, ta có: , trong đó là trọng lực tác dụng lên máy quay. Suy ra – 12c = – 360, tức là c = 30.
Vậy 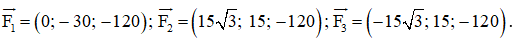
Hoạt động 1 trang 74 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz (Hình 36), cho hai vectơ và .
a) Biểu diễn các vectơ theo ba vectơ .
b) Biểu diễn các vectơ (m ∈ ℝ) theo ba vectơ .
c) Tìm tọa độ các vectơ (m ∈ ℝ).
Lời giải:
a) Ta có nên .
Ta có nên .
b)
(m ∈ ℝ).
c) Ta có .
Do đó, tọa độ của vectơ là (x1 + x2; y1 + y2; z1 + z2).
Ta có .
Do đó, tọa độ của vectơ là (x1 – x2; y1 – y2; z1 – z2).
Ta có .
Do đó, tọa độ của vectơ là (mx1; my1; mz1).
Luyện tập 1 trang 75 Toán 12 Tập 1: a) Cho . Tìm tọa độ của vectơ .
b) Cho ba điểm A(– 1; – 3; – 2), B(2; 3; 4), C(3; 5; 6). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Lời giải:
a) Ta có .
Do đó, = (– 2 + 0; 0 + 12; 1 + (– 4)) = (– 2; 12; – 3).
Suy ra = (– 2 – (– 8); 12 – 12; – 3 – 8).
Vậy = (6; 0; – 11).
b) Ta có: = (2 – (– 1); 3 – (– 3); 4 – (– 2)) = (3; 6; 6),
= (3 – (– 1); 5 – (– 3); 6 – (– 2)) = (4; 8; 8).
Ta có 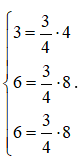 Từ đó suy ra .
Từ đó suy ra .
Do đó, hai vectơ và cùng phương.
Suy ra hai đường thẳng AB và AC song song hoặc trùng nhau, mà AB ∩ AC = A.
Vậy hai đường thẳng AB và AC trùng nhau hay ba điểm A, B, C thẳng hàng.
Hoạt động 2 trang 75 Toán 12 Tập 1: a) Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(xA; yA; zA) và B(xB; yB; zB). Gọi M(xM; yM; zM) là trung điểm của đoạn thẳng AB.
– Biểu diễn vectơ theo hai vectơ và .
– Tính tọa độ của điểm M theo tọa độ của các điểm A(xA; yA; zA) và B(xB; yB; zB).
b) Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có trọng tâm G.
– Biểu diễn vectơ theo hai vectơ , , .
– Tính tọa độ của điểm G theo tọa độ của các điểm A(xA; yA; zA), B(xB; yB; zB), C(xC; yC; zC).
Lời giải:
a)
– Vì M là trung điểm của AB nên với điểm O ta có: .
– Ta có A(xA; yA; zA) và B(xB; yB; zB) nên = (xA; yA; zA) và = (xB; yB; zB).
Khi đó, = (xA + xB; yA + yB; zA + zB).
Suy ra 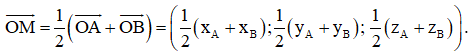
Do đó, 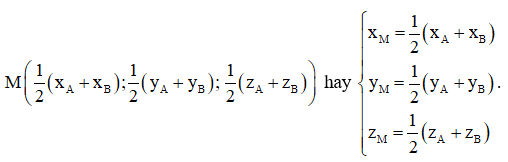
b)
– Vì G là trọng tâm của tam giác ABC nên với điểm O ta có:
.
– Ta có A(xA; yA; zA), B(xB; yB; zB), C(xC; yC; zC).
Suy ra = (xA; yA; zA), = (xB; yB; zB), = (xC; yC; zC).
Khi đó, = (xA + xB + xC; yA + yB + yC; zA + zB + zC).
Suy ra
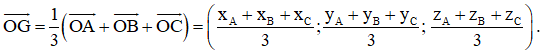
Do đó,
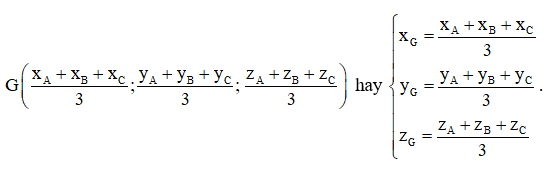
Luyện tập 2 trang 76 Toán 12 Tập 1: Cho ba điểm A(0; – 1; 1), B(1; 0; 5), G(1; 2; 0).
a) Chứng minh rằng ba điểm A, B, G không thẳng hàng.
b) Tìm tọa độ điểm C sao cho G là trọng tâm của tam giác ABC.
Lời giải:
a) Ta có .
Suy ra ới mọi k ∈ ℝ nên hai vectơ à không cùng phương.
Vậy ba điểm A, B, G không thẳng hàng.
b) Gọi tọa độ điểm C là (xC; yC; zC).
Vì G là trọng tâm của tam giác ABC nên ta có 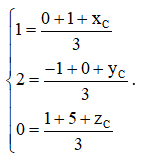
Suy ra xC = 3 – 1 = 2, yC = 6 + 1 = 7, zC = 0 – 6 = – 6.
Vậy C(2; 7; – 6).
Hoạt động 3 trang 76 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho các vectơ , .
Hãy biểu diễn các vectơ theo ba vectơ đơn vị và tính tích vô hướng .
Lời giải:
Ta có , .
Do đó, , .
Ta có
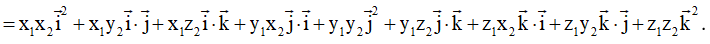
Mà và (do là ba vectơ đơn vị đôi một vuông góc với nhau).
Do đó, .
Luyện tập 3 trang 77 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(2; – 1; 1), B(1; – 1; 2) và C(3; 0; 2). Chứng minh rằng tam giác ABC vuông tại A.
Lời giải:
Ta có .
Nhận thấy (– 1) ∙ 1 + 0 ∙ 1 + 1 ∙ 1 = – 1 + 1 = 0, do đó .
Suy ra hai vectơ và vuông góc với nhau hay hai đường thẳng AB và AC vuông góc với nhau.
Vậy tam giác ABC vuông tại A.
Hoạt động 4 trang 79 Toán 12 Tập 1: a) Cho hình lập phương ABCD.A’B’C’D’ có A(0; 0; 0), B(1; 0; 0), D(0; 1; 0), C'(1; 1; 1). Hãy chỉ ra tọa độ của một vectơ vuông góc với cả hai vectơ và .
b) Cho hai vectơ và không cùng phương.
Xét vectơ .
– Tính .
– Vectơ có vuông góc với cả hai vectơ và hay không?
Lời giải:
a)
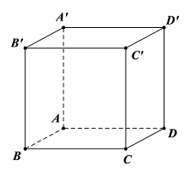
Ta có .
Gọi tọa độ điểm C là (xC; yC; zC), ta có (xC; yC – 1; zC).
Vì là ABCD.A’B’C’D’ hình lập phương nên .
Suy ra 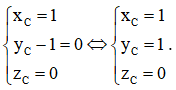 Do đó, C(1; 1; 0).
Do đó, C(1; 1; 0).
Ta có .
Ta thấy 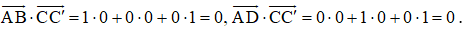
Vậy vectơ vuông góc với cả hai vectơ và .
b)
– Ta có:
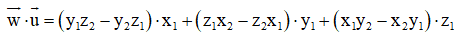
= y1z2x1 – y2z1x1 + z1x2y1 – z2x1y1 + x1y2z1 – x2y1z1
= (y1z2x1 – z2x1y1) + (x1y2z1 – y2z1x1) + (z1x2y1 – x2y1z1) = 0;
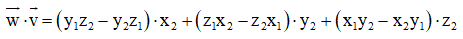
= y1z2x2 – y2z1x2 + z1x2y2 – z2x1y2 + x1y2z2 – x2y1z2
= (y1z2x2 – x2y1z2) + (x1y2z2 – z2z1y2) + (z1x2y2 – y2z1x2) = 0.
– Vì nên vectơ vuông góc với cả hai vectơ và .
Luyện tập 4 trang 80 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho hai vectơ và . Hãy chỉ ra tọa độ của một vectơ khác vuông góc với cả hai vectơ và .
Lời giải:
Ta có 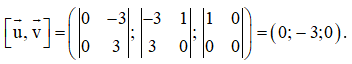
Chọn = (0; – 3; 0).
Vậy vectơ vuông góc với cả hai vectơ và .
Bài tập
Bài 1 trang 80 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho và . Tọa độ của vectơ là:
A. (1; – 2; 1).
B. (5; 4; – 3).
C. (– 1; 2; – 1).
D. (– 1; 2; – 3).
Lời giải:
Đáp án đúng là: C
Ta có = (2 – 3; 3 – 1; – 2 – (– 1)). Do đó = (– 1; 2; – 1).
Bài 2 trang 80 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho và . Góc giữa hai vectơ và bằng:
A. 60°.
B. 120°.
C. 150°.
D. 30°.
Lời giải:
Đáp án đúng là: A
Ta có 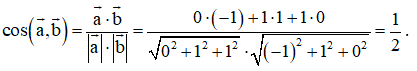
Suy ra .
Bài 3 trang 80 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho , .
a) Tìm tọa độ của vectơ .
b) Tìm tọa độ của vectơ sao cho .
Lời giải:
a) Ta có , do đó = (– 2 + 3; 4 + 1; 6 + (– 2)) = (1; 5; 4).
Lại có , do đó = (1 – 12; 5 – 6; 4 – (– 9)).
Vậy = (– 11; – 1; 13).
b) Ta có , suy ra .
= (– 1 + 4; 2 + 2; 3 + (– 3)) = (3; 4; 0).
Mà , do đó = (3 – 6; 4 – 2; 0 – (– 4)).
Vậy = (– 3; 2; 4).
Bài 4 trang 80 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho . Hãy chỉ ra tọa độ của một vectơ khác vuông góc với cả hai vectơ và .
Lời giải:
Ta có 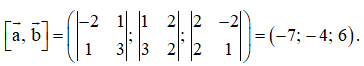
Chọn , ta có vectơ vectơ vuông góc với cả hai vectơ và .
Bài 5 trang 81 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho . Tính côsin của góc .
Lời giải:
Ta có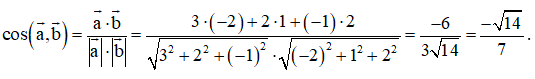
Bài 6 trang 81 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho A(– 2; 3; 0), B(4; 0; 5), C(0; 2; – 3).
a) Chứng minh rằng ba điểm A, B, C không thẳng hàng.
b) Tính chu vi tam giác ABC.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tính .
Lời giải:
a) Ta có , .
Suy ra với mọi k ∈ ℝ, do đó hai vectơ và không cùng phương.
Vậy ba điểm A, B, C không thẳng hàng.
b) Ta có 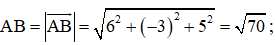
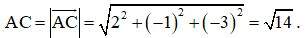
Ta có .
Suy ra 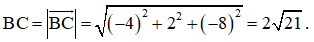
Chu vi tam giác ABC là C = AB + AC + BC = .
c) Gọi tọa độ trọng tâm G của tam giác ABC là (xG; yG; zG).
Ta có ; .
Vậy .
d) Ta có 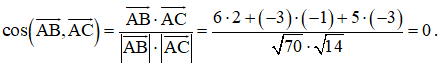
Do đó hai vectơ và vuông góc với nhau hay hai đường thẳng AB và AC vuông góc với nhau nên . Vậy = 0.
Bài 7 trang 81 Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’, biết A(1; 0; 1), B(2; 1; 2), D(1; – 1; 1), C'(4; 5; – 5). Hãy chỉ ra tọa độ của một vectơ khác vuông góc với cả hai vectơ trong mỗi trường hợp sau:
a) và ;
b) và .
Lời giải:
a) Ta có , ,
Vì ABCD.A’B’C’D’ là hình hộp nên ABCD là hình bình hành, do đó
.
Ta có .
Vì ABCD.A’B’C’D’ là hình hộp nên .
Ta có 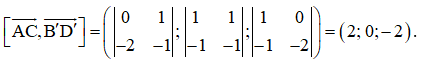
Chọn , vectơ vuông góc với cả hai vectơ và .
b) Ta có , .
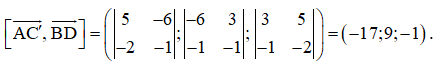
Chọn , vectơ vuông góc với cả hai vectơ và .
Bài 8 trang 81 Toán 12 Tập 1: Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên trần nhà lần lượt buộc vào ba điểm A, B, C trên đèn tròn sao cho tam giác ABC đều (Hình 38). Độ dài của ba đoạn dây OA, OB, OC đều bằng L. Trọng lượng của chiếc đèn là 24 N và bán kính của chiếc đèn là 18 in (1 inch = 2,54 cm). Gọi F là độ lớn của các lực căng trên mỗi sợi dây. Khi đó, F = F(L) là một hàm số với biến số là L.
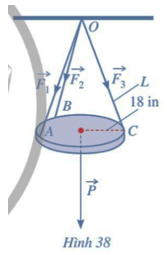
a) Xác định công thức tính hàm số F = F(L).
b) Khảo sát và vẽ đồ thị hàm số F = F(L).
c) Tìm chiều dài tối thiểu của mỗi sợi dây, biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là 10 N.
Lời giải:
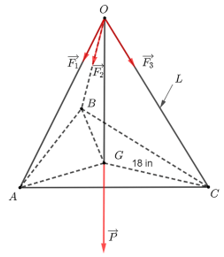
a) Ta có 18 in = 45,72 cm = 0,4572 m.
Gọi G là trọng tâm tam giác ABC.
Vì tam giác ABC đều nên G là tâm đường tròn ngoại tiếp tam giác ABC.
Do đó, GA = GB = GC = 0,4572 m.
Theo bài ra ta có OA = OB = OC = L nên OG ⊥ (ABC) và 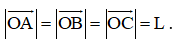
Do đó, 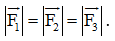
Vì vậy, tồn tại hằng số c ≠ 0 sao cho: .
Suy ra .
Theo quy tắc ba điểm ta có
(do G là trọng tâm tam giác ABC nên ).
Do đó, .
Mặt khác ta lại có , với là trọng lực tác dụng lên chiếc đèn.
Mà trọng lượng tác dụng lên chiếc đèn là 24 N nên 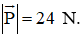
Từ đó suy ra 
Tam giác OAG vuông tại G (do OG ⊥ (ABC)) nên ta suy ra
(m) với L > 0,4572.
Do đó, 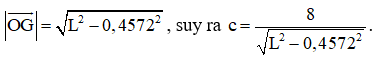
Khi đó, 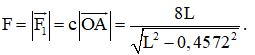
Vậy với L > 0,4572.
b) Xét hàm số với L ∈ (0,4572; + ∞).
+ Tập xác định: D = (0,4572; + ∞).
+ Sự biến thiên
– Giới hạn tại vô cực giới hạn vô cực và các đường tiệm cận:
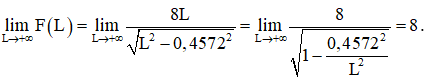 Do đó, đường thẳng F = 8 là tiệm cận ngang của đồ thị hàm số.
Do đó, đường thẳng F = 8 là tiệm cận ngang của đồ thị hàm số.
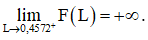 Do đó, đường thẳng L = 0,4572 là tiệm cận đứng của đồ thị hàm số.
Do đó, đường thẳng L = 0,4572 là tiệm cận đứng của đồ thị hàm số.
+ Đạo hàm < 0 với mọi L ∈ (0,4572; + ∞).
+ Bảng biến thiên:
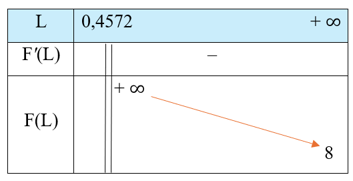
Hàm số nghịch biến trên khoảng (0,4572; + ∞).
Hàm số không có cực trị.
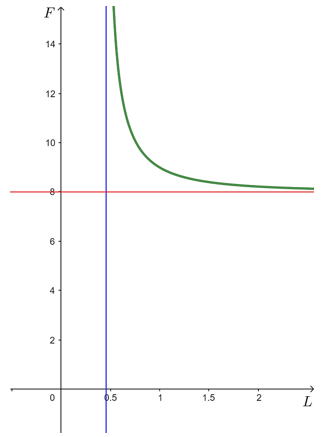
+ Đồ thị hàm số được vẽ như hình dưới đây:
c) Ta có lực căng tối đa của mỗi sợi dây là 10 N.
Với F(L) = 10, ta có . Từ đó suy ra
⇔ 25L2 – 5,255796 = 16L2
⇒ L = 0,762 ∈ (0,4572; + ∞).
Vậy chiều dài tối thiểu của mỗi sợi dây là L = 0,762 m = 76,2 cm = 30 in.
=============
THUỘC: Giải bài tập Toán 12 – SGK CÁNH DIỀU
