Giải chi tiết Giải SGK Toán 12 (CTST) Bài 3: Biểu thức toạ độ của các phép toán vectơ – SÁCH GIÁO KHOA TOÁN 12 CHÂN TRỜI – 2024
================
Sách Chân trời sáng tạo – Giải bài tập Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ
Hoạt động khởi động trang 58 Toán 12 Tập 1: Trong không gian Oxyz, có thể thực hiện các phép toán vectơ dựa trên tọa độ của chúng tương tự như đã làm trong mặt phẳng Oxy không?

Lời giải:
Trong không gian Oxyz, ta có thể thực hiện các phép toán vectơ dựa trên tọa độ của chúng tương tự như đã làm trên mặt phẳng tọa độ.
1. Biểu thức tọa độ của tổng, hiệu hai vectơ và tích của một số với một vectơ
Hoạt động khám phá 1 trang 58 Toán 12 Tập 1: Trong không gian Oxyz, cho hai vectơ , với số thực m.
a) Biểu diễn từng vectơ và theo ba vectơ .
b) Biểu diễn các vectơ theo ba vectơ , từ đó suy ra tọa độ của các vectơ .
Lời giải:
a) ; .
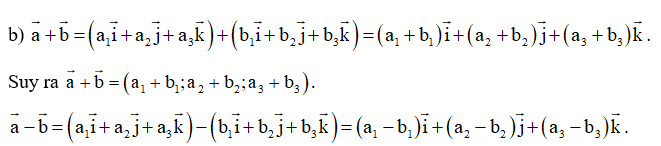
Suy ra .
Suy ra
Thực hành 1 trang 59 Toán 12 Tập 1: Cho ba vectơ .
a) Tìm tọa độ của vectơ .
b) Tìm tọa độ của vectơ .
c) Chứng minh cùng phương với vectơ .
Lời giải:
a) .
Khi đó .
b) .
Khi đó = (0; −27; 3).
c) Có .
Do đó cùng phương với vectơ .
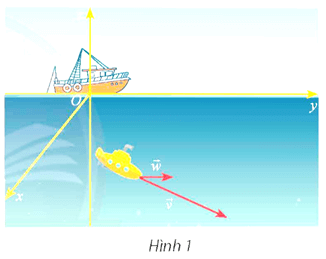
Vận dụng 1 trang 59 Toán 12 Tập 1: Một thiết bị thăm dò đáy biển đang lặn với vận tốc (Hình 1). Cho biết vận tốc của dòng hải lưu của vùng biển là .
a) Tìm tọa độ của vectơ tổng hai vận tốc và .
b) Giả sử thiết bị thăm dò lặn với vận tốc , hãy nêu nhận xét về vectơ vận tốc của nó so với vectơ vận tốc của dòng hải lưu.
Lời giải:
a) .
b) Vì .
Do đó hai vectơ này cùng phương, cùng hướng với nhau.
2. Biểu thức tọa độ của tích vô hướng
Hoạt động khám phá 2 trang 59 Toán 12 Tập 1: Cho hai vectơ và .
a) Biểu diễn từng vectơ và theo ba vectơ .
b) Tính các tích vô hướng .
c) Tính tích vô hướng theo tọa độ của hai vectơ và .
Lời giải:
a) và .
b)
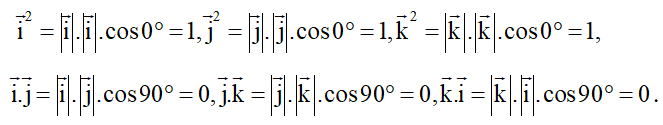
c)
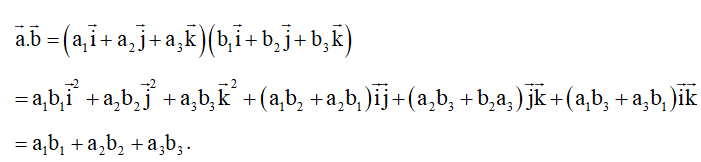
Thực hành 2 trang 60 Toán 12 Tập 1: Cho ba vectơ , , .
a) Tính .
b) Tính .
c) Cho . Vectơ có vuông góc với không?
Lời giải:
a) .
b)
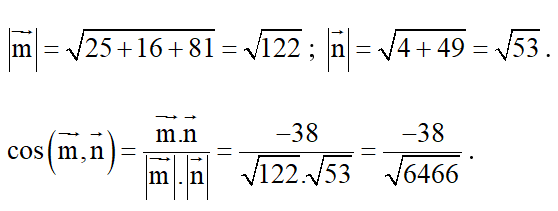
c) Có . Do đó .
Vận dụng 2 trang 60 Toán 12 Tập 1: Một thiết bị thăm dò đáy biển (Hình 2) được đẩy bởi một lực (đơn vị: N) giúp thiết bị thực hiện độ dời (đơn vị: m). Tính công sinh bởi lực .
Lời giải:
Công sinh bởi lực được tính theo công thức
J.
3. Vận dụng
Hoạt động khám phá 3 trang 60 Toán 12 Tập 1: Cho hai điểm . Từ biểu thức , tìm tọa độ của vectơ theo tọa độ hai điểm A, B.
Lời giải:
Ta có .
Do đó .
Thực hành 3 trang 61 Toán 12 Tập 1: Cho ba điểm M(7; −2; 0), N(−9; 0; 4), P(0; −6; 5).
a) Tìm tọa độ của các vectơ .
b) Tính các độ dài MN, NP, MP.
Lời giải:
a) ;
;
.
b) .
.
.
Hoạt động khám phá 4 trang 61 Toán 12 Tập 1: Cho tam giác ABC có A(xA; yA; zA), B(xB; yB; zB), C(xC; yC; zC). Gọi M(xM; yM; zM) là trung điểm của đoạn thẳng AB và G(xG; yG; zG) là trọng tâm của tam giác ABC. Sử dụng các hệ thức vectơ , tìm tọa độ của các điểm M và G.
Ta có .
Có 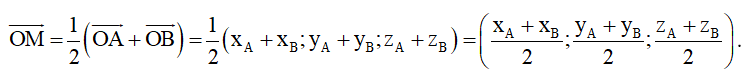
Do đó .
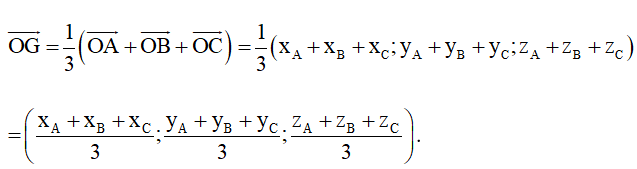
Do đó .
Thực hành 4 trang 62 Toán 12 Tập 1: Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(−3;−1; 0). Tìm tọa độ:
a) Các điểm M’, N’, P’ lần lượt là trung điểm của các cạnh NP, MP, MN;
b) Trọng tâm G của tam giác M’N’P’.
Lời giải:
a) Tọa độ trung điểm M’ của cạnh NP là
hay .
Tọa độ trung điểm N’ của cạnh MP là
hay .
Tọa độ trung điểm P’ của cạnh MN là
hay .
b) Tọa độ trọng tâm G là:
hay .
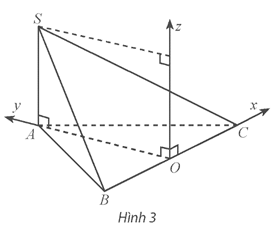
Vận dụng 3 trang 62 Toán 12 Tập 1: Cho hình chóp S.ABC có SA (ABC), SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ tọa độ như Hình 3, hãy tìm tọa độ:
a) Các điểm A, S, B, C.
b) Trung điểm M của SB và trung điểm N của SC.
c) Trọng tâm G của tam giác SBC.
Lời giải:
a)
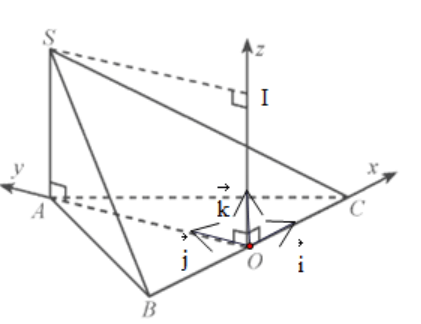
Vì ABC là tam giác đều cạnh a, O là trung điểm của BC nên AO là đường cao.
Suy ra và OB = OC = .
Vì và cùng hướng và nên . Suy ra .
Vì và ngược hướng và nên . Suy ra .
Vì và cùng hướng và nên . Suy ra
Gọi I là hình chiếu của S trên Oz.
Ta có OI = SA.
Vì OI và cùng hướng và OI = a nên .
Theo quy tắc hình bình hành có: .
Do đó .
b) Tọa độ trung điểm M của SB là
hay .
Tọa độ trung điểm N của SC là
hay .
c) Tọa độ trọng tâm G của tam giác SBC là:
hay .
Thực hành 5 trang 63 Toán 12 Tập 1: Cho tam giác MNP có M(0; 1; 2), N(5; 9; 3), P(7; 8; 2).
a) Tìm tọa độ điểm K là chân đường cao kẻ từ M của tam giác MNP.
b) Tìm độ dài cạnh MN và MP.
c) Tính góc M.
Lời giải:
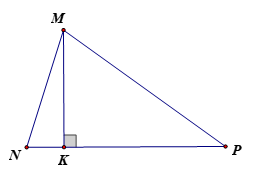
a) Ta có .
Vì K là chân đường vuông góc kẻ từ M xuống NP nên K NP và MK NP.
Gọi K(x; y; z), ta có .
Vì và cùng phương nên tồn tại t ℝ sao cho .
Do đó . Suy ra K(7 – 2t; 8 + t; 2 + t).
Khi đó .
Vì MK NP nên
Vậy .
b) Ta có ; .
; .
c) Ta có
Vận dụng 4 trang 64 Toán 12 Tập 1: Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một đội gồm ba drone giao hàng A, B, C đang có tọa độ là A(1; 1; 1), B(5; 7; 9), C(9; 11; 4). Tính:
a) Các khoảng cách giữa mỗi cặp drone giao hàng.
b) Góc .
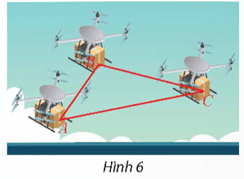
Lời giải:
a) Ta có ; ; .
Khi đó: ;
;
.
b) Ta có .
Bài tập
Bài 1 trang 64 Toán 12 Tập 1: Tính:
a) với .
b) với .
Lời giải:
a) .
b) .
Bài 2 trang 64 Toán 12 Tập 1: Cho hai vectơ và . Tìm tọa độ của vectơ .
Lời giải:
Có ; .
Tọa độ của vectơ là hay .
Bài 3 trang 64 Toán 12 Tập 1: Cho ba điểm A(2; 1; −1), B(3; 2; 0) và C(2; −1; 3).
a) Chứng minh A, B, C là ba đỉnh của một tam giác. Tính chu vi tam giác ABC.
b) Tìm tọa độ trung điểm của các cạnh của tam giác ABC.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
Lời giải:
a) Ta có .
Vì và không cùng phương nên A, B, C không thẳng hàng.
Do đó A, B, C là ba đỉnh của một tam giác.
Ta có chu vi tam giác ABC là:
AB + AC + BC
=
b) Gọi M, N, P lần lượt là trung điểm của cạnh AB, BC, CA.
Tọa độ điểm M là
hay .
Tọa độ điểm N là
hay .
Tọa độ điểm P là
hay .
c) Tọa độ trọng tâm G của tam giác ABC là
hay .
Bài 4 trang 64 Toán 12 Tập 1: Cho điểm M(1; 2; 3). Hãy tìm tọa độ của các điểm:
a) M1, M2, M3 lần lượt là hình chiếu vuông góc của M trên các mặt phẳng (Oxy), (Oyz), (Oxz).
b) Gọi M’, M”, M”‘ lần lượt là các điểm thỏa mãn:
• O là trung điểm của MM’;
• MM” vuông góc với mặt phẳng (Oxy) tại điểm H sao cho H là trung điểm của MM”.
• MM”‘ vuông góc và cắt trục Oy tại điểm K sao cho K là trung điểm của MM”‘.
Lời giải:
a) Ta có M1(1; 2; 0), M2(0; 2; 3), M3(1; 0; 3).
b) +) Vì O là trung điểm của MM’ nên
Vậy M'(−1; −2; −3).
+) Vì H (Oxy) nên H(x; y; 0).
Ta có .
Vì MH (Oxy)
Do đó H(1; 2; 0).
Vì H là trung điểm của MM” nên
Vậy M”(1; 2; −3).
+) Vì K Oy nên K(0; y; 0)
Vì nên . Do đó K(0; 2; 0).
Vì K là trung điểm của MM”‘ nên
Vậy M”'(−1; 2; −3).
Bài 5 trang 64 Toán 12 Tập 1: Cho ba điểm A(3; 3; 3), B(1; 1; 2) và C(5; 3; 1).
a) Tìm điểm M trên trục Oy cách đều hai điểm B, C.
b) Tìm điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C.
Lời giải:
a) Vì M Oy nên M(0; y; 0).
Vì M cách đều hai điểm B, C nên MB = MC hay MB2 = MC2
Vậy .
b) Vì N (Oxy) nên N(x; y; 0).
Vì N cách đều ba điểm A, B, C nên NA = NB = NC hay NA2 = NB2 = NC2
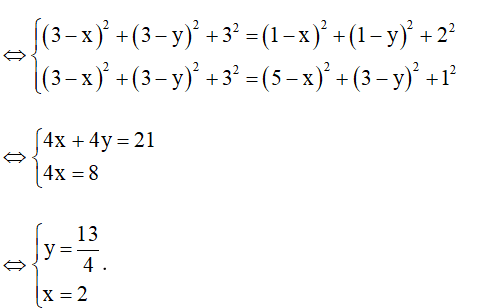
Vậy .
Bài 6 trang 64 Toán 12 Tập 1: Cho các điểm A(−1; −1; 0), B(0; 3; −1), C(−1; 14; 0), D(−3; 6; 2). Chứng minh rằng ABCD là hình thang.
Ta có , , .
Vì nên và cùng phương.
Mặt khác và không cùng phương nên CD // AB.
Do đó ABCD là hình thang.
Bài 7 trang 64 Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’ có A(1; 0; 1), B(2; 1; 2), D(1; −1; 1), C'(4; 5; −5). Tìm tọa độ các đỉnh còn lại của hình hộp.
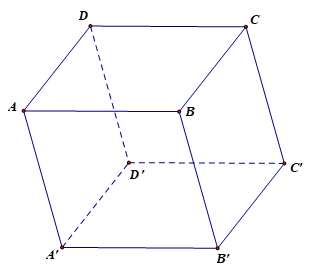
Do ABCD.A’B’C’D’ là hình hộp nên các mặt là hình bình hành.
Ta có .
Vậy C(2; 0; 2).
Ta có .
Vậy D'(3; 4; −6).
Ta có .
Vậy A'(3; 5; −6).
Ta có .
Vậy B'(4; 6; −5).
Bài 8 trang 64 Toán 12 Tập 1: Tính công sinh bởi lực (đơn vị: N) tạo bởi một drone giao hàng (Hình 7) khi thực hiện một độ dịch chuyển (đơn vị: m).
Lời giải:

Lời giải:
Công sinh bởi lực là = 20.150 + 30.200 + (-10).100 = 8000 J.
=============
THUỘC: Giải bài tập Toán 12 – SGK CHÂN TRỜI
