Giải Bài 8. Sự thống nhất giữa ba đường conic – Chuyên đề Toán 10 (Kết nối)

Giải Bài 8. Sự thống nhất giữa ba đường conic – Chuyên đề Toán 10 (Kết nối)
———–

Giải mục 2 trang 59 Chuyên đề học tập Toán 10

Lựa chọn câu để xem lời giải nhanh hơn

Luyện tập 1

Lập phương trình đường conic biết tâm sai bằng \(\frac{2}{3}\), một tiêu điểm \(F( – 2;0)\) và đường chuẩn tương ứng \(\Delta: x + \frac{9}{2} = 0\)

Phương pháp giải:

Cho đường conic có tâm sai \(e > 0\), đường chuẩn \(\Delta \) không đi qua tiêu điểm F.

Khi đó: \(\frac{{MF}}{{d(M,\Delta )}} = e\) với M bất kì thuộc conic đó.

Lời giải chi tiết:

Điểm \(M(x;y)\) thuộc đường conic khi và chỉ khi

\(\begin{array}{l}\frac{{MF}}{{d(M,\Delta )}} = \frac{2}{3} \Leftrightarrow 3.\sqrt {{{(x + 2)}^2} + {y^2}}  = 2\left| {x + \frac{9}{2}} \right|\\ \Leftrightarrow 9\left[ {{{(x + 2)}^2} + {y^2}} \right] = 4.{\left( {x + \frac{9}{2}} \right)^2}\\ \Leftrightarrow 5{x^2} + 9{y^2} = 45\\ \Leftrightarrow \frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1\end{array}\)

Vậy đường conic có phương trình là \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1\)

Vận dụng 2

Hãy cho biết quỹ đạo của từng vật thể trong bảng sau đây là parabol, elip hay hypebol.

Tên	Tâm sai của quỹ đạo	Ngày phát hiện
Sao chổi Halley	0,967	TCN
Sao chổi Hale-Bopp	0,995	23/07/1995
Sao chổi Hyakutake	0,999	31/01/1996
Sao chổi C/1980E1	1,058	11/02/1980
Oumuamua	1,201	19/10/2017

(Theo nssdc.gsfc.nasa.gov và astronomy.com)

Phương pháp giải:

Đường conic có tâm sai e:

+ \(0 < e < 1\) thì conic là đường elip

+ \(e = 1\) thì conic là đường parabol

+ \(e > 1\) thì conic là đường hypebol

Lời giải chi tiết:

Tên	Tâm sai của quỹ đạo	So sánh với 0 và 1	Kết luận
Sao chổi Halley	0,967	0 < 0,967 < 1	Elip
Sao chổi Hale-Bopp	0,995	0 < 0,995 < 1	Elip
Sao chổi Hyakutake	0,999	0 < 0,999 < 1	Elip
Sao chổi C/1980E1	1,058	1,058 > 1	hypebol
Oumuamua	1,201	1,201 > 1	hypebol

Giải bài 3.17 trang 60 Chuyên đề học tập Toán 10

Đề bài

Viết phương trình các đường chuẩn của các đường conic sau:

a) \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)

b) \(\frac{{{x^2}}}{9} – \frac{{{y^2}}}{4} = 1\)

c) \({y^2} = 8x\)

Elip có PTCT  \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có đường chuẩn \({\Delta _1}: x =  – \frac{a}{e}\) và \({\Delta _2}: x = \frac{a}{e}\)

(\(e = \frac{c}{a};c = \sqrt {{a^2} – {b^2}} \))

Hypebol có PTCT  \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) có đường chuẩn \({\Delta _1}: x =  – \frac{a}{e}\) và \({\Delta _2}: x = \frac{a}{e}\)

(\(e = \frac{c}{a};c = \sqrt {{a^2} + {b^2}} \))

Parabol có PTCT  \({y^2} = 2px\) có đường chuẩn \(\Delta : x =  – \frac{p}{2}\)

Lời giải chi tiết

a) Elip có PTCT  \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)

\( \Rightarrow a = 5;b = 4 \Rightarrow c = 3;e = \frac{3}{5} \Rightarrow \frac{a}{e} = \frac{{25}}{3}.\)

(E) có đường chuẩn \({\Delta _1}: x =  – \frac{{25}}{3}\) và \({\Delta _2}: x = \frac{{25}}{3}\)

b) Hypebol có PTCT  \(\frac{{{x^2}}}{9} – \frac{{{y^2}}}{4} = 1\)

\( \Rightarrow a = 3;b = 2 \Rightarrow c = \sqrt {13} ;e = \frac{{\sqrt {13} }}{3} \Rightarrow \frac{a}{e} = \frac{9}{{\sqrt {13} }} = \frac{{9\sqrt {13} }}{{13}}.\)

(H) có đường chuẩn \({\Delta _1}: x =  – \frac{{9\sqrt {13} }}{{13}}\) và \({\Delta _2}: x = \frac{{9\sqrt {13} }}{{13}}\)

c) Parabol có PTCT  \({y^2} = 8x\)

\( \Rightarrow 2p = 8 \Leftrightarrow p = 4\)

 (P) có đường chuẩn \(\Delta : x =  – \frac{p}{2} =  – 2\)

 

Giải bài 3.18 trang 60 Chuyên đề học tập Toán 10

Đề bài

Cho hai elip \(({E_1}):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) và \(({E_2}):\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)

a) Tìm mối quan hệ giữa hai tâm sai của các elip đó

b) Chứng minh rằng với mỗi điểm M thuộc elip \(({E_2})\) thì trung điểm N của đoạn thẳng OM thuộc elip \(({E_1}).\)

Elip có PTCT  \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có tâm sai \(e = \frac{c}{a}\), trong đó \(c = \sqrt {{a^2} – {b^2}} .\)

Lời giải chi tiết

a) \(({E_1}):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) có \(a = 5,b = 4 \Rightarrow c = 3\)

Vậy tâm sai \({e_1} = \frac{3}{5}\)

\(({E_2}):\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\) có \(a = 10,b = 8 \Rightarrow c = 6\)

Vậy tâm sai \({e_2} = \frac{6}{{10}} = \frac{3}{5} = {e_1}\)

b) Giả sử \(M({x_0};{y_0})\) thuộc \(({E_2}).\)

\( \Rightarrow \) Trung điểm N của OM là: \(N(\frac{{{x_0}}}{2};\frac{{{y_0}}}{2})\)

Ta có: \(\frac{{{x_0}^2}}{{100}} + \frac{{{y_0}^2}}{{64}} = 1 \Leftrightarrow \frac{{\frac{{{x_0}^2}}{4}}}{{25}} + \frac{{\frac{{{y_0}^2}}{4}}}{{16}} = 1 \Leftrightarrow \frac{{{{\left( {\frac{{{x_0}}}{2}} \right)}^2}}}{{25}} + \frac{{{{\left( {\frac{{{y_0}}}{2}} \right)}^2}}}{{16}} = 1\)

\( \Rightarrow \) N thuộc \(({E_1}).\)

 

Giải bài 3.19 trang 60 Chuyên đề học tập Toán 10

Đề bài

Viết phương trình của đường conic có tâm sai bằng 1, tiêu điểm F(2; 0) và đường chuẩn là \(\Delta : x + 2 = 0\)

Bước 1: Xác định loại đường conic dựa vào tâm sai e:

+ \(0 < e < 1\) thì conic là đường elip

+ \(e = 1\) thì conic là đường parabol

+ \(e > 1\) thì conic là đường hypebol

Bước 2: Tìm tập hợp các điểm M sao cho \(\frac{{MF}}{{d(M,\Delta )}} = e\)

Từ đó kết luận phương trình đường conic.

Lời giải chi tiết

Đường conic có tâm sai bằng 1 thì là parabol.

Điểm \(M(x,y)\) thuộc đường conic khi và chỉ khi

\(\begin{array}{l}\frac{{MF}}{{d(M,\Delta )}} = 1 \Leftrightarrow \frac{{\sqrt {{{\left( {x – 2} \right)}^2} + {y^2}} }}{{\left| {x + 2} \right|}} = 1\\ \Leftrightarrow \sqrt {{{\left( {x – 2} \right)}^2} + {y^2}}  = \left| {x + 2} \right|\\ \Leftrightarrow {\left( {x – 2} \right)^2} + {y^2} = {\left( {x + 2} \right)^2}\\ \Leftrightarrow {y^2} = 8x\end{array}\)

Giải bài 3.20 trang 60 Chuyên đề học tập Toán 10

Đề bài

Quỹ đạo chuyển động của sao chổi Halley là một elip, nhận tâm Mặt Trời là một tiêu điểm, có tâm sai bằng 0,967.

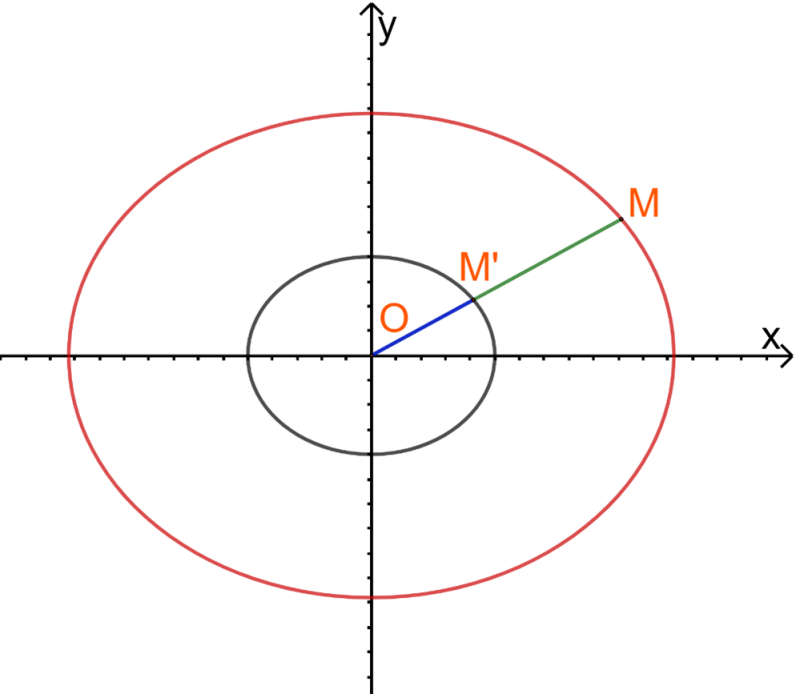
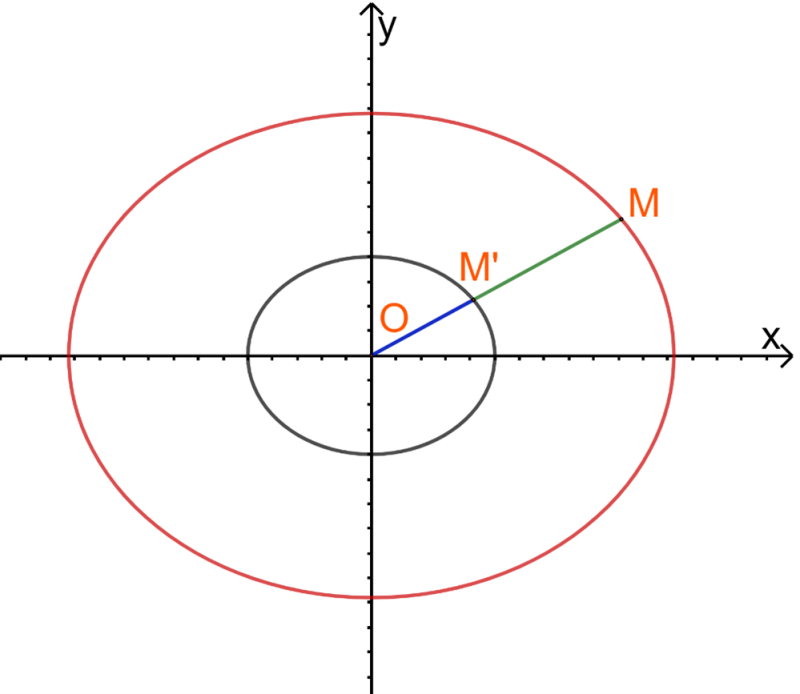
a) Giải thích vì sao ta có thể coi bất kì hình vẽ elip nào với tâm sai bằng 0,967 là hình ảnh thu nhỏ của quỹ đạo sao chổi Halley.

b) Biết khoảng cách gần nhất từ sao chổi Halley đến tâm Mặt Trời là khoảng \({88.10^6}\) km, tính khoảng cách xa nhất (theo nssdc.gsfc.nasa.gov).

a) Bước 1: Gọi (E) và (E’) là 2 elip có cùng tâm sai.

Bước 2: Lấy M bất kì thuộc (E), chỉ ra tồn tại M’ thuộc (E’) thỏa mãn:

\(\overrightarrow {OM’}  = \frac{1}{k}\overrightarrow {OM} \)

b) Với \(M({x_0};{y_0})\) bất kì thuộc (E), ta có:

\(M{F_1}\) nhỏ nhất bằng \(a – c = {88.10^6}\)

\(M{F_1}\) lớn nhất bằng \(a + c\)

Lời giải chi tiết

a) Giả sử quỹ đạo chuyển động của sao chổi Halley có phương trình chính tắc:

\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (E)

Gọi (E’) là elip bất kì với tâm sai \(e’ = e = 0,967\), có PTCT: \(\frac{{{x^2}}}{{a{‘^2}}} + \frac{{{y^2}}}{{b{‘^2}}} = 1\) (a’<a)

\(e’ = e\) hay \(\frac{{c’}}{{a’}} = \frac{c}{a} \Leftrightarrow \frac{{\sqrt {a{‘^2} – b{‘^2}} }}{{a’}} = \frac{{\sqrt {{a^2} – {b^2}} }}{a}\)

\( \Leftrightarrow \frac{{a{‘^2} – b{‘^2}}}{{a{‘^2}}} = \frac{{{a^2} – {b^2}}}{{{a^2}}} \Leftrightarrow 1 – \frac{{b{‘^2}}}{{a{‘^2}}} = 1 – \frac{{{b^2}}}{{{a^2}}} \Leftrightarrow \frac{{b’}}{{a’}} = \frac{b}{a} \Leftrightarrow \frac{b}{{b’}} = \frac{a}{{a’}} = k\) (k>1)

Lấy \(M({x_0};{y_0})\) bất kì thuộc (E) ta có:

\(\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1 \Leftrightarrow \frac{{{x_0}^2}}{{{{\left( {ka’} \right)}^2}}} + \frac{{{y_0}^2}}{{{{\left( {kb’} \right)}^2}}} = 1 \Leftrightarrow \frac{{{{\left( {\frac{{{x_0}}}{k}} \right)}^2}}}{{a{‘^2}}} + \frac{{{{\left( {\frac{{{y_0}}}{k}} \right)}^2}}}{{b{‘^2}}} = 1\)

\( \Rightarrow M'(\frac{1}{k}{x_0};\frac{1}{k}{y_0}) \in (E’)\)

Dễ thấy \(\overrightarrow {OM’}  = \frac{1}{k}\overrightarrow {OM} \) với mọi M thuộc (E)

Nói cách khác, (E’) là một elip thu nhỏ của (E).

b) Giả sử tâm Mặt Trời ở vị trí tiêu điểm \({F_1}( – c;0)\)

Với \(M({x_0};{y_0})\) bất kì thuộc (E), ta có:

\(M{F_1}\) nhỏ nhất bằng \(a – c = {88.10^6}\)

Mà \(e = \frac{c}{a} = 0,967\)

\( \Rightarrow \left\{ \begin{array}{l}a = \frac{8}{3}{.10^9} \approx 2\;666\;666\;667\\c \approx 2\;578\;666\;667\end{array} \right.\)

\( \Rightarrow \)\(M{F_1}\) lớn nhất bằng \(a + c = 5\;245\;333\;334\) (km).

Vậy khoảng cách xa nhất từ sao chổi Halley đến tâm Mặt trời là 5 245 333 334 km.