Lý thuyết Bài 2: Tập hợp và các phép toán trên tập hợp
=============
Tóm tắt lý thuyết
1.1. Các khái niệm cơ bản về tập hợp
a) Tập hợp
|
Có thể mô tả một tập hợp bằng một trong hai cách sau: Cách 1: Liệt kê các phần tử của tâp hợp; Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp. |
|---|
Chú ý: Số phần tử của tập hợp S được kí hiệu là n(S).
- a \( \in \) S phần tử a thuộc tập hợp S.
- a \( \notin \) S phần tử a không thuộc tập hợp S.
* Tập hợp không chưa phần tử nào được gọi là tập rộng, kí hiệu là \(\emptyset \)
Chẳng hạn:
– Tập hợp các nghiệm của phương trình x2 + 1 = 0 là tập rộng;
– Tập hợp những người sống trên Mặt Trời là tập rỗng.
b) Tập hợp con
| Nếu mọi phần tử của tập hợp T đều là phần tử của tập hợp S thì ta nói T là một tập hợp con (tập con) của S và viết là \(T \subset S\) (đọc là T chứ trong S hoặc T là tập hợp con của S). |
|---|
- Thay cho \(T \subset S\), ta còn viết \(S \supset T\) (đọc là S chứa T).
- Kí hiệu \(T \not\subset S\) để chỉ T không lả tập con của S.
Nhận xét:
- Từ định nghĩa trên, T là tập con của S nếu mệnh đề sau đúng: \(\forall x,x \in T \Rightarrow x \in S\).
- Quy ước tập rộng là tập con của mọi tập hợp.
– Người ta thường minh hoạ một tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ ven (Hình sau)
– Minh hoạ T là một tập con của S như hình 1.3
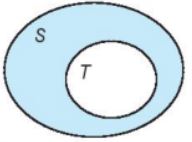
c) Hai tập hợp bằng nhau
| Hai tập hợp S và T được gọi là hai tập hợp bằng nhau nếu mỗi phần tử của T cũng là phần tử của tập hợp S và ngược lại. Kí hiệu S = T |
|---|

Ví dụ: Cho tập hợp:
C = {châu Á; châu Âu; châu Đại Dương; châu Mĩ; châu Nam Cực; châu Phi}.
a) Hãy chỉ ra tính chất đặc trưng cho các phần tử của tập hợp C.
b) Tập hợp C có bao nhiêu phần tử?
Giải
a) Tính chất đặc trưng của các phần tử của tập hợp C: là các châu lục trên Trái đất.
b) Tập hợp C có 6 phần tử.
1.2. Các tập hợp số
a) Mối quan hệ giữa các tập hợp số
– Tập hợp các số tự nhiên N = {0; 1; 2; 3; 4; …}
– Tập hợp các số nguyênZ gồm các số tự nhiên và các số nguyên âm: Z = {…; -3; -2; -1; 0; 1; 2; 3;…}
– Tập hợp các số hữu tỉ Q gồm các số viết được dưới dạng phân số \(\frac{a}{b}\), với a, b \(\in\) Z, b \( \ne \) 0. Số hữu tỉ còn được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
– tập hợp các số thực R gồm các số hữu tỉ. Số vô tỉ là các số thập phân vô hạn không tuần hoàn.
Mối quan hệ giữa các tập hợp số: \(N \subset Z \subset Q \subset R\)
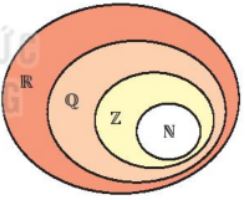
b) Các tập con thường dùng của \(\mathbb{R}\)
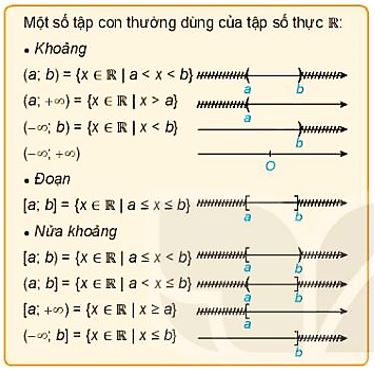
– Kí hiệu \( + \infty \): Đọc là dương vô cực (hoặc dương vô cùng).
– Kí hiệu \( – \infty \): Đọc là âm vô cực (hoặc âm vô cùng).
– a, b gọi là các đầu mút của đoạn, khoảng hay nửa khoảng.
Ví dụ: Cho tập hợp C = {-4; 0; 1; 2}. Các mệnh đề sau đúng hay sai?
a) C là tập con của \(\mathbb{Z}\)
b) C là tập con của \(\mathbb{N}\)
c) C là tập con của \(\mathbb{R}\)
Giải
a) Dễ thấy: \( – 4;{\rm{ }}0;{\rm{ }}1;{\rm{ }}2 \in \mathbb{Z}\)
Vậy C là tập con của \(\mathbb{Z}\), mệnh đề đúng.
b) Vì \( – 4 \notin \mathbb{N}\) nên C không là tập con của \(\mathbb{N}\)
Vậy mệnh đề sai.
c) Dễ thấy: \( – 4;{\rm{ }}0;{\rm{ }}1;{\rm{ }}2 \in \mathbb{R}\)
Vậy C là tập con của \(\mathbb{R}\), mệnh đề đúng.
1.3. Các phép toán trên tập hợp
a) Giao của hai tập hợp
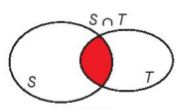
Tập hợp các phần tử thuộc cả hai tập hợp S và T gọi là giao của hai tập hợp S và T, kí hiệu là \(S \cap T\).
\(S \cap T = \{ x|x \in S\) và \(x \in T\} \).
b) Hợp của hai tập hợp
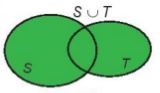
Tập hợp gồm các phần tử thuộc tập hợp S hoặc thuộc tập hợp T gọi là hợp của hai tập hợp S và T, kí hiệu là \(S \cup T\).
\(S \cup T = \{ x|x \in S\) hoặc \(x \in T\} \)
c) Hiệu của hai tập hợp
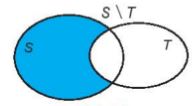
– Hiệu của hai tập hợp S và T là tập hợp gồm các phần tử thuộc S nhưng không thuộc T, kí hiệu là S\T.
S\T = {x | x\(\in\) S và x \(\notin\) T}.
– Nếu \(T \subset S\) thì S\T được gọi là phần bù của T trong S, kí hiệu là CST
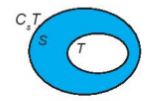
Chú ý: CSS = \(\emptyset \)
Ví dụ: Tìm phần bù của các tập hợp sau trong \(\mathbb{R}\):
a) \(\left( { – \infty ; – 2} \right)\)
b) \([ – 5; + \infty )\)
Giải
Ta có:

Suy ra phần bù của tập hợp \(\left( { – \infty ; – 2} \right)\) trong \(\mathbb{R}\) là: \(\mathbb{R}{\rm{\backslash }}\left( { – \infty ; – 2} \right) = [ – 2; + \infty )\)

Suy ra phần bù của tập hợp \([ – 5; + \infty )\) trong \(\mathbb{R}\) là: \(\mathbb{R}{\rm{\backslash }}[ – 5; + \infty ) = ( – \infty ; – 5)\)
Bài tập minh họa
Câu 1: Tìm tất cả các tập hợp con của tập hợp \(A = \left\{ { 1; 2; 3} \right\}.\)
Hướng dẫn giải
Tập A có 8 tập hợp con là: \(\emptyset ,\left\{ { 1} \right\},\left\{ 2 \right\},\left\{ 3 \right\},\left\{ { 1; 2} \right\},\left\{ {1; 3} \right\},\left\{ {2; 3} \right\},\left\{ { 1; 2; 3} \right\}.\)
Câu 2: Cho \(M = \left\{ {1; 3; 5; 7; 9} \right\}\), \(N = {\rm{\{ }}0;1;2;3;4;5;6\}\), \(P = \left\{ {4;5;6;7;8;9;10} \right\}.\)
Hãy liệt kê các phần tử của các tập hợp dưới đây?
a) \(M \cap (N \cap P);\)
b) \(M \cup (N \cup P);\)
Hướng dẫn giải
a) Ta có: \(N \cap P = \left\{ {4;5;6} \right\}\)
\( \Rightarrow A \cap \left( {B \cap C} \right) = \left\{ {5} \right\}.\)
b) \(N \cup P = \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}\)
\( \Rightarrow A \cup \left( {B \cup C} \right) = \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}.\)
=============
Học Toán lớp 10 – Kết nối – Bài 1. Mệnh đề Toán 10 Kết nối tri thức
