Đề bài
Câu 1: Một hình chóp có 28 cạnh sẽ có bao nhiêu mặt?
A. 14 B. 28
C. 15 D. 42
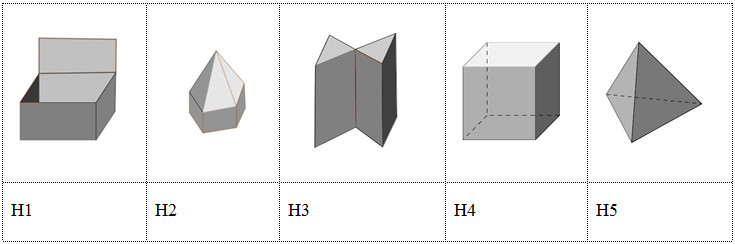
Câu 2 . Những hình nào không phải là khối đa diện?

A. H1 và H3. B. H1 và H2.
C. H2 và H4. D. H3 và H5.
Câu 3: Cho khối chóp S.ABC. Lấy A’, B’ lần lượt thuộc SA, SB sao cho 2SA’ = 3A’A; 3SB’ = B’B. Tỉ số thể tích giữa hai khối chóp S.A’B’C và S.ABC là:
A. \(\dfrac{3}{{20}}\) , B.\(\dfrac{2}{{15}}\) ,
C.\(\dfrac{1}{6}\) , D. \(\dfrac{3}{{10}}\)
Câu 4: thể tích của khối hộp chữ nhật ABCDA’B’C’D’ có AB = a; BC = b; AA’ = c là:
A. \(V = ab+bc+ca\) B. \(V = b^3\)
C. \(V = c^3\) D. \(V = abc\)
Câu 5: Cho khối lăng trụ ABC.A’B’C’ có thể tích là V. Thể tích của khối chóp A’.ABC là:
A. 2V B. \(\dfrac{1}{2}V\)
C. \(\dfrac{1}{3}V\) D. \(\dfrac{1}{6}V\)
Câu 6: Số đỉnh của một hình bát diện đều là:
A. Sáu B. Tám
C. Mười D. Mười hai
Câu 7: Khối chóp có diện tích đáy 4 \(m^2\) và chiều cao 1,5m có thể tích là:
A. \(6 m^3\) B. \(4.5{m^3}\)
C. \(4{m^3}\) D. \(2 m^3\)
Câu 8: Khối chóp tứ giác đều có thể tích \(V = 2{{\rm{a}}^3}\), cạnh đáy bằng \(a\sqrt 6 \) thì chiều cao khối chóp bằng:
A. a. B. \(a\sqrt 6 \)
C. \(\dfrac{a}{3}\) D. \(\dfrac{{a\sqrt 6 }}{3}\)
Câu 9. Cho khối chóp \(S.ABC\)có đáy \(ABC\) là tam giác đều cạnh \(a\). Hai mặt bên \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với đáy. Tính thể tích khối chóp biết \(SC = a\sqrt 3 \)
A. \(\dfrac{{2{a^3}\sqrt 6 }}{9}\) B. \(\dfrac{{{a^3}\sqrt 6 }}{{12}}\)
C. \(\dfrac{{{a^3}\sqrt 3 }}{4}\) D. \(\dfrac{{{a^3}\sqrt 3 }}{2}\)
Câu 10. Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy ABC và (SBC) hợp với đáy (ABC) một góc \(60^o\). Tính thể tích hình chóp
A. \(\dfrac{{{a^3}\sqrt 3 }}{8}\) B. \(\dfrac{{{a^3}\sqrt 3 }}{{12}}\)
C. \(\dfrac{{{a^3}}}{4}\) D. \(\dfrac{{{a^3}\sqrt 3 }}{4}\)
Câu 11. Cho khối chóp \(S.ABCD\)có đáy \(ABCD\) là hình chữ nhật \(AD = 2a,\,AB = a\). Gọi \(H\) là trung điểm của \(AD\) , biết \(SH \bot \left( {ABCD} \right)\). Tính thể tích khối chóp biết \(SA = a\sqrt 5 \).
A. \(\dfrac{{2{a^3}\sqrt 3 }}{3}\) B. \(\dfrac{{4{a^3}\sqrt 3 }}{3}\)
C. \(\dfrac{{4{a^3}}}{3}\) D. \(\dfrac{{2{a^3}}}{3}\)
Câu 12. Cho hình chóp tứ giác có đáy là hình chữ nhật cạnh các cạnh bên có độ dài bằng nhau và bằng . Thể tích khối chóp bằng:
\(A.\,\,\dfrac{{10{a^3}}}{{\sqrt 3 }}\) \(B.\,\,\dfrac{{9{a^3}\sqrt 3 }}{2}\)
\(C.\,\,10{a^3}\sqrt 3 \) \(D.\,\,9{a^3}\sqrt 3 \)
Câu 13. Tổng diện tích các mặt của một hình lập phương bằng \(216.\) Thể tích của khối lập phương đó là:
A.216 B.36
C. 125 D. Đáp án khác
Câu 14: Cho hình chóp đều S.ABCD có cạnh đáy bằng \(a\) và cạnh bên tạo với đáy một góc bằng \({30^0}\). Thể tích của hình chóp S.ABCD là?
A. \(\dfrac{{\sqrt 6 }}{3}{a^3}\) B. \(\dfrac{1}{{18}}{a^3}\)
C. \(\dfrac{{\sqrt 6 }}{{18}}{a^3}\) D. \(\dfrac{{\sqrt 6 }}{6}{a^3}\)
Câu 15: Hình chóp đều S.ABC có cạnh đáy bằng \(a\) và cạnh bên bằng \(3a\). Thể tích hình chóp S.ABC là ?
A.\(\dfrac{{\sqrt {28} }}{4}{a^3}\) B. \(\dfrac{{\sqrt {26} }}{4}{a^3}\)
C. \(\dfrac{{\sqrt 3 }}{{12}}{a^3}\) D. \(\dfrac{{\sqrt {26} }}{{12}}{a^3}\)
Câu 16 . Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a là:
A. \(\dfrac{{{a^3}\sqrt 2 }}{3}\) B. \(\dfrac{{{a^3}\sqrt 3 }}{6}\)
C. \(\dfrac{{{a^3}\sqrt 3 }}{2}\) D. \(\dfrac{{{a^3}\sqrt 3 }}{4}\)
Câu 17. Thể tích \(V\) của khối lập phương \(ABCD.A’B’C’D’\), biết \(AB = 2a\) là:
A. \(6{a^3}\) . B. \(2{a^3}\) .
C. \(\dfrac{{8{a^3}}}{3}\) D. \(8{a^3}\)
Câu 18. Cho lăng trụ \(ABCD.A_1B_1C_1D_1\) , đáy là hình chữ nhật ,AB = a ,\(AD = a\sqrt 3 \). Hình chiếu vuông góc của \(A_1\) trên mp(ABCD) trùng với giao điểm của AC và BD. Góc giữa \((ADD_1A_1)\) và (ABCD) bằng \(60^o\) .Tính thể tích khối lăng trụ đã cho:
A.\(3\sqrt 3 {a^3}\quad \) B. \(\dfrac{{3{a^3}}}{2}\)
C.\(\dfrac{{\sqrt 3 {a^3}}}{2}\) D.\(\dfrac{{\sqrt 3 {a^3}}}{4}\)
Câu19: Số mặt phẳng đối xứng của hình hộp chữ nhật mà không có mặt nào là hình vuông:
A. 6 B. 2
C. 3 D. 4
Câu 20: Hình nào trong các hình sau không phải là hình đa diện?
A. Hình thoi
B. Hình chóp
C. Hình lập phương
D. Hình lăng trụ
Lời giải chi tiết
| Câu | 1 | 2 | 3 | 4 | 5 |
| Đáp án | C | A | A | D | C |
| Câu | 6 | 7 | 8 | 9 | 10 |
| Đáp án | A | D | A | B | A |
| Câu | 11 | 12 | 13 | 14 | 15 |
| Đáp án | C | C | A | C | D |
| Câu | 16 | 17 | 18 | 19 | 20 |
| Đáp án | C | D | B | C | A |
Câu 1
Một hình chóp có 28 cạnh sẽ có 15 cạnh.
Chọn đáp án C.
Câu 2
Chọn đáp án A.
Câu 3
Ta có: \(\left\{ \begin{array}{l}2SA’ = 3AA’ = 3\left( {SA – SA’} \right)\\3SB’ = BB’ = SB – SB’\end{array} \right. \)
\(\Rightarrow \left\{ \begin{array}{l}5SA’ = 3SA\\4SB’ = SB\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}\dfrac{{SA’}}{{SA}} = \dfrac{3}{5}\\\dfrac{{SB’}}{{SB}} = \dfrac{1}{4}\end{array} \right.\)
Khi đó \(\dfrac{{{V_{S.A’B’C’}}}}{{{V_{S.ABC}}}} = \dfrac{{SA’}}{{SA}}.\dfrac{{SB’}}{{SB}} = \dfrac{3}{5}.\dfrac{1}{4} = \dfrac{3}{{20}}\)
Chọn đáp án A.
Câu 4
Thể tích của khối hộp chữ nhật ABCDA’B’C’D’ là \(V = abc\)
Chọn đáp án D.
Câu 5
Ta có: \(V = b.h\)
\({V_{A’.ABC}} = \dfrac{1}{3}.Bh\)
Chọn đáp án C.
Câu 6
Số đỉnh của một hình bát diện đều là 6.
Chọn đáp án A.
Câu 7
Thể tích khối chóp là \(V = \dfrac{1}{3}.4.1,5 = 2\,\left( {{m^3}} \right)\)
Chọn đáp án D.
Câu 8
Diện tích đáy của khối chóp là \(S = \left( {a\sqrt 6 } \right)\left( {a\sqrt 6 } \right) = 6{a^2}\)
Khi đó \(h = \dfrac{{3V}}{S} = \dfrac{{6{a^3}}}{{6{a^2}}} = a\)
Chọn đáp án A.
Câu 9
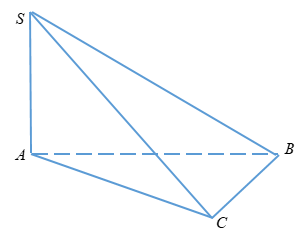
Hai mặt bên \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với đáy
\( \Rightarrow SA \bot \left( {ABC} \right)\)
Áp dụng định lí Py – ta – go ta có:
\(SA = \sqrt {S{C^2} – A{C^2}} = \sqrt {3{a^2} – {a^2}} = a\sqrt 2 \)
Khi đó:
\(V = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.a\sqrt 2 .\dfrac{1}{2}a.a.\sin {60^0} = \dfrac{{{a^3}\sqrt 6 }}{{12}}\)
Chọn đáp án B.
Câu 10
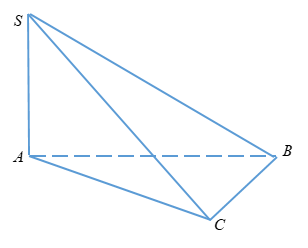
Gọi H là trung điểm của BC
(SBC) hợp với đáy (ABC) một góc 60o
\( \Rightarrow \widehat {SHA} = {60^0}\)
Ta có: \(AH = \sqrt {{a^2} – \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\)
+ \(\tan {60^0} = \dfrac{{SA}}{{AH}} \Rightarrow SA = \dfrac{{3a}}{2}\)
Khi đó: \(V = \dfrac{1}{3}.SA.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{3a}}{2}.\dfrac{1}{2}.a.a.\sin {60^0} = \dfrac{{{a^3}\sqrt 3 }}{8}\)
Chọn đáp án A.
Câu 11
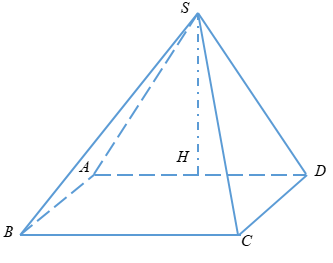
Ta có: \(AH = DH = \dfrac{{AD}}{2} = a\)
Áp dụng định lí Py – ta – go ta có:
\(SH = \sqrt {S{A^2} – A{H^2}} = \sqrt {5{a^2} – {a^2}} = 2a\)
Khi đó ta có:
\(V = \dfrac{1}{3}.SH.{S_{ABCD}} = \dfrac{1}{3}.2a.2a.a = \dfrac{{4{a^3}}}{3}\)
Chọn đáp án C.
Câu 12
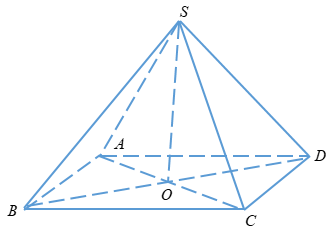
Gọi O là giao điểm của AC và BD
Hình chóp có các cạnh bên bằng nhau nên chân đường vuông góc kẻ từ S xuống mặt phẳng (ABCD) là điểm O
Hay \(SO \bot \left( {ABCD} \right)\)
Ta có: \(BD = \sqrt {A{B^2} + A{C^2}} = \sqrt {9{a^2} + 16{a^2}} = 5a\)
+ \(SO = \sqrt {S{D^2} – O{D^2}} = \sqrt {25{a^2} – \dfrac{{25{a^2}}}{4}} = \dfrac{{5a\sqrt 3 }}{2}\)
Khi đó ta có:
\(V = \dfrac{1}{3}.SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{5a\sqrt 3 }}{2}.3a.4a = 10{a^3}\sqrt 3 \)
Chọn đáp án C.
Câu 13
Chọn đáp án A.
Câu 14
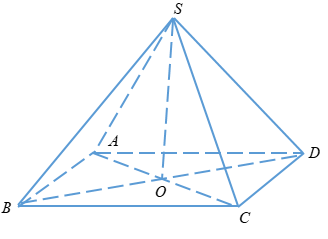
Gọi O là giao điểm của AC và BD
Các mặt bên đều tạp với đáy một góc bằng nhau nên \(SO \bot \left( {ABCD} \right)\)
Ta có: \(BD = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow BO = DO = \dfrac{{a\sqrt 2 }}{2}\)
+ \(\tan {30^0} = \dfrac{{SO}}{{OB}} \Rightarrow SO = \dfrac{{\sqrt 3 }}{3}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{a\sqrt 6 }}{6}\)
Khi đó ta có:
\(V = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{6}.{a^2} = \dfrac{{{a^3}\sqrt 6 }}{{18}}\)
Chọn đáp án C.
Câu 15
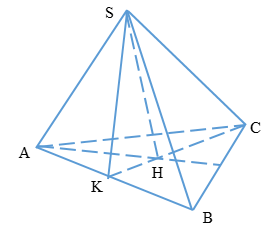
Gọi H là giao điểm của các đường cao trong tam giác ABC
Vì là hình chóp đều nên chân đường cao hạ từ S xuống mặt phẳng (ABC) chính là H
Hay \(SH \bot \left( {ABC} \right)\)
Ta có: \(AH = \dfrac{2}{3}\sqrt {{a^2} – \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{3}\)
\( \Rightarrow SH = \sqrt {S{A^2} – A{H^2}} = \sqrt {9{a^2} – \dfrac{{{a^2}}}{3}} = \dfrac{{a\sqrt {78} }}{3}\)
Khi đó
\(V = \dfrac{1}{3}SH.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{a\sqrt {78} }}{3}.\dfrac{1}{2}.aa\sin {60^0} \)\(\,= \dfrac{{{a^3}\sqrt {26} }}{{12}}\)
Chọn đáp án D.
Câu 16
Diện tích đáy là: \(S = \dfrac{1}{2}a.a\sin {60^0} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Thể tích được xác định: \(V = S.h = \dfrac{{{a^2}\sqrt 3 }}{4}.2a = \dfrac{{{a^3}\sqrt 3 }}{2}\)
Chọn đáp án C.
Câu 17
Thể tích khối lập phương là \(V = {\left( {2a} \right)^3} = 8{a^3}\)
Chọn đáp án D.
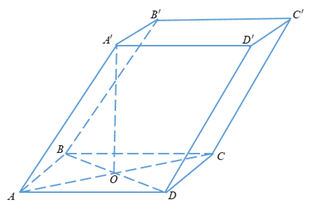
Câu 18
Gọi H là trung điểm của AD
Góc giữa \(\left( {ADD’A’} \right)\)và (ABCD) bằng 600
\( \Rightarrow \widehat {A’HO} = {60^ \circ }\)
Ta có:
\(\tan {60^ \circ } = \dfrac{{A’O}}{{OH}} \Rightarrow AO’ = \tan {60^ \circ }.\dfrac{a}{2} = \dfrac{{a\sqrt 3 }}{2}\)
Vậy \(V = A’O.{S_{ABCD}} = \dfrac{{a\sqrt 3 }}{2}.a.a\sqrt 3 = \dfrac{{3{a^3}}}{2}\)
Chọn đáp án B.
Câu 19
Chọn đáp án C.
Câu 20
Hình thoi không phải là hình đa diện.
Chọn đáp án A.
