I: Phần trắc nghiệm (1 điểm) Chọn chữ cái đứng trước câu trả lời đúng:
Câu 1: Phân số lớn nhất trong các phân số \(\dfrac{4}{{ – 9}};\dfrac{{ – 2}}{9};\dfrac{{ – 7}}{9};\dfrac{5}{{ – 9}}\) là:
A. \(\dfrac{4}{{ – 9}}\) B. \(\dfrac{{ – 2}}{9}\) C. \(\dfrac{{ – 7}}{9}\) D. \(\dfrac{5}{{ – 9}}\)
Câu 2: \(\dfrac{5}{7}\) của 21 bằng:
A. 9 B. 49 C. – 49 D. 21
Câu 3: Nếu Om là tia phân giác \(\widehat {xOy}\) và \(\widehat {xOm} = {60^ \circ }\) thì số đo \(\widehat {xOy}\)là:
A. \({90^ \circ }\) B. \({60^ \circ }\) C. \({30^ \circ }\) D. \({120^ \circ }\)
Câu 4: Tia Oa là tia phân giác của \(\widehat {mOn}\) khi:
A. \(\widehat {mOa} + \widehat {nOa} = \widehat {mOn}\)
B. \(\widehat {mOa} = \widehat {nOa}\)
C. \(\widehat {mOa} = \widehat {nOa} = \dfrac{{\widehat {mOn}}}{2}\)
D. \(\widehat {mOa} + \widehat {nOa} = 2.\widehat {mOn}\)
II: Phần tự luận (9 điểm)
Bài 1: (2 điểm) Thực hiện tính (tính nhanh nếu có thể):
a) \( – 1,6:\left( {1 + \dfrac{3}{5}} \right)\)
b) \( – 90 – \left[ {24 + {{\left( {4 – 12} \right)}^2}} \right]:{\left( { – 2} \right)^3}\)
c) \(1,25.\dfrac{8}{{21}} – 1\dfrac{1}{4}.\dfrac{3}{{21}} + \dfrac{5}{4}.\dfrac{{16}}{{21}}\)
d) \(\dfrac{{{{\left( { – 4} \right)}^3}.\left| { – 3} \right|}}{7}.\left( {\dfrac{{ – 8}}{{13}}:\dfrac{3}{7} + \dfrac{{ – 5}}{{13}}:\dfrac{3}{7}} \right)\)
Bài 2: (2,5 điểm) Tìm x biết
a) \(\dfrac{{ – 3}}{5}x = \dfrac{2}{3}\)
b) \(\left( {3,5 – 3x} \right).1\dfrac{2}{5} = \dfrac{7}{{10}}\)
c) \(\left| {x + \dfrac{1}{3}} \right| – 1 = \dfrac{{{{\left( { – 3} \right)}^2}}}{6}\)
d) \(x + \dfrac{1}{5}x – \dfrac{1}{3}x = \dfrac{{ – 26}}{5}\)
Bài 3: (2 điểm) Sơ kết học kì I, ba lớp 6A, 6B, 6C có tổng số 48 học sinh giỏi. Số học sinh giỏi lớp 6B bằng \(\dfrac{1}{2}\) tổng số, số học sinh giỏi lớp 6A bằng \(\dfrac{3}{8}\) số học sinh còn lại. Tính số học sinh giỏi mỗi lớp.
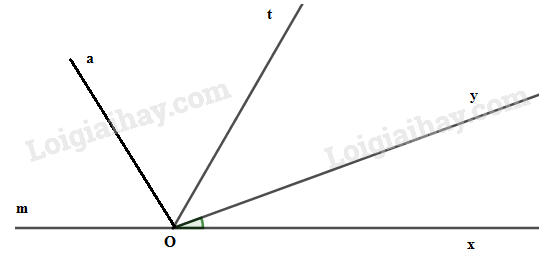
Bài 4: (2 điểm) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ tia Oy và Ot sao cho \(\widehat {xOy} = {20^ \circ }\) và \(\widehat {xOt} = {60^ \circ }\)
a. Tính \(\widehat {yOt}\)
b. Tia Oy có phải là tia phân giác của \(\widehat {xOt}\) không?
c. Gọi Om là tia đối tia Ox. Tính \(\widehat {mOt}.\)
d. Gọi tia Oa là phân giác của \(\widehat {mOt}\). Tính \(\widehat {aOy}.\)
Bài 5: (0,5 điểm) Cho \(S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + … + \dfrac{5}{{{{100}^2}}}.\) Chứng tỏ rằng \(2 < S < 5\).
Lời giải chi tiết
Phần trắc nghiệm
Câu 1: B Câu 2: A Câu 3: D Câu 4: C
Phần tự luận
Bài 1:
Phương pháp:
Thực hiện đúng thứ tự: ngoặc tròn => ngoặc vuông => ngoặc nhọn (\(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\) )
Lũy thừa=> nhân chia => cộng trừ
Lời giải:
a) \( – 1,6:\left( {1 + \dfrac{3}{5}} \right) = \dfrac{{ – 16}}{{10}}:\left( {\dfrac{5}{5} + \dfrac{3}{5}} \right) = \dfrac{{ – 8}}{5}:\dfrac{8}{5} = – 1\)
b)\( – 90 – \left[ {24 + {{\left( {4 – 12} \right)}^2}} \right]:{\left( { – 2} \right)^3} = – 90 – \left( {24 + {8^2}} \right):\left( { – 8} \right)\)\( = – 90 – \left( {24 + 64} \right):\left( { – 8} \right)\) \( = – 90 – 88:\left( { – 8} \right) = – 90 – \left( { – 11} \right) = – 90 + 11 = – 79\)
c) \(1,25.\dfrac{8}{{21}} – 1\dfrac{1}{4}.\dfrac{3}{{21}} + \dfrac{5}{4}.\dfrac{{16}}{{21}} = \dfrac{5}{4}.\dfrac{8}{{21}} – \dfrac{5}{4}.\dfrac{3}{{21}} + \dfrac{5}{4}.\dfrac{{16}}{{21}}\)
\( = \dfrac{5}{4}\left( {\dfrac{8}{{21}} – \dfrac{3}{{21}} + \dfrac{{16}}{{21}}} \right) = \dfrac{5}{4}\left( {\dfrac{{8 – 3 + 16}}{{21}}} \right)\) \( = \dfrac{5}{4}.\dfrac{{21}}{{21}} = \dfrac{5}{4}.1 = \dfrac{5}{4}\)
d) \(\dfrac{{{{\left( { – 4} \right)}^3}.\left| { – 3} \right|}}{7}.\left( {\dfrac{{ – 8}}{{13}}:\dfrac{3}{7} + \dfrac{{ – 5}}{{13}}:\dfrac{3}{7}} \right)\)\( = \dfrac{{\left( { – 64} \right).3}}{7}.\left( {\dfrac{{ – 8}}{{13}}.\dfrac{7}{3} + \dfrac{{ – 5}}{{13}}.\dfrac{7}{3}} \right) = \dfrac{{\left( { – 64} \right).3}}{7}.\left( {\dfrac{{ – 8}}{{13}} + \dfrac{{ – 5}}{{13}}} \right).\dfrac{7}{3}\)
\( = \dfrac{{\left( { – 64} \right).3}}{7}.\left( {\dfrac{{ – 13}}{{13}}} \right).\dfrac{7}{3} = \dfrac{{\left( { – 64} \right).3}}{7}.\dfrac{7}{3}.\left( { – 1} \right) = \dfrac{{\left( { – 64} \right).3.7.\left( { – 1} \right)}}{{7.3}} = 64\)
Bài 2:
Phương pháp:
Sử dụng các qui tắc chuyển vế đưa về dạng tìm \(x\) quen thuộc
Sử dụng \(\left| a \right| = \left\{ \begin{array}{l}a\,khi\,a \ge 0\\ – a\,\,khi\,a < 0\end{array} \right.\)
Lời giải:
a) \(\dfrac{{ – 3}}{5}x = \dfrac{2}{3}\)
\(x = \dfrac{2}{3}:\left( { – \dfrac{3}{5}} \right)\)
\(x = \dfrac{2}{3}.\left( {\dfrac{{ – 5}}{3}} \right)\)
\(x = – \dfrac{{10}}{9}\)
b)
\(\begin{array}{l}\left( {3,5 – 3x} \right).1\dfrac{2}{5} = \dfrac{7}{{10}}\\\left( {3,5 – 3x} \right).\dfrac{7}{5} = \dfrac{7}{{10}}\\3,5 – 3x = \dfrac{7}{{10}}:\dfrac{7}{5}\\\dfrac{7}{2} – 3x = \dfrac{7}{{10}}.\dfrac{5}{7}\\\dfrac{7}{2} – 3x = \dfrac{1}{2}\\3x = \dfrac{7}{2} – \dfrac{1}{2}\\3x = 6\\x = 2\end{array}\)
c)
\(\begin{array}{l}\left| {x + \dfrac{1}{3}} \right| – 1 = \dfrac{{{{\left( { – 3} \right)}^2}}}{6}\\\left| {x + \dfrac{1}{3}} \right| – 1 = \dfrac{9}{6}\\\left| {x + \dfrac{1}{3}} \right| = \dfrac{3}{2} + 1\\\left| {x + \dfrac{1}{3}} \right| = \dfrac{5}{2}\end{array}\)
Trường hợp 1:
\(\begin{array}{l}x + \dfrac{1}{3} = \dfrac{5}{2}\\x = \dfrac{5}{3} – \dfrac{1}{2} = \dfrac{7}{6}\end{array}\)
Trường hợp 2:
\(\begin{array}{l}x + \dfrac{1}{3} = – \dfrac{5}{2}\\x = \dfrac{{ – 5}}{2} – \dfrac{1}{3} = \dfrac{{ – 17}}{6}\end{array}\)
d) \(x + \dfrac{1}{5}x – \dfrac{1}{3}x = \dfrac{{ – 26}}{5}\)
\(\begin{array}{l}x\left( {1 + \dfrac{1}{5} – \dfrac{1}{3}} \right) = \dfrac{{ – 26}}{5}\\x.\dfrac{{13}}{{15}} = \dfrac{{ – 26}}{5}\\x = – 6\end{array}\)
Bài 3:
Phương pháp:
Sử dụng ba bài toán cơ bản của phân số
Lời giải:
Số học sinh giỏi lớp \(6B\) là \(48.\dfrac{1}{2} = 24\) học sinh
Số học sinh giỏi hai lớp 6A và 6C là \(48 – 24 = 24\) học sinh
Số học sinh giỏi lớp 6A bằng \(\dfrac{3}{8}.24 = 9\) học sinh
Số học sinh giỏi lớp 6C là \(24 – 9 = 15\) học sinh
Bài 4:
Phương pháp:
Sử dụng công thức cộng góc và tính chất tia phân giác của một góc.
Lời giải:

a) Vì \(\widehat {xOy} < \widehat {xOt}\,\left( {20^\circ < 60^\circ } \right)\) nên tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Ot\)
Suy ra \(\widehat {xOy} + \widehat {yOt} = \widehat {xOt}\) hay \(20^\circ + \widehat {yOt} = 60^\circ \) nên \(\widehat {yOt} = 60^\circ – 20^\circ = 40^\circ \)
b) Vì \(\widehat {xOy} < \widehat {yOt}\,\left( {20^\circ < 40^\circ } \right)\) nên tia \(Oy\) không phải tia phân giác của \(\widehat {xOt}\)
c) Ta có \(\widehat {xOt} + \widehat {mOt} = 180^\circ \) (hai góc kề bù) nên \(\widehat {mOt} = 180^\circ – \widehat {xOt} = 180^\circ – 60^\circ = 120^\circ \)
d) Ta có \(\widehat {aOt} = \dfrac{{\widehat {mOt}}}{2} = \dfrac{{120^\circ }}{2} = 60^\circ \) (do \(Oa\) là phân giác \(\widehat {mOt}\) )
Vì \(Oy\) nằm giữa \(Ot\) và \(Oz\); \(Oa\) nằm giữa tia \(Ot\) và \(Om\) mà \(\widehat {xOt}\) và \(\widehat {tOm}\) là hai góc kề bù nên tia \(Ot\) nằm giữa hai tia \(Oa\) và \(Oy\) .
Suy ra \(\widehat {tOy} + \widehat {aOt} = \widehat {aOy}\) hay \(\widehat {aOy} = 40^\circ + 60^\circ = 100^\circ .\)
Bài 5:
Phương pháp:
Chỉ ra S>2 và S<5 để suy ra điều cần chứng minh
Lời giải:
Ta có:
\(\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + … + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + … + \dfrac{1}{{100.100}}} \right)\\ > 5.\left( {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + … + \dfrac{1}{{100.101}}} \right)\\ > 5.\left( {\dfrac{1}{2} – \dfrac{1}{3} + \dfrac{1}{3} – \dfrac{1}{4} + … + \dfrac{1}{{100}} – \dfrac{1}{{101}}} \right)\\ > 5.\left( {\dfrac{1}{2} – \dfrac{1}{{101}}} \right) > \dfrac{5}{2} > 2\\ \Rightarrow S > 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\end{array}\)
\(\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + … + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + … + \dfrac{1}{{100.100}}} \right)\\ < 5.\left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + … + \dfrac{1}{{99.100}}} \right)\\ < 5.\left( {1 – \dfrac{1}{2} + \dfrac{1}{2} – \dfrac{1}{3} + \dfrac{1}{3} – \dfrac{1}{4} + … + \dfrac{1}{{99}} – \dfrac{1}{{100}}} \right)\\ < 5.\left( {1 – \dfrac{1}{{100}}} \right) < 5\\ \Rightarrow S < 5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) : \(2 < S < 5\) (đpcm).
