Đề bài
Câu 1 (2.5 điểm). Cho phương trình \(m{x^2} – 2\left( {m – 1} \right)x + m – 3 = 0\)
a) Giải phương trình khi \(m = 3\).
b) Tìm m để phương trình trên có hai nghiệm \({x_1};{x_2}\) thỏa mãn: \({x_1} + 2{x_2} = 1\).
Câu 2 (2.5 điểm). Giải các phương trình sau:
a) \(\sqrt {3{x^2} – 4x + 77} = 2x + 5\)
b) \({x^2} – x + \sqrt {x + 1} – 8 = 0\)
Câu 3 (1,0 điểm). Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 4\\x\left( {x + y + 1} \right) + y\left( {y + 1} \right) = 2\end{array} \right.{\rm{ }}\)\(\;\left( {x;y \in R} \right)\)
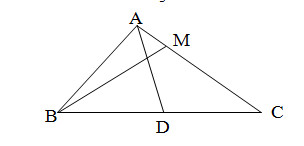
Câu 4 (1,0 điểm). Cho tam giác \(ABC\) có \(\angle BAC = {60^0};AB = 5;AC = 10\). Gọi \(D\)là trung điểm \(BC\) và \(M\)là điểm thỏa mãn \(3M\vec A + 2M\vec C = \vec 0\).
Tính độ dài \(BM\) và chứng minh rằng \(AD \bot BM\).
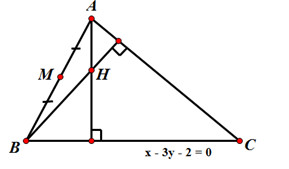
Câu 5 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trực tâm H(3; -2) và trung điểm của AB là \(M\left( {\dfrac{1}{2};0} \right)\). Đường thẳng BC có phương trình x – 3y – 2 = 0. Xác định tọa độ các đỉnh của tam giác ABC.
Câu 6(1,0 điểm). Cho \(x;y;z\) là các số thực dương thỏa mãn : \(x + y + z = 3\)
Tìm giá trị lớn nhất của biểu thức \(P = \dfrac{x}{{2x + y + z}} + \dfrac{y}{{x + 2y + z}} \)\(\,+ \dfrac{z}{{x + y + 2z}}\)
Câu 7(1,0 điểm). Cho \(a,\,b,\,c\) là độ dài ba cạnh của một tam giác không nhọn.
Chứng minh rằng \(\left( {{a^2} + {b^2} + {c^2}} \right)\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right) \ge 10\)
Lời giải chi tiết
Câu 1:
a. Giải phương trình khi \(m = 3\).
Khi \(m = 3\) phương trình trở thành: \(3{x^2} – 4x = 0\)
\( \Leftrightarrow x\left( {3x – 4} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{4}{3}\end{array} \right.\)
Kết luận: Nghiệm của phương trình là \(x = 0\) và \(x = \dfrac{4}{3}\)
b. Tìm m để phương trình trên có hai nghiệm \({x_1};{x_2}\) thỏa mãn: \({x_1} + 2{x_2} = 1\).
Để phương trình có hai nghiệm \({x_1};{x_2}\) thì \(\left\{ \begin{array}{l}m \ne 0\\\Delta \ge 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\{\left( {m – 1} \right)^2} – m\left( {m – 3} \right) \ge 0\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m + 1 \ge 0\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ge – 1\end{array} \right.\) (*)
Áp dụng Vi-et và giả thiết ta có hệ \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2 – \dfrac{2}{m}\left( 1 \right)\\{x_1} + 2{x_2} = 1\left( 2 \right)\\{x_1}{x_2} = 1 – \dfrac{3}{m}\left( 3 \right)\end{array} \right.\)
Từ (1) và (2) suy ra \({x_2} = – 1 + \dfrac{2}{m};{x_1} = 3 – \dfrac{4}{m}\) (4)
Thế (4) vào (3) được
\(\begin{array}{l}\left( { – 1 + \dfrac{2}{m}} \right)\left( {3 – \dfrac{4}{m}} \right) = 1 – \dfrac{3}{m} \\\Leftrightarrow 4{m^2} – 13m + 8 = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{{13 – \sqrt {41} }}{8}\\m = \dfrac{{13 + \sqrt {41} }}{8}\end{array} \right.\end{array}\).
Kết hợp điều kiện (*) suy ra \(\left[ \begin{array}{l}m = \dfrac{{13 – \sqrt {41} }}{8}\\m = \dfrac{{13 + \sqrt {41} }}{8}\end{array} \right.\)
Câu 2:
a) Giải phương trình \(\sqrt {3{x^2} – 4x + 77} = 2x + 5\)
Phương trình \( \Leftrightarrow \left\{ \begin{array}{l}2x + 5 \ge 0\\3{x^2} – 4x + 77 = {\left( {2x + 5} \right)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge – \dfrac{5}{2}\\{x^2} + 24x – 52 = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \ge – \dfrac{5}{2}\\\left[ \begin{array}{l}x = 2\\x = – 26\end{array} \right.\end{array} \right. \Leftrightarrow x = 2\)
Nghiệm của phương trình là \(x = 2\)
b) Giải phương trình \({x^2} – x + \sqrt {x + 1} – 8 = 0\).(1)
ĐKXĐ: \(x \ge – 1\)
(1) \( \Leftrightarrow \left( {{x^2} – x – 6} \right) + \left( {\sqrt {x + 1} – 2} \right) = 0\)
\( \Leftrightarrow \left( {x – 3} \right)\left( {x + 2} \right) + \dfrac{{x – 3}}{{\sqrt {x + 1} + 2}} = 0\)
\( \Leftrightarrow \left( {x – 3} \right)\left[ {x + 2 + \dfrac{1}{{\sqrt {x + 1} + 2}}} \right] = 0\)
\( \Leftrightarrow x = 3\)( vì \(x + 2 + \dfrac{1}{{\sqrt {x + 1} + 2}} > 0,\forall x \ge – 1\))
Câu 3: Giải hệ phương trình\(\left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 4\\x\left( {x + y + 1} \right) + y\left( {y + 1} \right) = 2\end{array} \right.\)(I)
Hệ \(\left( I \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 4\\{x^2} + {y^2} + x + y + xy = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( {x + y} \right)^2} – 2xy + x + y = 4\\{\left( {x + y} \right)^2} – xy + x + y = 2\end{array} \right.\)
Đặt \(S = x + y;P = xy\)(đk:\({S^2} \ge 4P)\)
Hệ (I) trở thành \(\left\{ \begin{array}{l}{S^2} – 2P + S = 4\\{S^2} – P + S = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}P = – 2\\\left[ \begin{array}{l}S = 0\\S = – 1\end{array} \right.\end{array} \right.\)
Với \(S = 0,P = – 1\)(thỏa mãn). Giải hệ được \(\left( {x;y} \right) = \left( {\sqrt 2 ; – \sqrt 2 } \right),\) \(\left( {x;y} \right) = \left( { – \sqrt 2 ;\sqrt 2 } \right)\)
Với \(S = – 1,P = – 2\)(thỏa mãn).
Giải hệ được \(\left( {x;y} \right) = \left( {1; – 2} \right),\left( {x;y} \right) = \left( { – 2;1} \right)\)
Kết luận: Vậy hệ có 2 nghiệm \(\left( {x;y} \right) = \left( {1; – 2} \right),\left( {x;y} \right) = \left( { – 2;1} \right)\)
Câu 4:
Từ giả thiết suy ra \(AM = \dfrac{2}{5}AC = 4\)

Áp dụng định lý côsin vào \(\Delta ABM\) được \(B{M^2} = A{B^2} + A{M^2} – 2AB.AM.\cos BAM = 21 \) \(\Leftrightarrow BM = \sqrt {21} \)
\(\eqalign{
& \overrightarrow {AD} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right); \cr
& \overrightarrow {BM} = \overrightarrow {AM} – \overrightarrow {AB} = \frac{2}{5}\overrightarrow {AC} – \overrightarrow {AB} \cr} \)
\(\eqalign{
& 2\overrightarrow {AD} .5\overrightarrow {BM} = \left( {\overrightarrow {AB} + \overrightarrow {AC} .} \right)\left( {2\overrightarrow {AC} – 5\overrightarrow {AB} } \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = – 5A{B^2} + 2A{C^2} – 3\overrightarrow {AC} .\overrightarrow {AB} = 0 \cr} \)
Vậy \(AD \bot BM\)
Câu 5:
– Phương trình AH: \(3(x – 3) + 1.(y + 2) = 0\)
\( \Leftrightarrow 3x + y – 7 = 0\)
Do \(A \in AH;B \in BC.\) Đặt \(A({x_1};7 – 3{x_1});B({x_2};\dfrac{{{x_2} – 2}}{3}).\)
M là trung điểm AB \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 1}\\{(7 – 3{x_1}) + \dfrac{{{x_2} – 2}}{3} = 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_1} = 2}\\{{x_2} = – 1}\end{array}} \right.\) \(\Rightarrow\) A(2; 1); B(-1; -1).
Đặt \(C({x_3};\dfrac{{{x_3} – 2}}{3}).\) Có : \(\overrightarrow {AC} = \left( {{x_3} – 2;\dfrac{{{x_3} – 2}}{3} – 1} \right);\) \(\;\overrightarrow {BH} = (4; – 1)\)
Vì \(BH \bot AC \Leftrightarrow \overrightarrow {BH} .\overrightarrow {AC} = 0\)
\( \Leftrightarrow 4({x_3} – 2) – 1.\dfrac{{{x_3} – 5}}{3} = 0\) \( \Leftrightarrow {x_3} = \dfrac{{19}}{{11}}\) \( \Rightarrow \)\(C\left( {\dfrac{{19}}{{11}}; – \dfrac{1}{{11}}} \right)\).
Vậy A(2; 1); B(-1; -1); \(C\left( {\dfrac{{19}}{{11}}; – \dfrac{1}{{11}}} \right)\).
Câu 6:
\(P = \dfrac{x}{{x + 3}} + \dfrac{y}{{y + 3}} + \dfrac{z}{{z + 3}}\)\(\, = 3 – 3\left( {\dfrac{1}{{x + 3}} + \dfrac{1}{{y + 3}} + \dfrac{1}{{z + 3}}} \right)\)
Ta có \(\left[ {\left( {x + 3} \right) + \left( {y + 3} \right) + \left( {z + 3} \right)} \right]\left( {\dfrac{1}{{x + 3}} + \dfrac{1}{{y + 3}} + \dfrac{1}{{z + 3}}} \right) \ge 9\)
\( \Leftrightarrow \dfrac{1}{{x + 3}} + \dfrac{1}{{y + 3}} + \dfrac{1}{{z + 3}} \ge \dfrac{3}{4}\)
\( \Rightarrow P \le \dfrac{3}{4}\), dấu “=” xảy ra khi x = y = z = 1
Vậy GTLN của P là \(\dfrac{3}{4}\)khi x = y = z = 1
Câu 7: Do \(a,\,b,\,c\) là độ dài ba cạnh của một tam giác không nhọn nên có một trong các bất đẳng thức sau xảy ra: \({a^2} \ge {b^2} + {c^2},\,\,{b^2} \ge {c^2} + {a^2},{c^2} \ge {a^2} + {b^2}\). Giả sử \({a^2} \ge {b^2} + {c^2}\). Đặt \(A = \left( {{a^2} + {b^2} + {c^2}} \right)\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right)\)
Khi đó ta có:
\(\left( {{a^2} + {b^2} + {c^2}} \right)\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right)\)\(\, = 1 + {a^2}\left( {\dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right) + \dfrac{{{b^2} + {c^2}}}{{{a^2}}} + \left( {{b^2} + {c^2}} \right)\left( {\dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}} \right)\)
\( \Leftrightarrow A \ge 1 + {a^2}.\dfrac{4}{{{b^2} + {c^2}}} + \dfrac{{{b^2} + {c^2}}}{{{a^2}}} + 4\)
\( \Leftrightarrow A \ge 1 + \dfrac{{3a{}^2}}{{{b^2} + {c^2}}} + \dfrac{{a{}^2}}{{{b^2} + {c^2}}} + \dfrac{{{b^2} + {c^2}}}{{a{}^2}} + 4 \)\(\,\ge 1 + 3 + 2\sqrt {\dfrac{{a{}^2}}{{{b^2} + {c^2}}}.\dfrac{{{b^2} + {c^2}}}{{a{}^2}}} + 4 = 10\)
Dấu “=” xảy ra khi tam giác ABC vuông cân tại A
