I. Phương pháp giải
- Đặt các diện tích cần tìm bởi các ẩn rồi đưa về phương trình hoặc hệ phương trình với các ẩn đó.
- Giải phương trình hoặc hệ phương trình để tìm nghiệm bài toán .
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Bài 1: Cho $\triangle ABC$ có diện tích bằng đơn vị, trên cạnh AB lấy M và trên AC lấy N sao cho AM = 3BM. BN cắt CM ở O.
Tính diện tích của $\triangle AOB$.
Đặt $S_{AOB} = x; S_{AOC} = y$ (x,y > 0)
Vì AM = 3BM => $\frac{AM}{AB}=\frac{3}{4}$
=> $\frac{S_{OAM}}{S_{OAB}}=\frac{3}{4}$
=> $S_{OAM}=\frac{3x}{4}$
Tương tự , ta có :
$\frac{AN}{AC}=\frac{4}{5}$ => $\frac{S_{OAN}}{S_{OAC}}=\frac{4}{5}$
=> $S_{OAN}=\frac{4y}{5}$
Ta có : $S_{BAN}= S_{BAO} + S_{OAN} = x + \frac{4y}{5}$
Mà : $S_{BAN}= \frac{4}{5}S_{ABC}=\frac{4}{5}$
<=> $x+\frac{4y}{5}=\frac{4}{5}$ (1)
+ $S_{CAM}= S_{COA} + S_{OAM} = y + \frac{3x}{4}$
Mà : $S_{CAM}= \frac{3}{4}S_{ABC}=\frac{3}{4}$
<=> $y+\frac{3x}{4}=\frac{3}{4}$ (2)
Từ (1) , (2) => $\left\{\begin{matrix}5x+4y=4 (*) & \\ 3x+4y=3 (**) & \end{matrix}\right.$
Lấy (*) – (**) ta được : $x=\frac{1}{2}$
Thay $x=\frac{1}{2}$ vào (*) ta được : $y=\frac{3}{8}$ .
Vậy $S_{AOB}=\frac{1}{2}$ và $S_{AOC}=\frac{3}{8}$ .
Bài 2: Giả sử MNPQ là hình vuông nội tiếp tam giác ABC, với $M\in AB;N\in AC; P,Q\in BC$ .
Tính cạnh hình vuông biết BC = a và đường cao AH = h .
Gọi I là giao điểm của AH với MN.
Đặt cạnh hình vuông MNPQ là x (x > 0)
Ta có: $S_{AMN}=\frac{1}{2}MN.AI=\frac{1}{2}x(h-x)$
$S_{BMNC}=\frac{1}{2}(BC+MN).MQ=\frac{1}{2}(a+x)x$
$S_{ABC}=\frac{1}{2}a.h$
Mặt khác , ta lại có : $S_{ABC}=S_{AMN}+S_{BMNC}$
<=> $\frac{1}{2}a.h=\frac{1}{2}x(h-x)+\frac{1}{2}x(a+x)$
<=> $a.h=x(a+h)=> x=\frac{a.h}{a+h}$
Vậy cạnh hình vuông MNPQ là $\frac{a.h}{a+h}$ .
Bài 4: Một tam giác có độ dài các đường cao là các số nguyên và bán kính đường tròn ngoại tiếp bằng 1.
Chứng minh tam giác đó đều.
Đặt a = BC, b = AC, c = AB.
Gọi x, y, z lần lượt là độ dài các đường cao tương ứng với 3 cạnh a, b, c của tam giác.
Vì bán kính đường tròn nội tiếp bằng 1 => x, y, z > 2 .
Giả sử : $x \geq y \geq z \geq 2$
Theo kết quả bài 3( ở trên ): $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\leq \frac{3}{z}$
=> $z\leq 3=> z=3$ .
Từ : $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1 => \frac{1}{x}+\frac{1}{y}=\frac{2}{3}$
<=> 3( x + y ) = 2xy .
=> (2x – 3 )(2y – 3 ) = 9 = 3.3 = 9.1
=> Hoặc x = 3 , y = 3 hoặc x = 6 , y = 2
Mà ta có $y\geq z(z=3)$
=> x = 6 , y= 2 (loại).
=> x = y = z = 3 <=> a = b = c.
Vậy tam giác đó là tam giác đều ( đpcm ).
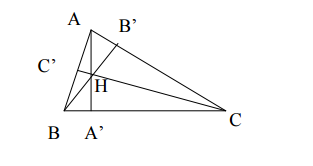
Bài 5: Cho $\triangle ABC$ có 3 góc nhọn, các đường cao AA‟ , BB‟ , CC‟ và trực tâm H.
Tính tổng: $\frac{HA{}’}{AA{}’}+\frac{HB{}’}{BB{}’}+\frac{HC{}’}{CC{}’}$ .
Ta có : $\frac{S_{HBC}}{S_{ABC}}=\frac{\frac{1}{2}HA{}’.BC}{\frac{1}{2}AA{}’.BC}=\frac{HA{}’}{AA{}’}$ (1)
$\frac{S_{HAB}}{S_{ABC}}=\frac{\frac{1}{2}HC{}’.AB}{\frac{1}{2}CC{}’.AB}=\frac{HC{}’}{CC{}’}$ (2)
$\frac{S_{HAC}}{S_{ABC}}=\frac{\frac{1}{2}HB{}’.AC}{\frac{1}{2}BB{}’.AC}=\frac{HB{}’}{BB{}’}$ (3)
Cộng (1) + (2) + (3) theo vế ta được :
$\frac{HA{}’}{AA{}’}+\frac{HB{}’}{BB{}’}+\frac{HC{}’}{CC{}’}=\frac{S_{HBC}+S_{HAB}+S_{HAC}}{S_{ABC}}$
<=> $\frac{S_{ABC}}{S_{ABC}}=1$ .
Vậy $\frac{HA{}’}{AA{}’}+\frac{HB{}’}{BB{}’}+\frac{HC{}’}{CC{}’}=1$ .
Bài học cùng chương bài
- Chuyên đề 5: Hình học
- Chuyên đề 4: Giải bài toán bằng cách lập phương trình,hệ phương trình và các bài toán thực tế
- CHUYÊN ĐỀ 3: HÀM SỐ VÀ ĐỒ THỊ
- Chuyên đề 2 : Phương trình bậc hai – Hệ thức Vi-ét và ứng dụng
- Chuyên đề 1: Rút gọn, tính giá trị của biểu thức
- Chuyên đề Bài toán Dựng hình
- Chuyên đề Diện tích đa giác
- Chuyên đề Phương pháp vectơ
- Chuyên đề Tam thức bậc hai – Toán 9
- Chuyên đề Phương pháp đặt ẩn phụ đưa về hệ phương trình
- Chuyên đề Ứng dụng nghiệm phương trình bậc hai
- Chuyên đề Phương trình, hệ phương trình bậc nhất
- Chuyên đề Rút gọn phân thức đại số
- Chuyên đề Vận dụng bất đẳng thức Cô si để tìm cực trị
Trả lời