Sách Toán - Học toán
Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán
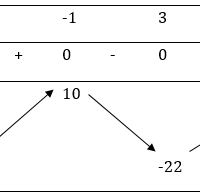
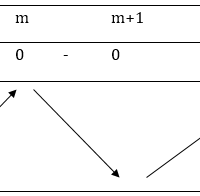
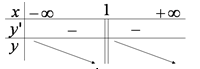
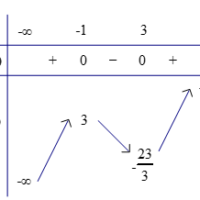
Dạng 1: Tìm GTLN và GTNN của hàm số trên miền D Ví dụ : Tìm GTLN-GTNN của các hàm số sau: a) Hàm số \(y=x^3-3x^2-9x+5\). b) Hàm số \(y=\frac{x^2+2x+3}{x-1},x\in(1;3].\) c. $y = \frac{{x + \sqrt {1 + 9{x^2}} }}{{8{x^2} + 1}}$ trên khoảng $\left( {0; + \infty } \right).$ Lời giải: a) Hàm số \(y=x^3-3x^2-9x+5\). … [Đọc thêm...] vềVí dụ Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Sách giáo khoa Bài 2. Cực trị của hàm số – Giải tích 12 cơ bản ==== … [Đọc thêm...] vềSách giáo khoa Bài 2. Cực trị của hàm số – Giải tích 12 cơ bản
Sách giáo khoa Bài 1. Sự đồng biến, nghịch biến của hàm số - Giải tích 12 cơ bản ==== … [Đọc thêm...] vềSách giáo khoa Bài 1. Sự đồng biến, nghịch biến của hàm số – Giải tích 12 cơ bản
Tìm tham số m để hàm số đơn điệu trên một miền Ta xét dạng toán tìm điều kiện của tham số $m$ để hàm số đơn điệu trên $R$ hoặc trên khoảng con của $R.$ Lý thuyết: Cho hàm số $y = f\left( {x,m} \right)$ với $m$ là tham số xác định trên một khoảng $I.$ a. Hàm số đồng biến trên $I$ $ \Leftrightarrow y’ \ge 0, \forall x \in I$ và $y’ = 0$ chỉ xảy ra tại hữu hạn điểm. b. … [Đọc thêm...] vềTìm tham số m để hàm số đơn điệu trên một miền
Đồng biến, nghịch biến của hàm số khác Các bước xét tính đơn điệu của hàm số Bước 1 : Tìm tập xác định Bước 2: Tính đạo hàm \(f'(x)=0\). Tìm các điểm \(x_i\) (i= 1 , 2 ,…, n) mà tại đó đạo hàm bằng 0 hoặc không xác định. Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên. Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến … [Đọc thêm...] vềĐồng biến, nghịch biến của hàm số khác
Đồng biến, nghịch biến của hàm số trùng phương Các bước xét tính đơn điệu của hàm số Bước 1 : Tìm tập xác định Bước 2: Tính đạo hàm \(f'(x)=0\). Tìm các điểm \(x_i\) (i= 1 , 2 ,…, n) mà tại đó đạo hàm bằng 0 hoặc không xác định. Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên. Bước 4: Nêu kết luận về các khoảng đồng biến, … [Đọc thêm...] vềĐồng biến, nghịch biến của hàm số trùng phương
Tìm cực trị của hàm số không có tham số Ví dụ 1: Tìm các điểm cực trị của các hàm số sau: a) \(y = \frac{1}{3}{x^3} – {x^2} – 3x + \frac{4}{3}\) b) \(y = \left| x \right|\left( {x + 2} \right)\) Lời giải: a) \(y = \frac{1}{3}{x^3} – {x^2} – 3x + \frac{4}{3}\) Cách 1: Hàm số có TXĐ: \(D=\mathbb{R}\) \(y’ = {x^2} – 2x – 3\) \(y’ = 0 … [Đọc thêm...] vềVí dụ minh họa Cực trị của hàm số
Đồng biến, nghịch biến của hàm số bậc ba, không chứa tham số. VD 1: Tìm khoảng đơn điệu của hàm số $y = {x^3} – 6{x^2} + 9x – 3.$ TXĐ: $D = R.$ Ta có: ${\rm{y’}} = {\rm{3}}{{\rm{x}}^{\rm{2}}}–{\rm{12x}} + {\rm{9}}.$ ${\rm{y’}} = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\\ x = 3 \end{array} \right.$ Giới hạn: $\mathop {\lim }\limits_{x \to – \infty } y = – … [Đọc thêm...] vềĐồng biến, nghịch biến của hàm số bậc ba
A. Kiến thức cơ bản. Các căn bậc hai của số thực \(a<0\) là \(\pm i\sqrt a.\) Xét phương trình bậc hai \(ax^2 + bx + c = 0\) với \(a,b,c\in \mathbb{R},a\ne0.\) Đặt \(\Delta=b^2-4ac\): Nếu \(\Delta=0\) thì phương trình có một nghiệm kép (thực) \(x=-\frac{b}{2a}.\) Nếu \(\Delta>0\) thì phương trình có hai nghiệm thực \(x_{1,2}=\frac{-b\pm \sqrt … [Đọc thêm...] vềChuyên đề: PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
Giải bài tập Sách Bài Tập Đại số 10 theo sách BT cơ bản. MỤC LỤC CHƯƠNG I: MỆNH ĐỀ TẬP HỢP Giải SBT Bài 1: Mệnh đề chương 1 đại số 10 Giải SBT Bài 2: Tập hợp chương 1 đại số 10 Giải SBT Bài 3: Các phép toán tập hợp chương 1 đại số 10 Giải SBT bài 4: Các tập hợp số chương 1 đại số 10 Giải SBT Bài 5: Số gần đúng. Sai số chương 1 đại số 10 Giải SBT … [Đọc thêm...] vềGiải bài tập Sách Bài Tập Đại số 10
