Bài 41
a) \(y = 2x\left( {1 – {x^{ – 3}}} \right);\) b) \(y = 8x – {2 \over {{x^{{1 \over 4}}}}};\)
c) \(y = {x^{{1 \over 2}}}\sin \left( {{x^{{3 \over 2}}} + 1} \right);\) d) \(y = {{\sin \left( {2x + 1} \right)} \over {{{\cos }^2}\left( {2x + 1} \right)}};\)
Giải
a) \(\int {2x\left( {1 – {x^{ – 3}}} \right)} dx = \int {\left( {2x – 2{x^{ – 2}}} \right)dx = {x^2} + {2 \over x} + C} \)
b) \(\int {\left( {8x – {2 \over {{x^{{1 \over 4}}}}}} \right)dx = } \int {\left( {8x – 2{x^{ – {1 \over 4}}}} \right)} dx = 4{x^2} – {8 \over 3}{x^{{3 \over 4}}} + C\)
c) Đặt
\(\eqalign{
& u = {x^{{3 \over 2}}} + 1 \Rightarrow du = {3 \over 2}{x^{{1 \over 2}}}dx \Rightarrow {x^{{1 \over 2}}}dx = {2 \over 3}du \cr
& \int {{x^{{1 \over 2}}}\sin\left( {{x^{{3 \over 2}}} + 1} \right)dx = {2 \over 3}\int {\sin udu = – {2 \over 3}\cos u + C = – {2 \over 3}\cos \left( {{x^{{3 \over 2}}} + 1} \right)} + C} \cr} \)
d) Đặt \(u = \cos \left( {2x + 1} \right) \Rightarrow du = – 2\sin \left( {2x + 1} \right)dx \Rightarrow \sin \left( {2x + 1} \right)dx = – {1 \over 2}du\)
Do đó \(\int {{{\sin \left( {2x + 1} \right)} \over {{{\cos }^2}\left( {2x + 1} \right)}}} dx = – {1 \over 2}\int {{{du} \over {{u^2}}} = {1 \over {2u}} + C = {1 \over {2\cos \left( {2x + 1} \right)}}} + C\)
———————————————————–
Bài 42
a) \(y = {1 \over {{x^2}}}\cos \left( {{1 \over x} – 1} \right)\); b) \(y = {x^3}{\left( {1 + {x^4}} \right)^3}\);
c) \(y = {{x{e^{2x}}} \over 3}\); d) \(y = {x^2}{e^x}\).
Giải
a) Đặt \(u = {1 \over x} – 1 \Rightarrow du = – {1 \over {{x^2}}}dx \Rightarrow {{dx} \over {{x^2}}} = – du\)
Do đó \(\int {{1 \over {{x^2}}}} \cos \left( {{1 \over x} – 1} \right)dx = – \int {\cos udu = – \sin u + C = – \sin \left( {{1 \over x} – 1} \right)} + C\)
b) Đặt \(u = 1 + {x^4} \Rightarrow du = 4{x^3}dx \Rightarrow {x^3}dx = {{du} \over 4}\)
\(\int {{x^3}{{\left( {1 + {x^4}} \right)}^3}dx = {1 \over 4}\int {{u^3}du = {{{u^4}} \over {16}} + C = {1 \over {16}}} } {\left( {1 + {x^4}} \right)^4} + C\)
c) Đặt
\(\left\{ \matrix{
u = {x \over 3} \hfill \cr
dv = {e^{2x}}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = {1 \over 3}dx \hfill \cr
v = {1 \over 2}{e^{2x}} \hfill \cr} \right.\)
Suy ra: \(\int {{{x{e^{2x}}} \over 3}dx = {1 \over 6}x{e^{2x}} – {1 \over 6}\int {{e^{2x}}dx = {1 \over 6}x{e^{2x}} – {1 \over {12}}{e^{2x}} + C} } \)
d) Đặt
\(\left\{ \matrix{
u = {x^2} \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = 2xdx \hfill \cr
v = {e^x} \hfill \cr} \right.\)
Suy ra \(\int {{x^2}{e^x}dx = {x^2}{e^x} – 2\int {x{e^x}dx} } \) (1)
Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {e^x} \hfill \cr} \right.\)
Do đó: \(\int {x{e^x}dx = x{e^x} – \int {{e^x}dx = x{e^x} – {e^x} + C} } \)
Từ (1) suy ra \(\int {{x^2}{e^x}dx = {x^2}{e^x} – 2x{e^x} + 2{e^x} + C = {e^x}\left( {{x^2} – 2x + 2} \right) + C} \)
Bài 43
a) \(y = x{e^{ – x}}\); b) \(y = {{\ln x} \over x}\).
Giải
a) Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = {e^{ – x}}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = – {e^{ – x}} \hfill \cr} \right.\)
Suy ra \(\int {x{e^{ – x}}dx = – x{e^{ – x}} + \int {{e^{ – x}}dx = – x{e^{ – x}} – {e^{ – x}} + C = – {e^{ – x}}\left( {x + 1} \right) + C} } \)
b) Đặt \(u = \ln x \Rightarrow du = {{dx} \over x}\)
Do đó \(\int {{{\ln x} \over x}} dx = \int {udu = {{{u^2}} \over 2}} + C = {{{{(\ln x)}^2}} \over 2} + C\)
———————————————————-
Bài 44.
Tìm hàm số \(y = f(x)\) nếu biết \(dy = 12x{\left( {3{x^2} – 1} \right)^3}dx\) và \(f(1) = 3\).
Giải
Ta có \(y = f\left( x \right) = \int {dy = 12\int {x{{\left( {3{x^2} – 1} \right)}^3}dx} } \)
Đặt \(u = 3{x^2} – 1 \Rightarrow du = 6xdx \Rightarrow xdx = {{du} \over 6}\)
Do đó \(f\left( x \right) = 2\int {{u^3}} du = {{{u^4}} \over 2} + C = {1 \over 2}{\left( {3{x^2} – 1} \right)^4} + C\)
Vì \(f\left( 1 \right) = 3\) nên \({1 \over 2}{2^4} + C = 3 \Rightarrow C = – 5\)
Vậy \(f\left( x \right) = {1 \over 2}{\left( {3{x^2} – 1} \right)^4} – 5\)
———————————————-
Bài 45 .
Xác định số b dương để tích phân \(\int\limits_0^b {\left( {x – {x^2}} \right)dx} \) có giá trị lớn nhất.
Giải
Ta có \(\int\limits_0^b {\left( {x – {x^2}} \right)} dx = \left. {\left( {{{{x^2}} \over 2} – {{{x^3}} \over 3}} \right)} \right|_0^b = {{{b^2}} \over 2} – {{{b^3}} \over 3}\)
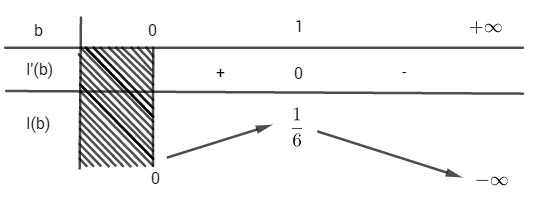
Xét hàm số \(I\left( b \right) = {{{b^2}} \over 2} – {{{b^3}} \over 3}\) với \(b>0\)
ta có
\(\eqalign{
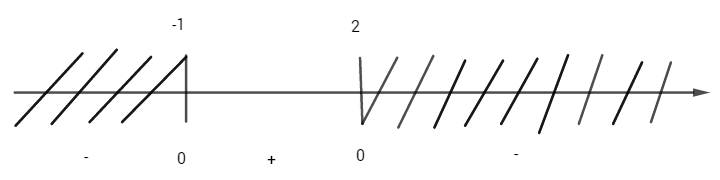
& I’\left( b \right) = b – {b^2} \cr
& I’\left( b \right) = 0 \Leftrightarrow b = 0;b = 1 \cr} \)
Bảng biến thiên
\( I(b)\) đạt giá trị lớn nhất bằng \({1\over 6}\) khi \(b=1\)
——————————————————-
Bài 46 .
Cho biết \(\int\limits_1^9 {f\left( x \right)dx} = – 1,\int\limits_7^9 {f\left( x \right)} dx = 5,\int\limits_7^9 {g\left( x \right)} dx = 4.\)
Hãy tìm:
a) \(\int\limits_1^9 { – 2f\left( x \right)} dx;\) \(b)\,\int\limits_7^9 {\left[ {f\left( x \right) + g\left( x \right)} \right]} dx;\)
\(c)\,\int\limits_7^9 {\left[ {2f\left( x \right) – 3g\left( x \right)} \right]dx;} \) \(d)\,\int\limits_1^7 {f\left( x \right)} dx;\)
Giải
a) \(\int\limits_1^9 { – 2f\left( x \right)} dx = – 2\int\limits_1^9 {f\left( x \right)dx = – 2\left( { – 1} \right)} = 2\)
b) \(\int\limits_7^9 {\left[ {f\left( x \right) + g\left( x \right)} \right]} dx = \int\limits_7^9 {f\left( x \right)} dx + \int\limits_7^9 {g\left( x \right)} dx = 5 + 4 = 9\)
c) \(\int\limits_7^9 {\left[ {2f\left( x \right) – 3g\left( x \right)} \right]dx = } 2\int\limits_7^9 {f\left( x \right)} dx – 3\int\limits_7^9 {g\left( x \right)} dx = 2.5 – 3.4 = – 2\)
d) \(\int\limits_1^7 {f\left( x \right)} dx = \int\limits_1^9 {f\left( x \right)} dx + \int\limits_9^7 {f\left( x \right)} dx = \int\limits_1^9 {f\left( x \right)} dx – \int\limits_7^9 {f\left( x \right)} dx = – 1 – 5 = – 6\)
—————————————————–
Bài 47 .
Cho hàm số f liên tục trên \(\left[ {a;b} \right].\) Tỉ số : \({1 \over {b – a}}\int\limits_a^b {f\left( x \right)} dx\) được gọi là giá trị trung bình của hàm số f trên \(\left[ {a;b} \right]\) và được kí hiệu là \(m\left( f \right)\). Chứng minh rằng tồn tại điểm \(c \in \left[ {a;b} \right]\) sao cho \(m\left( f \right) = f\left( c \right)\)
Giải
Giả sử m và M tương ứng là giá trị bé nhất và lớn nhất của hàm số f trên \(\left[ {a;b} \right]\).
Ta có \(m \le f\left( x \right) \le M\,\,\forall x \in \left[ {a;b} \right]\)
Theo kết quả
\(f(x)>g(x)\) trên đoạn \([a;b]\) thì \(\int\limits_a^b {f(x)} dx > \int\limits_a^b {g(x)dx} \)
Ta có:
\(\eqalign{
& \int\limits_a^b {mdx \le \int\limits_a^b {f\left( x \right)dx} } \le \int\limits_a^b {Mdx} \Rightarrow m\left( {b – a} \right) \le \int\limits_a^b {f\left( x \right)dx \le M\left( {b – a} \right)} \cr
& \Rightarrow m \le {1 \over {b – a}}\int\limits_a^b {f\left( x \right)} dx \le M \cr} \)
Vì \(f\) là hàm liên tục nên tồn tại \(c \in \left[ {a;b} \right]\) để \(f\left( c \right) = {1 \over {b – a}}\int\limits_a^b {f\left( x \right)} dx.\)
———————————————————
Bài 48 .
Giả sử một vật từ trạng thái nghỉ khi \(t=0\) (s) chuyển động thẳng với vận tốc \(v\left( t \right) = t\left( {5 – t} \right)\,\,\,\left( {m/s} \right)\). Tìm quãng đường vật đi được cho tới khi nó dừng lại.
Giải
Ta có
\(v\left( t \right) = 0 \Leftrightarrow \left[ \matrix{
t = 0 \hfill \cr
t = 5 \hfill \cr} \right.\)
Vật dừng lại tại thời điểm \(t=5\). Quãng đường vật đi được là
\(S = \int\limits_0^5 {t\left( {5 – t} \right)} dt = \left. {\left( {{{5{t^2}} \over 2} – {{{t^3}} \over 3}} \right)} \right|_0^5 = {{125} \over 6}\,\,\,\left( m \right)\)
—————————————————-
Bài 49 .
Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt đến vận tốc 6 m/s. từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. biết rằng B đuổi kịp A sau 8 giây ( kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.
Giải
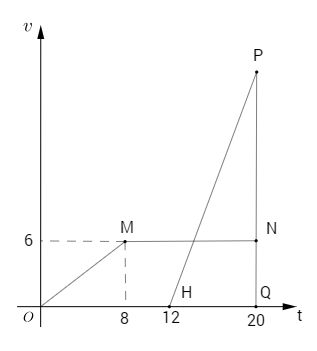
Thời điểm A và B gặp nhau là 20 giây kể từ lúc A xuất phát. Đồ thị của vận tốc của A là đường gấp khúc OMN.
Quãng đường mà A đi được (s = vt ) là diện tích hình thang OMNQ.
\({S_{OMNQ}} = {1 \over 2}\left( {20 + 12} \right).6 = 96\)
Vậy lúc gặp B, A đi được \(96 m\).
Đồ thị vận tốc của B là đường thẳng HP. Vì B xuất phát cùng vị trí với A nên B cũng đi được \(96 m\) . Quãng đường B đi được bằng diện tích tam giác \(HPQ\).
Ta có \({S_{HPQ}} = {1 \over 2}.PQ.HQ \Rightarrow 96 = {1 \over 2}.PQ.8 \Rightarrow PQ = 24.\)
Vậy vận tốc của B tại thời điểm gặp A là \(24\, m/s\).
———————————————————
Bài 50 . Tính các tích phân sau:
\(a)\,\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx;} \) \(b)\,\int\limits_1^2 {x\left( {2{x^2} + 1} \right)} dx;\)
\(c)\,\int\limits_2^3 {\left( {x – 1} \right)} {e^{{x^2} – 2x}}dx.\)
Giải
a) Đặt
\(\left\{ \matrix{
u = {x^2} \hfill \cr
dv = \sin 2xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = 2xdx \hfill \cr
v = – {1 \over 2}\cos 2x \hfill \cr} \right.\)
Do đó \(\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx} = \left. { – {1 \over 2}{x^2}\cos 2x} \right|_0^{{\pi \over 2}} + \int\limits_0^{{\pi \over 2}} {{x^2}\cos 2xdx} \)
\( = {{{\pi ^2}} \over 8} + \int\limits_0^{{\pi \over 2}} {x\cos 2xdx\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)} \)
Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = \cos 2xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {1 \over 2}\sin 2x \hfill \cr} \right.\)
Do đó \(\int\limits_0^{{\pi \over 2}} {x\cos 2xdx\, = \left. {{1 \over 2}x\sin 2x} \right|_0^{{\pi \over 2}}} – {1 \over 2}\int\limits_0^{{\pi \over 2}} {\sin 2xdx} = \left. {{1 \over 4}\cos 2x} \right|_0^{{\pi \over 2}} = – {1 \over 2}\,\,\,\,\,\,\,\,\left( 2 \right)\)
Thay (2) vào (1) ta được: \(\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx = {{{\pi ^2}} \over 8}} – {1 \over 2}.\)
b) Đặt \(u = 2{x^2} + 1 \Rightarrow du = 4xdx \Rightarrow xdx = {{du} \over 4}\)
\(\int\limits_1^2 {x\left( {2{x^2} + 1} \right)dx = {1 \over 4}} \int\limits_3^9 {udu} = \left. {{1 \over 8}{u^2}} \right|_3^9 = 9\)
c) Đặt \(u = {x^2} – 2x \Rightarrow du = 2\left( {x – 1} \right)dx \Rightarrow \left( {x – 1} \right)dx = {{du} \over 2}\)
\(\int\limits_2^3 {\left( {x – 1} \right)} {e^{{x^2} – 2x}}dx = {1 \over 2}\int\limits_0^3 {{e^u}du = } \left. {{1 \over 2}{e^u}} \right|_0^3 = {1 \over 2}\left( {{e^3} – 1} \right).\)
————————————————————
Bài 51 .Tính diện tích các hình phẳng giới hạn bởi:
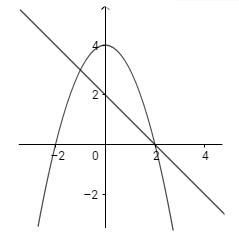
a) Đồ thị các hàm số \(y = 4 – {x^2},y = – x + 2;\)
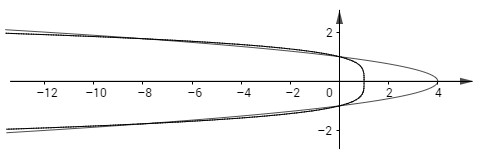
b) Các đường cong có phương trình \(x = 4 – 4{y^2}\) và \(x = 1 – {y^4}\) trong miền \(x\ge0\).
Giải
a) Phương trình hoành độ giao điểm của hai đồ thị là:
\(4 – {x^2} = – x + 2 \Leftrightarrow {x^2} – x – 2 = 0 \Leftrightarrow \left[ \matrix{
x = – 1 \hfill \cr
x = 2 \hfill \cr} \right.\)
Do đó
\(\eqalign{
& S = \int\limits_{ – 1}^2 {\left| {4 – {x^2} – \left( { – x + 2} \right)} \right|} dx = \int\limits_{ – 1}^2 {\left| { – {x^2} + x + 2} \right|} dx \cr
& \,\,\, = \int\limits_{ – 1}^2 {\left( { – {x^2} + x + 2} \right)} dx = \left. {\left( { – {{{x^3}} \over 3} + {{{x^2}} \over 2} + 2x} \right)} \right|_{ – 1}^2 = {9 \over 2} \cr} \)
b) Phương trình tung độ giao điểm của hai đồ thị là
\(4 – 4{y^2} = 1 – {y^4} \Leftrightarrow {y^4} – 4{y^2} + 3 = 0 \Leftrightarrow \left[ \matrix{
{y^2} = 1 \hfill \cr
{y^2} = 3 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
y = \pm 1 \hfill \cr
y = \pm \sqrt 3\; (\text{ loại vì } x<0)\hfill \cr} \right.\)
Diện tích giới hạn hai đồ thị ở phần \(x \ge 0\) là:
\(\eqalign{
& S = \int\limits_{ – 1}^1 {\left[ {4 – 4{y^2} – \left( {1 – {y^4}} \right)} \right]} dy \cr
& \,\,\, = \int\limits_{ – 1}^1 {\left( {{y^4} – 4{y^2} + 3} \right)} dy \cr
& \,\, = \left. {\left( {{{{y^5}} \over 5} – {4 \over 3}{y^3} + 3y} \right)} \right|_{ – 1}^1 = 2.{{28} \over {15}} = {{56} \over {15}} \cr} \)
——————————————————-
Bài 52 . Tính diện tích của các hình phẳng giới hạn bởi:
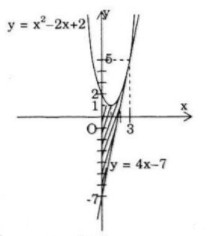
a) Parabol \(y = {x^2} – 2x + 2,\) tiếp tuyến của nó tại điểm \(M(3;5)\) và trục tung;
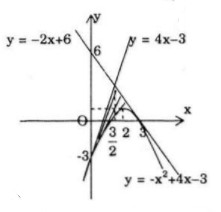
b) Parabol \(y = – {x^2} + 4x – 3\) và các tiếp tuyến của nó tại các điểm \(A(0;-3)\) và \(B(3;0)\)
Giải
a)
Ta có \(y’ = 2x – 2 \Rightarrow y’\left( 3 \right) = 4.\)
Phương trình tiếp tuyến với parabol tại M(3;5) là:
\(y – 5 = 4\left( {x – 3} \right) \Leftrightarrow y = 4x – 7\)
Gọi S là diện tích cần tìm, ta có :
\(\eqalign{
& S = \int\limits_0^3 {\left( {{x^2} – 2x + 2 – 4x + 7} \right)} dx \cr
& \,\,\, = \int\limits_0^3 {\left( {{x^2} – 6x + 9} \right)} dx = \int\limits_0^3 {{{\left( {x – 3} \right)}^2}dx} \cr
& \,\,\, = \left. {{1 \over 3}{{\left( {x – 3} \right)}^3}} \right|_0^3 = 9. \cr} \)
b)
Ta có \(y’ = – 2x + 4 \Rightarrow y’\left( 0 \right) = 4;y’\left( 3 \right) = – 2\)
Phương trình tiếp tuyến tại \(A(0;3)\) là :
\(y + 3 = 4\left( {x – 0} \right) \Leftrightarrow y = 4x – 3\)
Phương trình tiếp tuyến tại \(B(3;0)\) là :
\(y = – 2\left( {x – 3} \right) \Leftrightarrow y = – 2x + 6\)
Giao điểm của hai tiếp tuyến là \(C\left( {{3 \over 2};3} \right).\) kí hiệu \({A_1}\) và \({A_2}\) là tam giác cong \(ACD\) Và \(BCD\). Ta có :
\(S\left( {{A_1}} \right) = \int\limits_0^{{3 \over 2}} {\left( {4x – 3 + {x^2} – 4x + 3} \right)} dx = \int\limits_0^{{3 \over 2}} {{x^2}dx = \left. {{{{x^3}} \over 3}} \right|_0^{{3 \over 2}}} = {9 \over 8}\)
\(S\left( {{A_2}} \right) = \int\limits_{{3 \over 2}}^3 {\left( { – 2x + 6 + {x^2} – 4x + 3} \right)} dx = \int\limits_{{3 \over 2}}^3 {{{\left( {x – 3} \right)}^2}dx = } \left. {{1 \over 3}{{\left( {x – 3} \right)}^3}} \right|_{{3 \over 2}}^3 = {9 \over 8}\)
Vậy \(S = S\left( {{A_1}} \right) + S\left( {{A_2}} \right) = {9 \over 8} + {9 \over 8} = {9 \over 4}\)
—————————————————
Bài 53 .
Tính thể tích của vật thể nằm giữa hai mặt phẳng \(x=0\) và \(x=2\), biết rằng thiết diện của vật thể bị cắt bơi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \(\left( {0 \le x \le 2} \right)\) là một nửa hình tròn đường kính \(\sqrt 5 {x^2}\).
Giải
Diện tích của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \(x\) là:
\(S\left( x \right) = {1 \over 2}\pi {\left( {{{\sqrt 5 } \over 2}{x^2}} \right)^2} = {1 \over 2}.{{5\pi } \over 4}{x^4} = {{5\pi } \over 8}{x^4}\)
Vậy thể tích của vật thể là : \(V = \int\limits_0^2 {S\left( x \right)dx = {{5\pi } \over 8}} \int\limits_0^2 {{x^4}dx} = \left. {{{5\pi } \over 8}.{{{x^5}} \over 5}} \right|_0^2 = 4\pi .\)
————————————————————-
Bài 54 .
Xét hình phẳng giới hạn bởi đường hypebol \(y = {2 \over x}\) và các đường thẳng \(y=1\) , \(y = 4,x = 0.\) Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng đó quanh trục tung.
Giải
Ta có \(y = {2 \over x} \Leftrightarrow x = {2 \over y}\)
Thể tích cần tìm là : \(V = \pi \int\limits_1^4 {\left( {{2 \over y}} \right)^2} dy = 4\pi \int\limits_1^4 {{{dy} \over {{y^2}}}} = \left. {4\pi \left( {{-1 \over y}} \right)} \right|_1^4 = 3\pi \)
—————————————————————–
Bài 55.
Cho hình phẳng A được giới hạn bởi đồ thị hàm số : \(y = \sqrt {\cos x} \left( {0 \le x \le {\pi \over 2}} \right)\,\) và hai trục tọa độ. Tính thể tích khối tròn xoay tọa thành khi quay hình đó quay trục tung.
Giải
Hoành độ giao điểm của hàm số \(y = \sqrt {\cos x} \left( {0 \le x \le {\pi \over 2}} \right)\,\)với trục hoành là nghiệm phương trình :
\(\left\{ \matrix{
\sqrt {\cos x} = 0 \hfill \cr
0 \le x \le {\pi \over 2} \hfill \cr} \right. \Leftrightarrow x = {\pi \over 2}\)
Vậy thể tích cần tìm là : \(V = \pi \int\limits_0^{{\pi \over 2}} {\cos xdx = \left. {\pi {\mathop{\rm s}\nolimits} {\rm{inx}}} \right|_0^{{\pi \over 2}}} = \pi \)
————————————————————–
Bài 56 .
Cho hình phẳng A được giới hạn bởi đường cong có phương trình \(x\left( {y + 1} \right) = 2\) và các đường thẳng \(x = 0,y = 0,y = 3.\) tính thể tích khối tròn xoay tạo được khi quay A quanh trục tung.
Giải
Đường cong có phương trình là \(x = {2 \over {y + 1}}.\)
Vậy thể tích cần tìm là: \(V = \pi \int\limits_0^3 {{4 \over {{{\left( {y + 1} \right)}^2}}}} dy = \left. {4\pi \left( { – {1 \over {y + 1}}} \right)} \right|_0^3 = 3\pi \)
—————————————————————–
Bài 58.
Cho hình phẳng A được giới hạn bởi đường cong có phương trình \(y = {x^{{1 \over 2}}}{e^{{x \over 2}}}\) và các đường thẳng \(x = 1,x = 2,y = 0.\) Tính thể tích khối tròn xoay tạo thành khi quay A quanh trục hoành.
Giải
Thể tích cần tìm là: \(V = \pi \int\limits_1^2 {x.{e^x}} dx\)
Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {e^x} \hfill \cr} \right.\)
Do đó \(V = \pi \left( {\left. {x{e^x}} \right|_1^2 – \int\limits_1^2 {{e^x}dx} } \right) = \pi \left( {2{e^2} – e – {e^2} + e} \right) = \pi {e^2}\)
———————————————————
Bài 59 .
Cho hình phẳng A được giới hạn bởi đường cong có phương trình \({y^2} = {x^3}\) và các đường thẳng \(y = 0,x = 1.\) Tính thể tích khối tròn xoay tạo được khi quay A
a) Quanh trục hoành; b) Quanh trục tung.
Giải
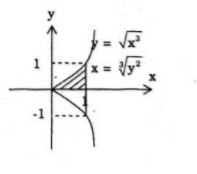
a) Ta có \(y = \sqrt {{x^3}} \,\,\left( {y \ge 0} \right)\)
Thể tích cần tìm là: \(V = \pi \int\limits_0^1 {{x^3}dx = \left. {{{\pi {x^4}} \over 4}} \right|} _0^1 = {\pi \over 4}\)
b) Ta có \(x = \root 3 \of {{y^2}} \)
Thể tích cần tìm là: \(V = \pi \int\limits_0^1 {\left( {{1^2}-\root 3 \of {{y^4}} } \right)} dy = \left. {\pi \left( {y – {3 \over 7}{y^{{7 \over 3}}}} \right)} \right|_0^1 = {{4\pi } \over 7}.\)
—————————————————–
Bài 57 .
Cho hình phẳng A được giới hạn bởi đường cong có phương trình \(x – {y^2} = 0\) và các đường thẳng \(y = 2,x = 0\). Tính thể tích khối tròn xoay tạo thành khi quay A.
a) Quanh trục hoành; b) quanh trục tung
Giải
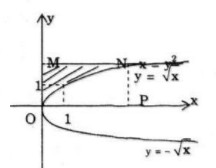
a) Hoành độ giao điểm của đường cong \(y=\sqrt x\) và \(y=2\) là:
\(\sqrt x=2\Rightarrow x=4\)
Thể tích khối tròn xoay tạo thành khi quay A quanh \(Ox\) là:
\(V = \pi \int\limits_0^4 {\left( {{2^2} – x} \right)} dx = \left. {\pi \left( {4x – {{{x^2}} \over 2}} \right)} \right|_0^4 = 8\pi \)
b) Thể tích khối tròn xoay tạo thành khi quay A quanh \(Oy\) là:
\(V = \pi \int\limits_0^2 {{y^4}dy} = \left. {{\pi \over 5}{y^5}} \right|_0^2 = {{32\pi } \over 5}\)

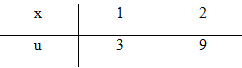
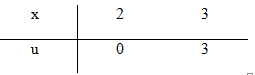
Trả lời