Giải bài 1 trang 18 SGK Hình học 12.
Đề bài
Cắt bìa theo mẫu dưới đây (h.1.23), gấp theo đường kẻ, rồi dán các mép lại để được các hình tứ diện đều, hình lập phương và hình bát diện đều.
Phương pháp giải
Dùng một miếng bìa, kẻ các đường kẻ như hình mẫu rồi gấp tấm bìa theo các đường đó sẽ tạo thành các hình tứ diện đều, hình lập phương và bát diện đều.
Lời giải chi tiết
Đây là bài tập thủ công, học sinh tự thực hành.
Giải bài 2 trang 18 SGK Hình học 12.
Đề bài
Cho hình lập phương \((H)\). Gọi \((H’)\) là hình bát diện đều có các đỉnh là tâm các mặt của \((H)\). Tính tỉ số diện tích toàn phần của \((H)\) và \((H’)\).
+) Bát diện đều là khối đa diện gồm 8 mặt là 8 tam giác đều.
+) Diện tích toàn phần của hình bát diện đều = 8. diện tích 1 mặt.
Lời giải chi tiết
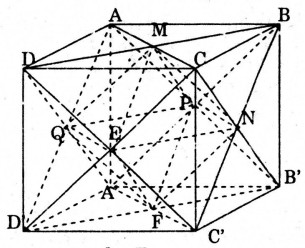
Giả sử khối lập phương có cạnh bằng \(a\). Khi đó diện tích toàn phần của nó là: \(S_1 = 6. a^2\)
Gọi \(M\) là tâm của hình vuông \(AMCD\); \(Q\) là tâm hình vuông \(ADD’A’\); \(P\) là tâm hình vuông \(ABB’A’\); \(N\) là tâm hình vuông \(BCC’B’\); \(E\) là tâm hình vuông \(DCC’D’\) và \(F\) là tâm hình vuông \(A’B’C’D’\).
Xét bát diện đều thu được, khi đó diện tích toàn phần của nó là \(8\) lần diện tích tam giác đều \(MQE\) (hình vẽ)
Xét tam giác \(ACD’\), ta có \(M, Q\) lần lượt là trung điểm của \(AC\) và \(AD’\) nên \(MQ\) là đường trung bình của tam giác \(ACD’\), do đó \(MQ = {1 \over 2}C{\rm{D}}’ = {1 \over 2}\sqrt 2a \)
Ta có \({S_{AMQE}} = {1 \over 2}{\left( {{1 \over 2}\sqrt 2a } \right)^2}.{{\sqrt 3 } \over 2} = {1 \over 8}{a^2}\sqrt 3 \)
Diện tích xung quanh của bát diện đều là: \({S_2} = 8.{1 \over 8}.{a^2}\sqrt 3 = {a^2}\sqrt 3 \)
Do đó: \({{{S_1}} \over {{S_2}}} = {{6{{\rm{a}}^2}} \over {a\sqrt 3 }} = 2\sqrt 3 \)
Giải bài 3 trang 18 SGK Hình học 12.
Đề bài
Chứng minh rằng tâm của các mặt của hình tứ diện đều là các đỉnh của một hình tứ diện đều.
+) Sử dụng tính chất đường trung tuyến của tam giác và định lý Ta-lét để làm bài toán.
Lời giải chi tiết
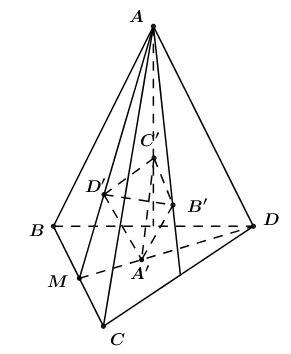
Gọi \(A’, B’, C’, D’\) lần lượt là trọng tâm của các tam giác đều \(BCD, ACD, ABD, ABC\).
Gọi \(M\) là trung điểm \(BC\):
Ta có: \({{M{\rm{D}}’} \over {MA}} = {{MA’} \over {M{\rm{D}}}} = {1 \over 3}\) (tính chất đường trung tuyến).
\( \Rightarrow A’D’//A{\rm{D}}\) (định lý Ta-lét).
và \(A’D’ = {1 \over 3}A{\rm{D}} = {a \over 3}\)
Tương tự \(A’B’ = B’C’ = C’A’ = B’D’ = C’D’ = {a \over 3}\)
Vậy \(A’B’C’D’\) là tứ diện đều
Giải bài 4 trang 18 SGK Hình học 12.
Đề bài
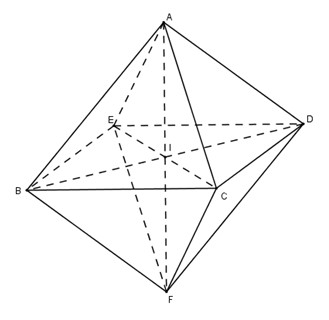
Cho hình bát diện đều \(ABCDEF\)
Chứng minh rằng :
a) Các đoạn thẳng \(AF, BD\) và \(CE\) đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
b) \(ABFD, AEFC\) và \(BCDE\) là những hình vuông.
+) Sử dụng tính chất của mặt phẳng trung trực.
+) Dấu hiệu nhân biết hình vuông: Hình thoi có hai đường chéo bằng nhau là hình vuông.
Lời giải chi tiết
a) Do \(B, C, D, E\) cách đều \(A\) và \(F\) nên chúng đồng phẳng (cùng thuộc mặt phẳng trung trực của \(AF\)).
Tương tự, \(A, B, F, D\) đồng phẳng và \(A, C, F, E\) đồng phẳng
Gọi \(I\) là giao của \((AF)\) với \((BCDE)\). Khi đó \(B, I, D\) là những điểm chung của hai mặt phẳng \((BCDE)\) và \((ABFD)\) nên chúng thẳng hàng. Tương tự, \(E, I , C\) thẳng hàng.
Vậy \(AF, BD, CE\) đồng quy tại \(I\).
Vì \(BCDE\) là hình thoi nên \(EC\) vuông góc với \(BC\) và cắt \(BC\) tại \(I\) là trung điểm của mỗi đường. \(I\) là trung điểm của \(AF\) và \(AF\) vuông góc với \(BD\) và \(EC\), do đó các đoạn thẳng \(AF, BD\), và \(CE\) đôi một vuông góc với nhau cắt nhau tại trung điểm của chúng.
b) Ta có tứ giác \(DCDE\) là hình thoi.
Do \(AI\) vuông góc \((BCDE)\) và \(AB = AC =AD = AE\) nên \(IB = IC= ID = IE\).
Từ đó suy ra hình thoi \(BCDE\) là hình vuông. Tương tự \(ABFD, AEFC\) là những hình vuông.
======================




Trả lời