Câu hỏi:
Cho số phức z thỏa mãn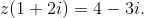 
Tìm số phức 
liên hợp của z.
- A. \(\overline z = – \frac{2}{5} – \frac{{11}}{5}i\)
- B. \(\overline z = \frac{2}{5} – \frac{{11}}{5}i\)
- C. \(\overline z = \frac{2}{5} + \frac{{11}}{5}i\)
- D. \(\overline z = – \frac{2}{5} + \frac{{11}}{5}i\)
Đáp án đúng: D
Ta có \(z = \frac{{4 – 3i}}{{1 + 2i}} = \frac{{(4 – 3i)(1 – 2i)}}{{(1 + 2i)(1 – 2i)}} = \frac{{4 – 8i – 3i + 6{i^2}}}{{1 – 4{i^2}}} = – \frac{2}{5} – \frac{{11}}{5}i\)
\(\Rightarrow \overline z = – \frac{2}{5} + \frac{{11}}{5}i.\)
Trả lời